Plantilla:Perímetros y áreas
De Wikipedia
| Revisión de 19:55 16 nov 2016 Coordinador (Discusión | contribuciones) (→Polígonos regulares) ← Ir a diferencia anterior |
Revisión de 20:23 16 nov 2016 Coordinador (Discusión | contribuciones) (→Círculo) Ir a siguiente diferencia → |
||
| Línea 43: | Línea 43: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Círculo''|cuerpo= | + | {{Geogebra_enlace |
| - | {{ai_cuerpo | + | |descripcion=En esta escena podrás deducir la fórmula de la longitud de la circunferencia de forma aproximada. |
| - | |enunciado='''Actividad 1:''' Comprobación de la fórmula de la longitud de la circunferencia. | + | |enlace=[https://ggbm.at/DHf8DHWx Longitud de la circunferencia] |
| - | {{p}} | + | |
| - | |actividad=Desliza el punto verde y observa | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/longitud_circunferencia.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/longitud_circunferencia.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividad interactiva: ''Círculo''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| |enunciado='''Actividad 2:''' Aproximación a la fórmula del área del círculo. | |enunciado='''Actividad 2:''' Aproximación a la fórmula del área del círculo. | ||
Revisión de 20:23 16 nov 2016
Tabla de contenidos |
Cuadrado
Área y perímetro del cuadrado. Ejemplo.
Calcula el área de un cuadrado de 1.2 cm de lado.
Calcula el área de un cuadrado cuya diagonal mide 20 cm.
Calcula el área de un cuadrado inscrito en una circunferencia de radio 1 cm.
En esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del cuadrado; en la segunda podrás calcular el área y el perímetro del cuadrado.
Ejercicios de autoevaluación sobre áreas de cuadrados.
|
Actividad: El cuadrado
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Rectángulo
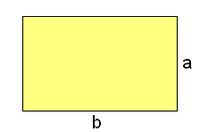
Área y perímetro del rectángulo. Ejemplo.
Área del rectángulo. Ejemplo.
Demostración de la fórmula del área del rectángulo.
Calcula el área en metros cuadrados de una finca que tiene forma rectangular con un lado de 2 km y una diagonal de 6 km.
Determinar el área de un rectángulo que tiene 60 cm de perímetro, si la razón entre sus lados es 3:2.
Carlos construyó una mesa rectangular con un perímetro de 20 pies y un área de 24 pies cuadrados. Sabiendo que la mesa es más larga que ancha y que los lados son números enteros, calcula por tanteo las dimensiones de la mesa.
Juan construyó un corral rectangular de 21 pies de largo y 78 pies de perímetro. ¿Cuál es el ancho del corral?
En esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del rectángulo; en la segunda podrás calcular el área y el perímetro del rectángulo.
Ejercicios de autoevaluación sobre áreas de rectángulos.
Problemas verbales de área y perímetro de rectángulos.
|
Actividad: El rectángulo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Paralelogramo
Área y perímetro del romboide. Ejemplos.
Área del paralelogramo. Ejemplo.
Demostración de la fórmula del área del romboide.
Halla el área y el perímetro de un romboide de lados 20 cm y 13 cm, siendo la altura de 12 cm..
Halla el área y el perímetro de un romboide a partir de la información que aparece dibujada.
En esta escena podrás deducir la fórmula del área del romboide y practicar con ella.
Ejercicios de autoevaluación sobre áreas de romboides.
|
Actividad: El romboide
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Rombo
Ejemplo de cálculo del área y del perímetro de un rombo.
Demostración de la fórmula del área de un rombo.
Nota: Hay un error al comienzo del video al enunciar la fórmula (dice "semiproducto de las longitudes de los lados" y debería decir "semiproducto de las longitudes de las diagonales"), aunque luego el resto de la demostración es correcta.
Halla el área y el perímetro de un rombo cuyas diagonales miden 36 cm y 24 cm.
El lado de un rombo mide 20 m y una de las diagonales 32 m. Calcula su área.
Calcula el perímetro de un rombo cuyas diagonales miden 5 m y 6 m, respectivamente.
Calcula el área y el perímetro de un rombo cuyas diagonales miden 10 y 14 cm, respectivamente.
En esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del rombo; en la segunda podrás calcular el área y el perímetro del rombo.
Ejercicios de autoevaluación sobre áreas de rombos.
|
Actividad: El rombo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Triángulo
|
|
Videotutorial que condensa todo lo que vamos a ver sobre medidas en los triángulos.
Fórmula general y tres casos prácticos de cómo calcular el área de un triángulo.
Deducción del área de un triángulo.
Deduciendo la fórmula del área del triángulo.
Demostración de área del triángulo.
Calcula la altura de un triángulo de 34 cm2 de área y 10 cm de base.
El área de un triángulo isósceles es de 24 dm2. Si sabemos que la altura relativa al lado desigual es de 100 cm, ¿cuántos cm mide este lado?
Calcula el área de un triángulo equilátero de 7 cm de lado.
Calcula el la altura, el área y el perímetro de un triángulo isósceles de 8 cm de base y cuyos lados iguales miden 7 cm.
Calcula el área de un triángulo equilátero de 36 m de perímetro.
En esta escena podrás deducir la fórmula del área del triángulo.
Ejercicios de autoevaluación sobre el área y el perímetro de triángulos.
Actividades sobre el área del triángulo.
Ejercicios de autoevaluación sobre el área del triángulo.
Ejercicios de autoevaluación sobre el área del triángulo.
Ejercicios de autoevaluación sobre el área del triángulo.
Ejercicios de autoevaluación sobre el área del triángulo.
Fórmula de Herón
Nota: El nivel de esta demostración corresponde a 1º de Bachillerato.
Una demostración moderna, que emplea álgebra y trigonometría (bastante distinta a la que dio Herón en su libro), podría ser la siguiente.
Supongamos un triángulo de lados  ,
,  ,
,  , cuyos ángulos opuestos a cada uno de esos lados son
, cuyos ángulos opuestos a cada uno de esos lados son 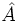 ,
, 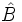 ,
, 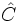 .
.
Por el teorema del coseno, tenemos que:
Por la relación fundamental de la trigonometría, tenemos que:
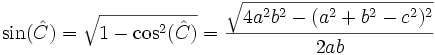 .
.
La altura de un triángulo de base  tiene una longitud
tiene una longitud 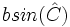 , por tanto siguiendo con la demostración
, por tanto siguiendo con la demostración
En esta escena podrás calcular el área de un triángulo mediante la fórmula de Herón.
Determinar el área y el perímetro de un triángulo cuyos lados miden 3, 4 y 5.
Determinar el área y el perímetro de un triángulo cuyos lados miden 4.4, 6.7 y 9.3.
Determinar el área y el perímetro de un triángulo rectángulo cuyos catetos miden 24 cm y 7 cm.
|
Actividad: El triángulo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
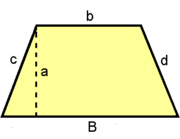
Trapecio
El trapecio y su área. Ejemplo.
Demostración de la fórmula del área de un trapecio.
Halla el área de un trapecio isósceles que tiene 9 cm de base menor, 12 cm de base mayor y 3 cm de altura.
Halla el área de un trapecio isósceles que tiene 8 cm de base menor, 12 cm de base mayor y 5 cm de lados no paralelos.
Halla el área y el perímetro de un trapecio isósceles que tiene 9 cm de base menor, 15 cm de base mayor y 5 cm de lados no paralelos.
Las bases de un trapecio rectángulo miden 6 cm y 2 cm, respectivamente. La altura mide 3 cm. Calcula su perímetro.
Las bases de un trapecio rectángulo miden 4 cm y 7 cm, y su altura 4 cm. Halla su perímetro.
Las bases de un trapecio rectángulo miden 8 cm y 6 cm, y su altura 5 cm. Halla su perímetro y su área.
Esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del trapecio; en la segunda podrás aplicar dicha fórmula en un caso práctico.
En esta escena podrás deducir la fórmula del área del trapecio de otra manera. Además podrás realizar el cálculo del área en una actividad.
Ejercicios de autoevaluación sobre áreas de trapecios.
Ejercicio resuelto: Área del trapecio
Halla el área de un trapecio isósceles cuyas bases miden 37 cm y 55 cm, y el lado oblicuo, 14 cm.
Utilizando el teorema de Pitágoras se halla la altura a=10.7 cm. A continuación se aplica la fórmula para hallar el área.
Solución: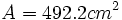
|
Actividad: El trapecio
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Polígonos regulares
Áreas y perímetros en polígonos regulares.
Áreas de polígonos regulares. Ejemplo.
Áreas de polígonos regulares. Ejemplo
Áreas de polígonos regulares.
Halla el área de un pentágono regular de 2.5 cm de lado y 2.16 cm de apotema.
Halla el área de un hexágono regular de 9 cm de lado.
Halla el área de un hexágono regular inscrito en una circunferencia de 6 dm de radio.
La base de un edificio con forma de pentágono regular tiene una superficie de 1000 m2. Si la distancia del centro del edificio a una de las puertas, situada en el punto medio de uno de sus lados, es de 12 m, ¿Cuánto mide cada lado del edificio?
Calcula el área de una hexágono regular de 10 cm de lado.
¿Cuántas baldosas con forma de hexágono regular de 80 cm de lado se necesitan para embaldosar una habitación de 13 m de largo por 9.4 m de ancho?
Calcula el lado de un octógono regular de 4 cm de apotema y 110 cm2 de área.
En esta escena podrás ver cómo se deduce el área de un polígono regular.
En esta escena podrás calcular el área y el perímetro de algunos polígonos regulares.
Actividad sobre áreas de polígonos regulares.
En esta escena podrás estudiar los elementos de un polígono regular: lados, diagonales, apotema y ángulos. También podrás calcular el perímetro y el área. El número de lados puede elegirse entre 3 y 20.
Actividades guiadas sobre áreas de polígonos regulares.
Ejercicios de autoevaluación sobre áreas de polígonos regulares.
Ejercicios de autoevaluación sobre áreas de polígonos regulares.
|
Actividad: Polígonos regulares
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Círculo
En esta escena podrás deducir la fórmula de la longitud de la circunferencia de forma aproximada.
|
Actividad interactiva: Círculo Actividad 2: Aproximación a la fórmula del área del círculo.
Actividad 3: En un círculo de radio 1,71 cm, halla su área y la longitud de su circunferencia.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: Calculo del área y del perímetro de un círculo.
|
|
Actividad: El círculo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Corona circular
|
Actividad interactiva: Corona circular
1. Halla el área de una corona circular cuyos círculos tienen de radio 2 cm y 1,37 cm, respectivamente.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: Calculo del área de una corona circular
(Mueve el punto azul para modificar el radio pequeño)
|
Sector circular
La fórmula del área del sector circular se obtiene a partir de la del área del círculo, aplicando una regla de tres.
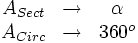
Despejando el área del sector:
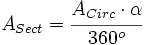
de donde, sustituyendo el área del círculo por su valor, 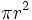 , se obtiene la fórmula.
, se obtiene la fórmula.
Lo mismo ocurre con la de la longitud del arco, que se obtiene a partir de la de la longitud de la circunferencia, también mediante una regla de tres.
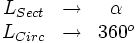
Despejando la longitud del sector:
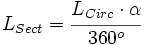
de donde, sustituyendo la longitud de la circunferencia por su valor, 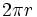 , se obtiene la fórmula.
, se obtiene la fórmula.
|
Actividad interactiva: Sector circular
1. En un círculo de radio 1,80 cm, halla el área de un sector circular de 60º y la longitud de su arco.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: Calculo del área de un sector circular
(Mueve el punto B para modificar el ángulo) |
|
Actividad: El sector circular
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|

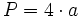
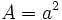

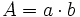

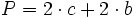
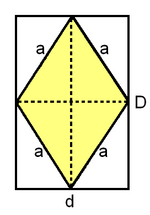
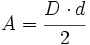
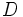 : diagonal mayor.
: diagonal mayor.
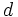 : diagonal menor.
: diagonal menor.

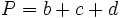
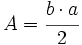
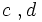 : lados.
: lados.
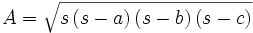
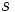 es el semiperímetro:
es el semiperímetro: 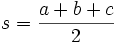 .
.
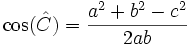
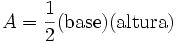
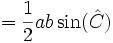
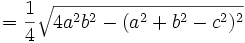
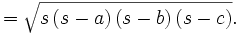
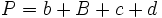
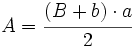
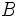 : base mayor.
: base mayor.
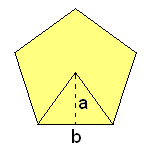
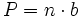
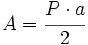
 : número de lados.
: número de lados.
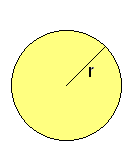
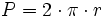
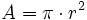
 : radio.
: radio.
 : número Pi = 3,14159...
: número Pi = 3,14159...
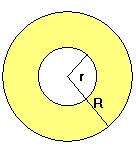
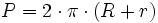
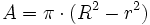
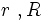 : radios respectivos.
: radios respectivos.
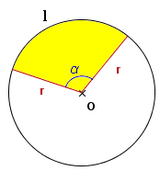
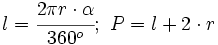
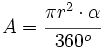
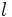 : arco.
: arco.
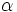 : ángulo (en grados sexagesimales).
: ángulo (en grados sexagesimales).

