Plantilla:Función inversa (1ºBach)
De Wikipedia
| Revisión de 10:09 13 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:12 13 dic 2016 Coordinador (Discusión | contribuciones) (→Función inversa o recíproca) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| |texto= | |texto= | ||
| - | Sea <math>f\;</math> una función real [[Función inyectiva|inyectiva]], cuyo dominio sea el conjunto <math>X\;</math> y cuya imagen sea el conjunto <math>Y\;</math>. Entonces, la '''función recíproca o inversa''' de <math>f\;</math>, denotada <math>f^{-1}\;</math>, es la función de dominio <math>Y\;</math> e imagen <math>X\;</math> definida por la siguiente regla: | + | Sea <math>f\;</math> una función real [[Función biyectiva|biyectiva]], cuyo dominio sea el conjunto <math>X\;</math> y cuya imagen sea el conjunto <math>Y\;</math>. Entonces, la '''función recíproca o inversa''' de <math>f\;</math>, denotada <math>f^{-1}\;</math>, es la función de dominio <math>Y\;</math> e imagen <math>X\;</math> definida por la siguiente regla: |
| <center><math>f(x) = y\Leftrightarrow{}f^{-1}(y) = x \,\!</math></center> | <center><math>f(x) = y\Leftrightarrow{}f^{-1}(y) = x \,\!</math></center> | ||
Revisión de 10:12 13 dic 2016
Función inversa o recíproca
Si  es una función que lleva elementos de es una función que lleva elementos de 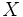 en elementos de en elementos de 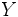 , en ciertas condiciones será posible definir la aplicación , en ciertas condiciones será posible definir la aplicación 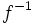 que realice el camino de vuelta de que realice el camino de vuelta de 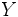 a a 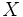 . En ese caso diremos que . En ese caso diremos que 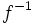 es la función inversa o recíproca de es la función inversa o recíproca de  . Formalmente: . Formalmente:
Sea  Propiedades Sea
donde Demostración: |
|
Actividad Interactiva: Función inversa
Actividad 1. Representación gráfica de una función
 y de su inversa y de su inversa  . .Actividad: En esta escena tienes la gráfica de la función 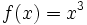 (en verde) y la de (en verde) y la de ![f^{-1}(x)=\sqrt[3]{x}](/wikipedia/images/math/7/8/7/787a4594029c72e736448583d9724079.png) (en amarillo). Observa que son simétricas respecto de la bisectriz del primer cuadrante, la recta (en amarillo). Observa que son simétricas respecto de la bisectriz del primer cuadrante, la recta 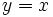 (en rojo). (en rojo).
Prueba a cambiar también la función |
Ejemplo: Función inversa
Halla la función inversa de la función 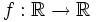 definida por
definida por  :
:
Como la función  no es inyectiva, no podemos calcular su inversa. No obstante, podemos descomponerla en dos trozos que si sean funciones inyectivas por separado y alos que si podamos calcular su inversa:
no es inyectiva, no podemos calcular su inversa. No obstante, podemos descomponerla en dos trozos que si sean funciones inyectivas por separado y alos que si podamos calcular su inversa:
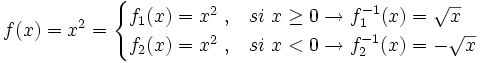
En la siguiente escena puedes ver  (en verde),
(en verde), 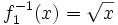 (en amarillo), y
(en amarillo), y 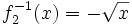 (en turquesa):
(en turquesa):
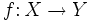 una función y
una función y 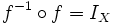

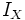 e
e 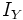 son las
son las