Números naturales
De Wikipedia
| Revisión de 11:50 27 may 2007 Coordinador (Discusión | contribuciones) (→Jerarquía de las operaciones) ← Ir a diferencia anterior |
Revisión de 21:09 25 jun 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Definición== | + | ==Números naturales== |
| {{Caja Amarilla|texto=El conjunto de los '''números naturales''' es <math>\mathbb{N}=\left \lbrace 0,\ 1 ,\ 2,\ 3, \cdots \right \rbrace</math>. Son infinitos y sirven para contar ('''números cardinales''': 1, 2, 3, ...) o para ordenar ('''números ordinales''': 1º, 2º, 3º, ...).}} | {{Caja Amarilla|texto=El conjunto de los '''números naturales''' es <math>\mathbb{N}=\left \lbrace 0,\ 1 ,\ 2,\ 3, \cdots \right \rbrace</math>. Son infinitos y sirven para contar ('''números cardinales''': 1, 2, 3, ...) o para ordenar ('''números ordinales''': 1º, 2º, 3º, ...).}} | ||
| Línea 13: | Línea 13: | ||
| {{p}} | {{p}} | ||
| - | ==Operaciones== | + | ==Operaciones con números naturales== |
| - | ===Suma y multiplicación=== | + | ===Suma y multiplicación de números naturales=== |
| La '''suma''' (o adición) y la '''multiplicación''' (o producto) de dos números naturales es otro número natural. Por eso se dice que estas dos operaciones son '''[http://es.wikipedia.org/wiki/Operaci%C3%B3n_matem%C3%A1tica leyes de composición interna]'''. | La '''suma''' (o adición) y la '''multiplicación''' (o producto) de dos números naturales es otro número natural. Por eso se dice que estas dos operaciones son '''[http://es.wikipedia.org/wiki/Operaci%C3%B3n_matem%C3%A1tica leyes de composición interna]'''. | ||
| {{p}} | {{p}} | ||
| - | ===Resta y división=== | + | ===Resta y división de números naturales=== |
| La '''resta''' (o substracción)y la '''división''' (o cociente) de dos números naturales no siempre es otro número natural. Por eso se dice que estas dos operaciones son '''[http://es.wikipedia.org/wiki/Operaci%C3%B3n_matem%C3%A1tica leyes de composición externa]'''. | La '''resta''' (o substracción)y la '''división''' (o cociente) de dos números naturales no siempre es otro número natural. Por eso se dice que estas dos operaciones son '''[http://es.wikipedia.org/wiki/Operaci%C3%B3n_matem%C3%A1tica leyes de composición externa]'''. | ||
| {{p}} | {{p}} | ||
| - | ===Propiedades=== | + | ===Propiedades de la suma y el producto de números naturales=== |
| La suma y la multiplicación cumplen las siguientes propiedades: | La suma y la multiplicación cumplen las siguientes propiedades: | ||
| {{Caja Amarilla|texto= | {{Caja Amarilla|texto= | ||
| Línea 45: | Línea 45: | ||
| {{p}} | {{p}} | ||
| - | ===División=== | + | ===División de números naturales=== |
| La '''división''' puede verse como un reparto de un número de elementos ('''dividendo''') en un número de partes iguales ('''divisor'''), que da como resultado el número de elementos que corresponden a cada parte ('''cociente''') y un posible número de elementos sobrantes ('''resto'''). Si el resto es cero la división se llama '''exacta''', si no, se llama '''entera'''. | La '''división''' puede verse como un reparto de un número de elementos ('''dividendo''') en un número de partes iguales ('''divisor'''), que da como resultado el número de elementos que corresponden a cada parte ('''cociente''') y un posible número de elementos sobrantes ('''resto'''). Si el resto es cero la división se llama '''exacta''', si no, se llama '''entera'''. | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| Línea 56: | Línea 56: | ||
| {{p}} | {{p}} | ||
| - | ===Potenciación=== | + | ===Potenciación de números naturales=== |
| {{Caja Amarilla|texto= | {{Caja Amarilla|texto= | ||
| Una potencia de '''base''' ''a'' y '''exponente''' ''n'' consiste en multiplicar ''n'' veces la base ''a''. | Una potencia de '''base''' ''a'' y '''exponente''' ''n'' consiste en multiplicar ''n'' veces la base ''a''. | ||
| Línea 100: | Línea 100: | ||
| }} | }} | ||
| - | ====Propiedades==== | + | ====Propiedades de las potencias de números naturales==== |
| {{Caja Amarilla|texto=<center><math>a^0=1\,\!</math>{{b}}{{b}}<math>a^m \cdot a^n=a^{n+m}</math>{{b}}{{b}}<math>\cfrac{a^m}{a^n}=a^{m-n}\,\!</math>{{b}}{{b}}<math>(a^m)^n=a^{m \cdot n}</math> | {{Caja Amarilla|texto=<center><math>a^0=1\,\!</math>{{b}}{{b}}<math>a^m \cdot a^n=a^{n+m}</math>{{b}}{{b}}<math>\cfrac{a^m}{a^n}=a^{m-n}\,\!</math>{{b}}{{b}}<math>(a^m)^n=a^{m \cdot n}</math> | ||
| </center> | </center> | ||
| Línea 210: | Línea 210: | ||
| {{p}} | {{p}} | ||
| - | ===Jerarquía de las operaciones=== | + | ===Jerarquía de las operaciones con números naturales=== |
| A la hora de operar con números naturales seguiremos las siguientes pautas: | A la hora de operar con números naturales seguiremos las siguientes pautas: | ||
| {{Caja Amarilla|texto=Se efectúan primero el contenido de los paréntesis. De las operaciones, la de mayor prioridad es la potenciación, seguida de la multiplicación y las división y, para terminar, la suma y la resta. | {{Caja Amarilla|texto=Se efectúan primero el contenido de los paréntesis. De las operaciones, la de mayor prioridad es la potenciación, seguida de la multiplicación y las división y, para terminar, la suma y la resta. | ||
Revisión de 21:09 25 jun 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Operaciones I Operaciones II Tablas de multiplicar Mi libreta | WIRIS Geogebra Calculadora Números naturales Aritmética |
Tabla de contenidos
|
Números naturales
El conjunto de los números naturales es 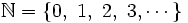 . Son infinitos y sirven para contar (números cardinales: 1, 2, 3, ...) o para ordenar (números ordinales: 1º, 2º, 3º, ...).
. Son infinitos y sirven para contar (números cardinales: 1, 2, 3, ...) o para ordenar (números ordinales: 1º, 2º, 3º, ...).
Podemos representarlos en una recta:
Operaciones con números naturales
Suma y multiplicación de números naturales
La suma (o adición) y la multiplicación (o producto) de dos números naturales es otro número natural. Por eso se dice que estas dos operaciones son leyes de composición interna.
Resta y división de números naturales
La resta (o substracción)y la división (o cociente) de dos números naturales no siempre es otro número natural. Por eso se dice que estas dos operaciones son leyes de composición externa.
Propiedades de la suma y el producto de números naturales
La suma y la multiplicación cumplen las siguientes propiedades:
- Propiedad asociativa:
- Propiedad conmutativa:
- Propiedad distributiva:
La propiedad distributiva sirve para simplificar expresiones sacando factor común. Veamos un ejemplo
Ejemplo: Sacar factor común
- Saca factor común en la expresión 16x3 − 24x2 + 4x
El factor común, que se repite en los tres sumandos, es 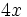 . Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común
. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común 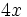 , dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
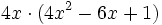
División de números naturales
La división puede verse como un reparto de un número de elementos (dividendo) en un número de partes iguales (divisor), que da como resultado el número de elementos que corresponden a cada parte (cociente) y un posible número de elementos sobrantes (resto). Si el resto es cero la división se llama exacta, si no, se llama entera.
Algoritmo de la división: En toda división, el dividendo es igual al divisor por el cociente más el resto.
|
|
donde D es el dividendo, d el divisor, c el cociente y r el resto.
Potenciación de números naturales
Una potencia de base a y exponente n consiste en multiplicar n veces la base a.
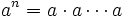
Una potencia es un modo abreviado de escribir un producto de un número por sí mismo.
En la expresión de la potencia de un número consideramos dos partes:
- La base es el número que se multiplica por sí mismo
- El exponente es el número que indica las veces que la base aparece como factor.
Una potencia se escribe tradicionalmente poniendo el número base de tamaño normal y junto a él, arriba a su derecha se pone el exponente, de tamaño más pequeño.
Para nombrar o leer una potencia decimos primeramente el número base, después decimos lo referente al exponente. Cuando el exponente es 2 se dice "elevado al cuadrado", cuando el exponente es 3 se dice "elevado al cubo". En los demás casos se dice "elevado a la cuarta, quinta, sexta... potencia".
|
Actividad Interactiva: Potencias
1. Potencia de un número.
Actividad: Observa cómo varía el resultado al modificar la base y el exponente. Haz uso de la escena anterior y contesta en tu cuaderno: a) ¿Qué valor tiene una las potencia cuya base es el número 0 sea cual sea el exponente? b) ¿Qué valor tiene una potencia cuya base es el número 1 sea cual sea el exponente? c) ¿Qué valor tienen las potencias de cualquier base cuando su exponente es el número 0 ? d) ¿Qué valor tiene una potencia cuyo exponente es el número 1 ? Cuando el exponente de una potencia es el número 1 no se pone exponente, basta con poner el número de la base |
Propiedades de las potencias de números naturales
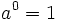
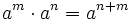
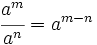
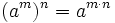
|
Actividad Interactiva: Propiedades de las potencias
1. Propiedades de las potencias de números naturales.
Actividad: En las siguientes escenas, para ver paso a paso las transformaciones debes pulsar sobre el triángulo azul de arriba de la escena.
El producto de varias potencias de la misma base equivale a otra potencia cuya base es la misma y cuyo exponente es la suma de los exponentes.
El cociente de dos potencias de la misma base equivale a otra potencia cuya base es la misma y cuyo exponente es la resta de los exponentes.
Sigue actuando sobre la escena anterior, haz que los dos exponentes sean iguales, ello dará como resultado una potencia de exponente 0. Observa el valor de esa potencia. Habrás descubierto que: Una potencia de exponente 0 vale 1.
La potencia de una potencia equivale a una potencia simple cuya base es la misma y cuyo exponente es el producto de los exponentes.
La potencia de un producto equivale al producto de potencias cuyas bases son cada uno de los factores y cuyo exponente es el mismo.
2. Autoevaluación.
Actividad: En las siguientes escenas rellena todas las cajas inferiores y pulsa "intro" al final. Cuando hayas marcado correctamente los tres aparecerá el mensaje CORRECTO, pero si marcas antes un número equivocado ya no aparecerá ese mensaje, por eso, no emplees los triángulos arriba y abajo para variar el número.
3. Juegos.
Actividad: |
Jerarquía de las operaciones con números naturales
A la hora de operar con números naturales seguiremos las siguientes pautas:
Se efectúan primero el contenido de los paréntesis. De las operaciones, la de mayor prioridad es la potenciación, seguida de la multiplicación y las división y, para terminar, la suma y la resta. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
|
Actividad Interactiva: Jerarquía de las operaciones
1. Operaciones combinadas.
Actividad: En esta actividad debes escribir en la ventana bajo la escena el número que sigue al resolver la expresión y pulsar "intro". Cuando el número marcado sea el correcto aparecerá en la escena, si no es el correcto no aparecerá. Debes hacerlo sucesivamente, paso a paso, para ello debes borrar el número anterior. No se trata de que halles directamente el resultado final. Al picar sobre inicio aparecerá otra expresión diferente de operaciones combinadas. Resuelve varias de ellas. |
Ejercicios y problemas
Ejercicios
|
Ejercicios 1. Calcula:
Solución: a) 20 b) 48 c) 16 d) 30 2. Simplifica:
Solución: a) 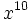 b) b) 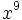 c) c) 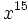 3. Simplifica:
Solución: a) 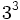 b) b) 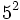 c) c) 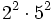 4. Extrae factor común:
Solución: a) 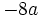 b) b) 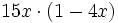 c) c) 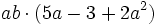 |
Problemas
|
Problemas
1. Al dividir 453 entre 32 se obtiene 5 de resto. ¿Cúal es el divisor?
Solución: El divisor es 14 (Aplicando la regla de la división)
2. Una empresa compra una máquina de café por 6.000 €. Cada mes se gasta 100 € en mantenimiento pero obtiene 350 € por la venta de café. Al cabo de 2 años y medio la vende por 4920 €. ¿Qué beneficio mensual le ha aportado la máquina?
Solución: 214 € |
Calculadora
WIRIS: Operaciones con números naturales
Revisa estos ejemplos y utiliza el editor para calcular:
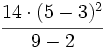
Comprueba el resultado también con tu calculadora. (Solución: 8)

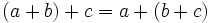
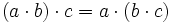
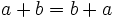
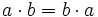
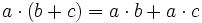
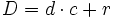
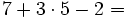
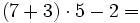
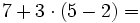
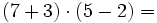
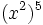 b)
b) 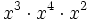 c)
c) 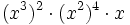
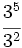 b)
b)  c)
c) 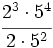
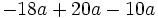 b)
b) 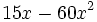 c)
c) 
