Tablas de datos

De Wikipedia

(Diferencia entre revisiones)

Revisión de 16:41 12 jun 2017

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio	Estadística (SM)		WIRIS Geogebra Calculadora

Tablas estadísticas

Son utilizadas para organizar los datos. Según el número de observaciones y según el recorrido de la variable estadística (mayor valor menos el menor valor), tenemos los siguientes tipos de tablas estadísticas:

Tablas Tipo I: Cuando el tamaño de la muestra y el recorrido de la variable son pequeños (por ejemplo, si tenemos una muestra de las edades de 5 personas), por lo que no hay que hacer nada especial simplemente anotarlas de manera ordenada en filas o columnas.

Ejemplo

Variable: "Edad de los 5 miembros de una familia"
Valores observados: 5, 8, 16, 38, 45

Tablas Tipo II: Cuando el tamaño de la muestra es grande y el recorrido de la variable es pequeño, por lo que hay valores de la variable que se repiten.

Ejemplo

Si preguntamos el número de personas activas que hay en 50 familias obtenemos la siguiente tabla:

2	1	2	2	1	2	4	2	1	1
2	3	2	1	1	1	3	4	2	2
2	2	1	2	1	1	1	3	2	2
3	2	3	1	2	4	2	1	4	1
1	3	4	3	2	2	2	1	3	3

Podemos observar que la variable toma valores comprendidos entre 1 y 4, por lo que precisaremos una tabla en la que resumamos estos datos quedando la siguiente tabla:

Personas activas	Nº de familias
1	16
2	20
3	9
4	5
Total	50

Tablas Tipo III: Se utilizan cuando el tamaño de la muestra y el recorrido de la variable son grandes, por lo que será necesario agrupar en intervalos los valores de la variable. Tambien obligatorio usarla cuando la variable sea cuantitativa continua.

Ejemplo

Si a un grupo de 30 alumnos les preguntamos el dinero que en ese momento tienen ahorrado, nos encontramos con los siguientes datos:

450	1152	250	300	175	80	25	2680	605	785
1595	2300	5000	1200	100	5	180	200	675	500
375	1500	205	985	185	125	315	425	560	1100

La variable estadística tiene un recorrido muy grande, (Mayor valor - Menor valor = 5000 - 5 = 4995), por lo que sí queremos hacer una tabla con estos datos tendremos que tomar intervalos. Para decidir la amplitud de los intervalos, necesitaremos decidir ¿cuántos intervalos queremos?. Normalmente se suele trabajar con no más de 10 o 12 intervalos.

$Amplitud\ de\ cada\ intervalo=\cfrac {Recorrido} {Num.\ de\ intervalos}$

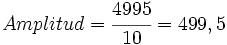
$Amplitud =\cfrac{4995}{10} = 499,5$

Por lo que tomaremos intervalos de amplitud 500

Debemos tener en cuenta las siguientes consideraciones:

Tomar pocos intervalos implica que la "pérdida de información" sea mayor.

Los intervalos serán siempre Cerrados por la izquierda y Abiertos por la Derecha [Li-1 , Li).

Con estas recomendaciones tendremos la siguiente tabla:

Intervalo	Nº de alumnos
[0,500)	16
[500,1000)	6
[1000,1500)	3
[1500,2000)	2
[2000,2500)	1
[2500,3000)	1
[3000,3500)	0
[3500,4000)	0
[4000,4500)	0
[4500,5000)	0
[5000,5500)	1

Tablas de frecuencias

Ahora iremos añadiendo más columnas según los cálculos y la información que necesitemos. Podemos ir completando la tabla con las frecuencias, que definimos a continuación:

Frecuencia absoluta. Es el número de veces que aparece cualquier valor de la variable. Se representa por 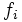$f_i\;$ (algunos autores la representan por $n_i\;$ ).
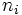Frecuencia absoluta acumulada. Es la suma de la frecuencia absoluta de un valor de la variable con todos los anteriores. Se representa por 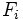$F_i\;$ (algunos autores la representan por $N_i\;$ ).
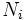Frecuencia relativa. Es el cociente entre la frecuencia absoluta y el número de datos, 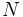$N\;$ . Se representa por 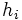$h_i\;$ (algunos autores la representan por 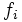$f_i\;$ ). Al multiplicarla por 100 obtenemos el porcentaje de individuos que presentan esta característica.
Frecuencia relativa acumulada. Es la suma de la frecuencia relativa de un valor de la variable con todos los anteriores. También se puede definir como el cociente entre la frecuencia absoluta acumulada y el número total de datos. Se representa por 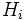$H_i\;$ (algunos autores la representan por $F_i\;$ ).

Tablas de frecuencias

Tutorial (Tipo II) (6'59") Sinopsis:

Tabla de distribución de frecuencias para muchos datos discretos con recorrido pequeño (Tipo II). Ejemplo.

Tutorial (Tipo III) (7'45") Sinopsis:

Tabla de distribución de frecuencias con intervalos (Tipo III). Ejemplo.

Ejemplo 1 (17'24") Sinopsis:

Tabla de distribución de frecuencias para muchos datos discretos con recorrido pequeño (Tipo II).

Ejemplo 2 (12'01") Sinopsis:

Tabla de distribución de frecuencias para muchos datos discretos con recorrido pequeño (Tipo II).

Ejemplo 3 (27'01") Sinopsis:

Tabla de distribución de frecuencias con intervalos (Tipo III).

Ejemplo 4 (15'47") Sinopsis:

Tabla de distribución de frecuencias con intervalos (Tipo III).

Ejemplo 5 (20'14") Sinopsis:

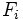Tabla de distribución de frecuencias con intervalos (Tipo III).

Actividades

Tablas de frecuencias: Variable cuantitativa discreta. Descripción:

Se recuenta el número de hermanos de 11 personas y se obtiene los siguientes resultados:

2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2

Construye en tu cuaderno la tabla de frecuencias.
Una vez que la tienes en tu cuaderno, constrúyela con la escena y compara los resultados.

Tablas de frecuencias: Variable cuantitativa continua. Descripción:

Se pregunta por la estatura a 11 personas y se obtiene los siguientes resultados:

1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66

Construye en tu cuaderno la tabla de frecuencias.
Una vez que la tienes en tu cuaderno, constrúyela con la escena y compara los resultados.

Como habrás podido observar, en las actividades anteriores sólo se han visto variables cuantitativas. Esto se debe a que si la variable no es númérica únicamente tendría sentido construir en la tabla las columnas de frecuencias absolutas y relativas, pero no las acumuladas.

Ejercicios propuestos

A partir de las dos actividades anteriores contesta a los siguientes ejercicios:

Ejercicio 1:

a) ¿Qué significado tiene cada uno de los valores de la frecuencia absoluta acumulada?

b) ¿Tiene sentido esta columna si no están ordenados los valores de la variable?

Ejercicio 2:

a) Modifica los valores de la variable pero no los de las frecuencias. ¿Influye en el resto de la tabla?

b) Modifica ahora los valores de las frecuencias y observa como varía las demás columnas (puedes incluir más valores de la variable). ¿Cuál es la última frecuencia absoluta acumulada? ¿Por qué?

c) ¿Cuál es la última frecuencia relativa acumulada? ¿Por qué?

d) ¿Cómo se puede obtener el porcentaje de individuos que presentan cada uno de los valores de la variable?

Obtenido de "http://maralboran.org/wikipedia/index.php/Tablas_de_datos"

Categorías: Matemáticas | Estadística

 Como habrás podido observar, en las actividades anteriores sólo se han visto variables cuantitativas. Esto se debe a que si la variable no es númérica únicamente tendría sentido construir en la tabla las columnas de frecuencias absolutas y relativas, pero no las acumuladas.
 {{p}}
-A partir de las dos actividades anteriores contesta a los siguientes ejercicios:
 {{ejercicio
 |titulo=Ejercicios propuestos
-|cuerpo=
+|cuerpo=A partir de las dos actividades anteriores contesta a los siguientes ejercicios:
 '''Ejercicio 1:'''
 :a) ¿Qué significado tiene cada uno de los valores de la frecuencia absoluta acumulada?

Tablas de datos

De Wikipedia

Revisión de 16:41 12 jun 2017

Tablas estadísticas

Tablas de frecuencias

Actividades

Vistas

Herramientas personales

Menú

Buscar

Herramientas