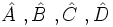Cuadriláteros (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:21 20 jul 2017 Coordinador (Discusión | contribuciones) (→Diagonales y ejes de simetría de los paralelogramos) ← Ir a diferencia anterior |
Revisión de 08:31 20 jul 2017 Coordinador (Discusión | contribuciones) (→Diagonales de los paralelogramos) Ir a siguiente diferencia → |
||
| Línea 77: | Línea 77: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ==Construcciones== | ||
| + | {{Video_enlace_pdd | ||
| + | |titulo1=Construcción de un cuadrado conocido el lado | ||
| + | |duracion=1´21" | ||
| + | |url1=https://www.youtube.com/watch?v=f5k8toYa5wU&index=3&list=PLoahkz-APounI180m5GOkSceyCqqT0vB_ | ||
| + | |sinopsis=Construcción de un cuadrado conocido el lado, con regla y compás. | ||
| + | }} | ||
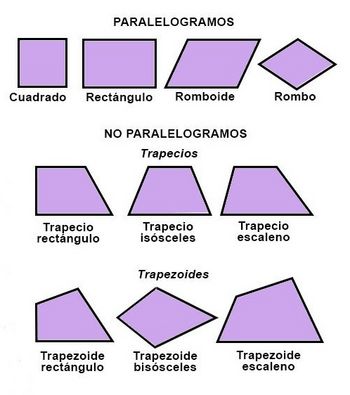
| ==Ejes de simetría de los paralelogramos== | ==Ejes de simetría de los paralelogramos== | ||
Revisión de 08:31 20 jul 2017
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Cuadrilátero
|
Propiedades Todo cuadrilátero cumple las siguientes propiedades:
Nomenclatura:
|
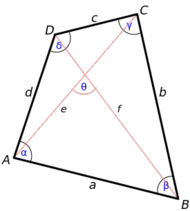
Clasificación de los cuadriláteros
Los cuadriláteros se clasifican, atendiendo al paralelismo de sus lados, en:
Los paralelogramos se clasifican, atendiendo a sus lados y a sus ángulos, en:
Los trapecios se clasifican en:
|
Actividades en las que podrás aprender el concepto de cuadrilátero, identificar sus elementos y clasificar los cuadriláteros atendiendo al número de lados paralelos que poseen.
Actividades en las que podrás aprender los distintos tipos de paralelogramos.
Diagonales de los paralelogramos
Construcciones
Construcción de un cuadrado conocido el lado, con regla y compás.