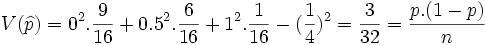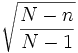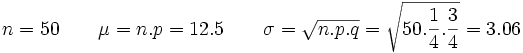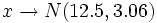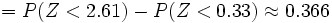Distribuciones muestrales. Teorema central del límite
De Wikipedia
| Revisión de 11:07 7 jul 2007 Juanmf (Discusión | contribuciones) (→Teorema central del límite) ← Ir a diferencia anterior |
Revisión de 11:08 7 jul 2007 Juanmf (Discusión | contribuciones) (→Teorema central del límite) Ir a siguiente diferencia → |
||
| Línea 149: | Línea 149: | ||
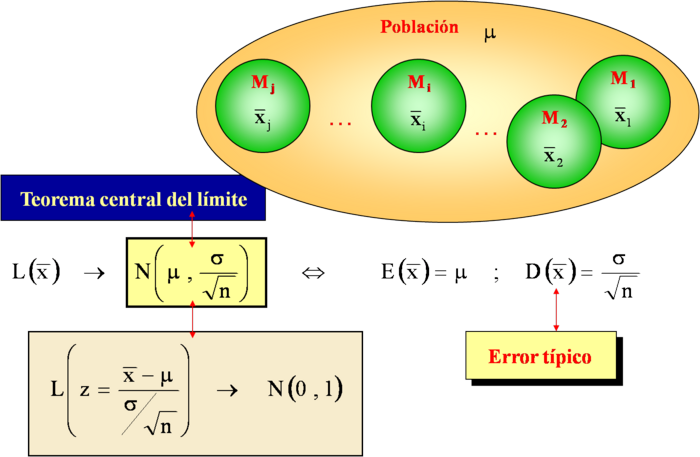
| ==Teorema central del límite== | ==Teorema central del límite== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | La distribución de medias muestrales tiende hacia una distribución normal, aunque las muestras procedan de una distribución no normal. | + | '''La distribución de medias muestrales tiende hacia una distribución normal, aunque las muestras procedan de una distribución no normal.''' |
| <center> | <center> | ||
Revisión de 11:08 7 jul 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio Indice Estadistica | Inferencia | WIRIS Geogebra Calculadora |
Distribución muestral de las proporciones
Vamos a obtener experimentalmente la distribución de las proporciones muestrales. Para ello consideremos el conjunto de figuras:
La proporción poblacional de triángulos es 1/4.
Consideremos todas las muestras de tamaño 2 posibles, mediante muestreo aleatorio simple (con reemplazamiento). Hallamos la distribución de probabilidad de la proporción muestral (nombrada por 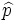 ):
):

Calculamos su esperanza matemática y la varianza:
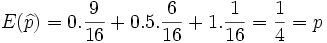
|
El número de éxitos x de una muestra de tamaño n, se distribuye de forma binomial B(n, p); si la aproximamos a una normal será 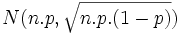 . Como
. Como 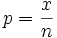 , dividiendo x por n se tiene que:
, dividiendo x por n se tiene que:
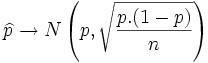 |
Si la población es finita y la extracción simultánea o sin reposición, la desviación típica va multiplicada por la siguiente expresión:
|
|
Ejemplo:Validación experimental (proporción)
De la población que consta de 4 circulos de color blanco, azul, rojo y verde, extrae todas las muestra posible de tamaño 2 de dos formas distintas:
a) Simultánea (sin reposición y sin que importe el orden)
b) Sucesiva sin reposición (importa el orden).
Calcula la distribución de probabilidad de la proporción muestral y con ella la esperanza y la varianza. Comprueba el resultado anterior.
|
Actividad 1 |
|
Ejercicios: Distribución proporción muestral 1. En una localidad de 6000 habitantes, la proporción de menores de 16 años es p=1/4. a) ¿Cuál es la distribución de la proporción de menores de 16 años en muestras de 50 habitantes de dicha población?. b) Halla la probabilidad de que, en una muestra de 50 habitantes, haya entre 14 y 20 habitantes menores de 16 años?.Solución: a) 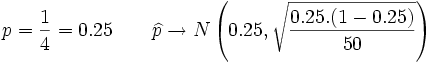
b)Siendo se tiene que: 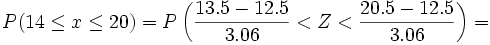
|
Distribución muestral de las medias
Vamos a obtener experimentalmente la distribución de las medias muestrales. Para ello consideremos la siguiente población:

Consideremos todas las muestras de tamaño 2 posibles, mediante muestreo aleatorio simple (con reemplazamiento). Hallamos la distribución de probabilidad de la media muestral
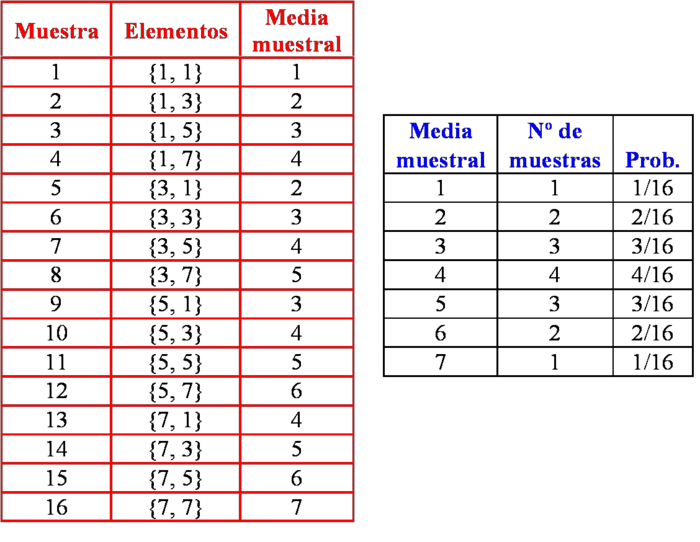
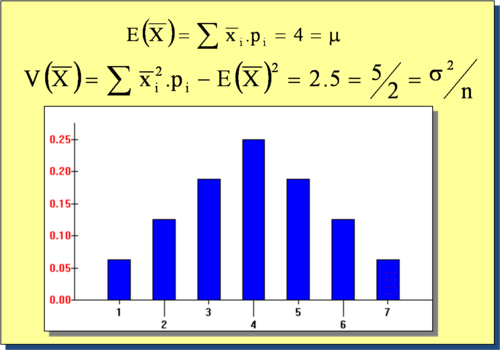
Como se puede observar:
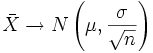
|
Si la población es finita y la extracción simultánea o sin reposición, la desviación típica va multiplicada por la siguiente expresión:
|
|
|
Actividad 1 |