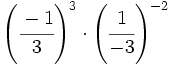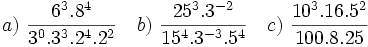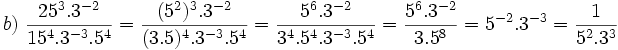Potencias
De Wikipedia
| Revisión de 16:05 17 oct 2007 Coordinador (Discusión | contribuciones) (→Ejercicios) ← Ir a diferencia anterior |
Revisión de 16:05 17 oct 2007 Coordinador (Discusión | contribuciones) (→Ejercicios) Ir a siguiente diferencia → |
||
| Línea 289: | Línea 289: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas:''Propiedades de las potencias'' | + | {{AI2|titulo=Actividades Interactivas: ''Propiedades de las potencias'' |
| |cuerpo= | |cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
Revisión de 16:05 17 oct 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Potencias | WIRIS Geogebra Calculadora Números naturales Aritmética |
Tabla de contenidos |
Potencias de naturales
Una potencia de base  y exponente
y exponente  consiste en multiplicar
consiste en multiplicar  veces la base
veces la base  .
.
Una potencia es un modo abreviado de escribir un producto de un número por sí mismo.
En la expresión de la potencia de un número consideramos dos partes:
- La base es el número que se multiplica por sí mismo
- El exponente es el número que indica las veces que la base aparece como factor.
Una potencia se escribe tradicionalmente poniendo el número base de tamaño normal y junto a él, arriba a su derecha se pone el exponente, de tamaño más pequeño.
Para nombrar o leer una potencia decimos primeramente el número base, después decimos lo referente al exponente. Cuando el exponente es 2 se dice "elevado al cuadrado", cuando el exponente es 3 se dice "elevado al cubo". En los demás casos se dice "elevado a la cuarta, quinta, sexta... potencia".
|
Actividad Interactiva: Potencias
Actividad 1. Potencia de un número natural.
Actividad: Observa cómo varía el resultado al modificar la base y el exponente. Haz uso de la escena anterior y contesta en tu cuaderno:
|
Propiedades de las potencias de naturales
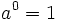
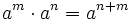
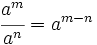
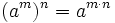
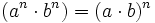
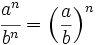
|
Actividad Interactiva: Propiedades de las potencias
Actividad 1. Propiedades de las potencias de números naturales.
Actividad: En las siguientes escenas, para ver paso a paso las transformaciones debes pulsar sobre el triángulo azul de arriba de la escena.
El producto de varias potencias de la misma base equivale a otra potencia cuya base es la misma y cuyo exponente es la suma de los exponentes.
El cociente de dos potencias de la misma base equivale a otra potencia cuya base es la misma y cuyo exponente es la resta de los exponentes.
Sigue actuando sobre la escena anterior, haz que los dos exponentes sean iguales, ello dará como resultado una potencia de exponente 0. Observa el valor de esa potencia. Habrás descubierto que: Una potencia de exponente 0 vale 1.
La potencia de una potencia equivale a una potencia simple cuya base es la misma y cuyo exponente es el producto de los exponentes.
La potencia de un producto equivale al producto de potencias cuyas bases son cada uno de los factores y cuyo exponente es el mismo.
Actividad 2. Autoevaluación.
Actividad: En las siguientes escenas rellena todas las cajas inferiores y pulsa "intro" al final. Cuando hayas marcado correctamente los tres aparecerá el mensaje CORRECTO, pero si marcas antes un número equivocado ya no aparecerá ese mensaje, por eso, no emplees los triángulos arriba y abajo para variar el número.
Actividad 3. Juegos.
|
Potencias de enteros
Las potencias de enteros cumplen las mismas propiedades que las potencias de números naturales.
Potencia de base negativa:
Al elevar un número negativo a una potencia, el resultado es positivo si el exponente es par y negativo si es impar.
|
Actividad Interactiva: Potencias de números enteros
Actividad 1. Potencias de base negativa.
Actividad: Calcula las siguientes potencias y comprueba los resultados en la escena siguiente: a) ( − 3)4 b) ( − 4)5 c) ( − 10)5 d) ( − 2)10 Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. |
Potencias de fracciones
Las potencias con números racionales cumplen las mismas propiedades que con números naturales y enteros.Pulsa los botones para obtener ejemplos de cada tipo:
Tan sólo queda añadir el siguiente caso:
Potencias de exponente negativo
Sea 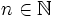 , se define la potencia de exponente negativo como:
, se define la potencia de exponente negativo como:
|
|
Como consecuencia, 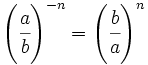 .
.
|
Actividad Interactiva: Potencias de exponente negativo
Actividad 1. Potencias de exponente negativo.
Actividad: Calcula las siguientes potencias y comprueba los resultados en la escena siguiente: a) 3 − 5 b) 5 − 3 c) 7 − 2 d) 2 − 7 Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba.
Actividad 2. Autoevaluación.
Actividad: Pulsa el botón "EJERCICIO" y lee atentamente el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien. |
Ejercicios
|
Actividad Interactiva: Operaciones con potencias
Actividad 1. Autoevaluación: Operaciones con potencias de enteros y racionales.
Actividad: Pulsa el botón EJERCICIO para ver el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena (de forma que la base no sea una potencia) y pulsas el botón SOLUCIÓN para ver si lo has hecho bien. |
|
Actividades Interactivas: Propiedades de las potencias
Actividad 1: Producto de potencias.
Actividad: Escribe en tu cuaderno los siguientes productos en forma de potencia:
Actividad 2: Cociente de potencias.
Actividad: Escribe en tu cuaderno los siguientes cocientes en forma de potencia:
Actividad 3: Potencia de un producto.
Actividad: Expresa en forma de producto de potencias los siguientes expresiones:
Actividad 4: Potencia de un cociente.
Actividad: Expresa en forma de cociente de potencias los siguientes expresiones:
Actividad 5: Potencia de una potencia.
Actividad: Escribe en tu cuaderno las siguientes potencias en forma de potencia con un solo exponente:
|
|
Ejercicios: Potencias de naturales 1. Simplifica:
Solución: a) 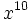 b) b) 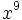 c) c) 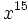 2. Simplifica:
Solución: a) 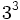 b) b) 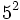 c) c) 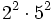 |
|
Ejercicios: Potencias de enteros 1. Calcula:
Solución: a) -8 b) -16 c) 64 d) 1 e) -1 f) -1 |
|
Ejercicios: Potencias de fracciones 1. Simplifica y expresa en forma de fracción:
Solución: a) 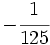 b) b) 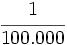 c) c) 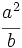 2. Simplifica:
Solución: a) 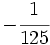 b) b) 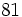 c) c) 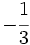 3. Calcula utilizando las propiedades de las potencias:
Solución: 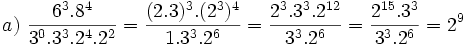
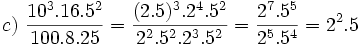 |
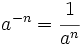
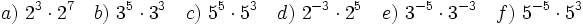
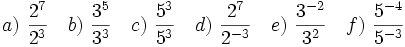
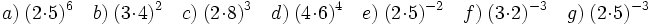
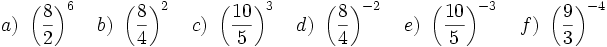
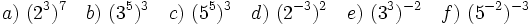
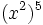 b)
b) 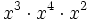 c)
c) 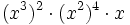
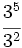 b)
b)  c)
c) 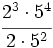
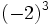 b)
b) 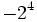 c)
c) 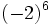 d)
d) 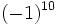 e)
e) 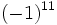 f)
f) 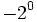
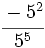 b)
b) 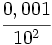 c)
c) 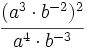
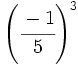 b)
b) ![\left [ \left ( \cfrac{-1}{3} \right )^{-2} \right ]^2](/wikipedia/images/math/1/4/e/14e6c8e9222f905775e21fb947d71f2c.png) c)
c)