Sucesiones
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:42 12 dic 2007 Coordinador (Discusión | contribuciones) (→Actividades) ← Ir a diferencia anterior |
Revisión de 16:04 12 dic 2007 Coordinador (Discusión | contribuciones) (→Video) Ir a siguiente diferencia → |
||
| Línea 84: | Línea 84: | ||
| ==Video== | ==Video== | ||
| {{Video | {{Video | ||
| - | |titulo=Fibonacci. La magia de los números | + | |titulo=Fibonacci: La magia de los números |
| |sinopsis=Leonardo de Pisa, más conocido como Fibonacci, es el autor de la primera summa matemática de la Edad Media, el Liber Abaci. Con este libro introduce en la Europa cristiana las nueve cifras hindúes y el signo del cero. Pero además brinda a los calculistas de la época reglas claras para realizar operaciones con estas cifras tanto con números enteros como con fracciones. Pero Fibonacci es más conocido entre los matemáticos por la curiosa sucesión de números que lleva su nombre y en la que cada término es la suma de los dos anteriores. Esta sucesión es una auténtica fuente de agradables sorpresas. Analizaremos las sugerentes relaciones que existen entre sus términos y descubriremos su presencia en fenómenos naturales coma la ramificación de algunas plantas, la distribución de los piñones en las piñas y de las pipas en los girasoles. Y, aunque en principio cueste trabajo creérselo, veremos que está directamente emparentada con un viejo amigo nuestro: el número áureo. | |sinopsis=Leonardo de Pisa, más conocido como Fibonacci, es el autor de la primera summa matemática de la Edad Media, el Liber Abaci. Con este libro introduce en la Europa cristiana las nueve cifras hindúes y el signo del cero. Pero además brinda a los calculistas de la época reglas claras para realizar operaciones con estas cifras tanto con números enteros como con fracciones. Pero Fibonacci es más conocido entre los matemáticos por la curiosa sucesión de números que lleva su nombre y en la que cada término es la suma de los dos anteriores. Esta sucesión es una auténtica fuente de agradables sorpresas. Analizaremos las sugerentes relaciones que existen entre sus términos y descubriremos su presencia en fenómenos naturales coma la ramificación de algunas plantas, la distribución de los piñones en las piñas y de las pipas en los girasoles. Y, aunque en principio cueste trabajo creérselo, veremos que está directamente emparentada con un viejo amigo nuestro: el número áureo. | ||
| |duracion=16' | |duracion=16' | ||
Revisión de 16:04 12 dic 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Definiciones
Sucesión de números: Conjunto de infinitos números ordenados. Ejemplo: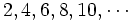 
Término de una sucesión: Cada uno de los números que la componen. Se nombran con una letra y un subíndice que depende del lugar que el término ocupa en la sucesión.
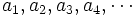
Según lo dicho, 
designará al término que ocupa el décimo lugar dentro de una sucesión, en el ejemplo es el 20.
A veces, podemos encontrar una expresión (fórmula) que sirve para obtener un término cualquiera de la sucesión con solo saber el lugar que este ocupa. A esta expresión se le llama término general. El término general de la sucesión del ejemplo es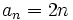 
Actividades
 Actividades Interactivas: Término general de una sucesión
Actividad 1: Autoevaluación: Hallar el término general de una sucesión.
|
 Ejercicios: Sucesiones
1. Escribe los cinco primeros términos de la sucesión cuyo primer término es 2 y todos los demás se obtienen sumando 5 al término anterior.
Solución: 2,7,12,17,22,27....
2. El término general de una sucesión es
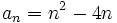 . Calcula los cinco primeros términos y Solución: -3,-4,-3,0,5; a10 = 102 − 4.10 = 60 3. Intenta escribir una expresión que sirva para calcular cualquier término de las sucesiones siguientes: a) 1,2,3,4,5,... b) 1,4,9,16,... c) 1,3,5,7,... d) 1/2,1/4,1/8,... e) -1,1,-1,1,-1,... f) 1,-1,1,-1,1,...Solución: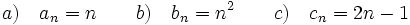 
 |
Actividad Interactiva: Sucesiones
Actividad 1: Representación gráfica de los elementos de una sucesión.
Actividad:
|
Video
Video: Fibonacci: La magia de los números (16')
Sinopsis:
Leonardo de Pisa, más conocido como Fibonacci, es el autor de la primera summa matemática de la Edad Media, el Liber Abaci. Con este libro introduce en la Europa cristiana las nueve cifras hindúes y el signo del cero. Pero además brinda a los calculistas de la época reglas claras para realizar operaciones con estas cifras tanto con números enteros como con fracciones. Pero Fibonacci es más conocido entre los matemáticos por la curiosa sucesión de números que lleva su nombre y en la que cada término es la suma de los dos anteriores. Esta sucesión es una auténtica fuente de agradables sorpresas. Analizaremos las sugerentes relaciones que existen entre sus términos y descubriremos su presencia en fenómenos naturales coma la ramificación de algunas plantas, la distribución de los piñones en las piñas y de las pipas en los girasoles. Y, aunque en principio cueste trabajo creérselo, veremos que está directamente emparentada con un viejo amigo nuestro: el número áureo.
