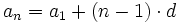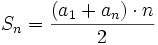Progresiones aritméticas
De Wikipedia
| Revisión de 18:38 17 dic 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:19 8 ene 2008 Coordinador (Discusión | contribuciones) (→Suma de términos de una progresión aritmética) Ir a siguiente diferencia → |
||
| Línea 61: | Línea 61: | ||
| |enunciado= | |enunciado= | ||
| La suma de los '''n''' primeros términos de una progresión aritmética es: | La suma de los '''n''' primeros términos de una progresión aritmética es: | ||
| - | {{Caja|contenido=<math>S_n=\frac{(a_1+a_n).n}{2}</math>}} | + | {{Caja|contenido=<math>S_n=\frac{(a_1+a_n) \cdot n}{2}</math>}} |
| {{p}} | {{p}} | ||
| |demo= | |demo= | ||
Revisión de 11:19 8 ene 2008
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Definición
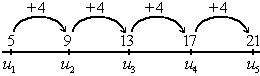
Una progresión aritmética es una sucesión de números en la que cada término se obtiene sumando al anterior una cantidad fija,  , que llamaremos diferencia.
, que llamaremos diferencia.
Por ejemplo:
es una progresión aritmética con diferencia d=4.
Término general de una progresión aritmética
Término general de una progresión aritmética
Sean 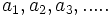 términos de una progresión aritmética de diferencia
términos de una progresión aritmética de diferencia  .
.
|
|
En efecto, razonando por inducción:
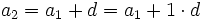
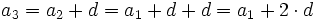
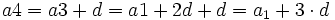
........................
|
|
|
Actividad Interactiva: Progresiones aritméticas
Actividad 1: Ejercicios de autoevaluación sobre progresiones aritméticas.
Actividad:
|
Suma de términos de una progresión aritmética
Suma de términos de una progresión aritmética
La suma de los n primeros términos de una progresión aritmética es:
|
|
El porqué de esta fórmula se deduce de la siguiente historia:
En un pequeño pueblo de Alemania (Brunswick), un profesor castigaba a sus alumnos haciéndoles sumar números consecutivos (por ejemplo sumar los 100 primeros números naturales). Era un duro castigo, pues había que hacer muchas sumas (1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, 10 + 5 = 15,...) y era fácil equivocarse.
Pero... una vez, uno de los niños le dio la solución en un tiempo sorprendente, el profesor le preguntó ¿cómo lo has hecho? El niño le dijo: 1 + 100= 101, 2 + 99 = 101, 3 + 98 = 101,... siempre suma 101 y hay 50 sumas, en total 50 * 101 = 5050. El profesor quedó tan impresionado que le regaló un libro de Aritmética.
Ese niño tenía 10 años y se llamaba Carl Friedrich Gaüss. Fue uno de los mas grandes matemáticos.
Intenta enterarte de algo más sobre él.
Gauss y el ajedrezEjercicios
|
Problemas 1. Comprueba que las sucesiones siguientes son progresiones aritméticas. Calcula la diferencia y el término general de cada una de ellas. a) 1, -1, -3, -5, -7,.... b) 2, 5, 8, 11, 14,.... c) -7, -5, -3, -1, 1,...Solución: 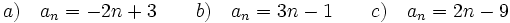
2. Si
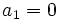 y y 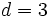 , en una progresión aritmética, ¿cuánto vale , en una progresión aritmética, ¿cuánto vale 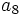 ? ?Solución: 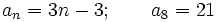
3. Si
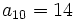 y y 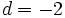 , calcular , calcular 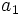 . .Solución: 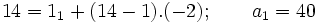
4. Al excavar tierra para hacer un túnel se pagan 700€ por el primer metro y 95€ de aumento por cada metro sucesivo. ¿Cuánto se pagará por el décimo metro excavado? Calcular el total abonado por los 10 metros excavados.
Solución: 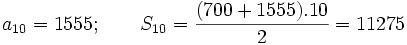 |