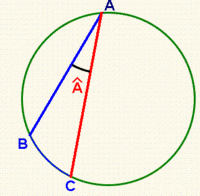
Ángulos en la circunferencia
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 22:45 18 dic 2007 Coordinador (Discusión | contribuciones) (→Ángulo inscrito) ← Ir a diferencia anterior |
Revisión de 22:45 18 dic 2007 Coordinador (Discusión | contribuciones) (→Ángulo inscrito) Ir a siguiente diferencia → |
||
| Línea 30: | Línea 30: | ||
| |titulo=Propiedades: ''Ángulo inscrito'' | |titulo=Propiedades: ''Ángulo inscrito'' | ||
| |enunciado= | |enunciado= | ||
| - | :a) La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente. | + | a) La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente. |
| - | :b) Como consecuencia, dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales. | + | b) Como consecuencia, dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales. |
| - | :c) Como caso particular, todo ángulo inscrito en una semicircunferncia es recto. | + | c) Como caso particular, todo ángulo inscrito en una semicircunferncia es recto. |
| |demo= | |demo= | ||
| - | :a) Mueve los puntos A y B y comprueba que el ángulo inscrito mide la mitad que el arco central que le corresponde. | + | a) Mueve los puntos A y B y comprueba que el ángulo inscrito mide la mitad que el arco central que le corresponde. |
| - | :b) Mueve el vértice V y observa que no varía la medida del ángulo <math>\widehat{AVB}</math>. | + | b) Mueve el vértice V y observa que no varía la medida del ángulo <math>\widehat{AVB}</math>. |
| <center><iframe> | <center><iframe> | ||
Revisión de 22:45 18 dic 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Ángulos (1ºESO) | WIRIS Geogebra Calculadora |
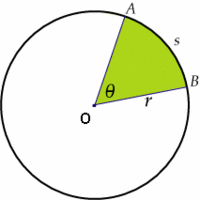
Ángulo central
Ángulo inscrito
Propiedades: Ángulo inscrito
a) La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente. b) Como consecuencia, dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales. c) Como caso particular, todo ángulo inscrito en una semicircunferncia es recto.
Demostración:
a) Mueve los puntos A y B y comprueba que el ángulo inscrito mide la mitad que el arco central que le corresponde.
b) Mueve el vértice V y observa que no varía la medida del ángulo 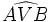 .
.
c) Sea AB un diámetro de la circunferencia: 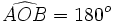 . Por el apartado a), el ángulo inscrito
. Por el apartado a), el ángulo inscrito 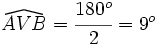 .
.
 y su arco correspondiente AB.
y su arco correspondiente AB.
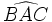 .
.