Ángulos en la circunferencia
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 23:16 18 dic 2007 Coordinador (Discusión | contribuciones) (→Propiedades) ← Ir a diferencia anterior |
Revisión de 23:19 18 dic 2007 Coordinador (Discusión | contribuciones) (→Propiedades) Ir a siguiente diferencia → |
||
| Línea 30: | Línea 30: | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| |texto= | |texto= | ||
| - | '''a)''' La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente. | + | '''a)''' Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales. |
| {{Desplegable | {{Desplegable | ||
| |titulo=Demostración: | |titulo=Demostración: | ||
| - | |contenido=Mueve los puntos A y B y comprueba que el ángulo inscrito mide la mitad que el arco central que le corresponde. | + | |contenido=Mueve el vértice V y observa que no varía la medida del ángulo <math>\widehat{AVB}</math>. |
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geometria/geoweb/circun4_3.html | + | url=http://maralboran.org/web_ma/geometria/geoweb/circun4_2.html |
| width=380 | width=380 | ||
| height=350 | height=350 | ||
| Línea 42: | Línea 42: | ||
| </iframe></center> | </iframe></center> | ||
| }} | }} | ||
| - | '''b)''' Como consecuencia, dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales. | + | |
| + | '''b)''' La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente. | ||
| {{Desplegable | {{Desplegable | ||
| |titulo=Demostración: | |titulo=Demostración: | ||
| - | |contenido=Mueve el vértice V y observa que no varía la medida del ángulo <math>\widehat{AVB}</math>. | + | |contenido=Mueve los puntos A y B y comprueba que el ángulo inscrito mide la mitad que el arco central que le corresponde. |
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geometria/geoweb/circun4_2.html | + | url=http://maralboran.org/web_ma/geometria/geoweb/circun4_3.html |
| width=380 | width=380 | ||
| height=350 | height=350 | ||
| Línea 54: | Línea 55: | ||
| </iframe></center> | </iframe></center> | ||
| }} | }} | ||
| - | '''c)''' Como caso particular, todo ángulo inscrito en una semicircunferncia es recto. | + | '''c)''' Todo ángulo inscrito en una semicircunferncia es recto. |
| {{Desplegable | {{Desplegable | ||
| |titulo=Demostración: | |titulo=Demostración: | ||
Revisión de 23:19 18 dic 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Ángulos (1ºESO) | WIRIS Geogebra Calculadora |
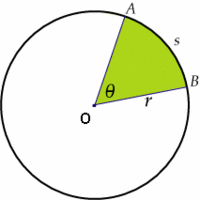
Ángulo central
Ángulo inscrito
Propiedades
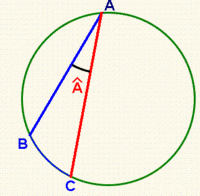
a) Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales.
Demostración:
Mueve el vértice V y observa que no varía la medida del ángulo 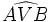 .
.
b) La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente.
Demostración:
Mueve los puntos A y B y comprueba que el ángulo inscrito mide la mitad que el arco central que le corresponde.
c) Todo ángulo inscrito en una semicircunferncia es recto.
Demostración:
Sea AB un diámetro de la circunferencia: 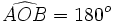 . Por el apartado a), el ángulo inscrito
. Por el apartado a), el ángulo inscrito 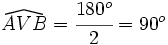 .
.
 y su arco correspondiente AB.
y su arco correspondiente AB.
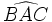 .
.