Funciones lineales: Función afín
De Wikipedia
| Revisión de 11:36 6 dic 2008 Coordinador (Discusión | contribuciones) (→Función lineal afín) ← Ir a diferencia anterior |
Revisión de 11:52 6 dic 2008 Coordinador (Discusión | contribuciones) (→Función lineal afín) Ir a siguiente diferencia → |
||
| Línea 16: | Línea 16: | ||
| |enunciado= | |enunciado= | ||
| {{p}} | {{p}} | ||
| + | |||
| #Un estanque tiene un grifo que vierte 5 litros por minuto. Haz una tabla que relacione el tiempo transcurrido (en minutos) y el volumen (en litros) de estanque que se llena. Escribe la fórmula que relaciona el volumen y el tiempo. Representa gráficamente los resultados. | #Un estanque tiene un grifo que vierte 5 litros por minuto. Haz una tabla que relacione el tiempo transcurrido (en minutos) y el volumen (en litros) de estanque que se llena. Escribe la fórmula que relaciona el volumen y el tiempo. Representa gráficamente los resultados. | ||
| #Repite el apartado anterior suponiendo que el estanque tiene un volumen inicial de 20 litros. | #Repite el apartado anterior suponiendo que el estanque tiene un volumen inicial de 20 litros. | ||
| #¿Y si partiésemos de un volumen inicial de 10 litros, cuáles serían los resultados? | #¿Y si partiésemos de un volumen inicial de 10 litros, cuáles serían los resultados? | ||
| #Compara las gráficas obtenidas e indica que tienen en común y en qué se diferencian. | #Compara las gráficas obtenidas e indica que tienen en común y en qué se diferencian. | ||
| + | #¿Qué fórmula correspondería a esta situación gráfica? | ||
| + | <center>[[Imagen:afin4.jpg|300px]]</center> | ||
| |sol= | |sol= | ||
| + | {{tabla75 | ||
| + | |celda1= | ||
| 1. Un estanque tiene un grifo que vierte 5 litros por minuto. | 1. Un estanque tiene un grifo que vierte 5 litros por minuto. | ||
| - | Partimos de que el estanque se encuentra vacío inicialmente. Completa la tabla: | + | Partimos de que el estanque se encuentra vacío inicialmente. |
| - | + | Completa la tabla: | |
| + | {{p}} | ||
| <table border="1" width="100%"> | <table border="1" width="100%"> | ||
| <tr> | <tr> | ||
| Línea 44: | Línea 50: | ||
| </tr> | </tr> | ||
| </table> | </table> | ||
| - | + | {{p}} | |
| La fórmula que expresa la relación entre el volumen y el tiempo es: | La fórmula que expresa la relación entre el volumen y el tiempo es: | ||
| {{Caja|contenido=<math>V=5 \cdot t</math>}} | {{Caja|contenido=<math>V=5 \cdot t</math>}} | ||
| + | |celda2= | ||
| + | [[Imagen:afin1.jpg|300px]] | ||
| + | }} | ||
| + | {{tabla75 | ||
| + | |celda1= | ||
| + | 2. Supongamos ahora que el estanque tiene inicialmente un volumen de 20 litros. | ||
| + | Completa la tabla: | ||
| + | {{p}} | ||
| + | <table border="1" width="100%"> | ||
| + | <tr> | ||
| + | <td width="13%"><p align="center"><strong><font size="-2">Tiempo (min)</font></strong></p> | ||
| + | </td> | ||
| + | <td align="center" width="9%"><strong>0</strong></td> | ||
| + | <td align="center" width="11%"><strong>1</strong></td> | ||
| + | <td align="center" width="11%"><strong>4</strong></td> | ||
| + | <td align="center" width="11%"><strong>6</strong></td> | ||
| + | <td align="center" width="11%"><strong>t</strong></td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td width="13%"><p align="center"><strong><font size="-2">Volumen (litros)</font></strong></p> | ||
| + | </td> | ||
| + | <td align="center" width="9%"><strong>20</strong></td> | ||
| + | <td align="center" width="11%"><strong>25</strong></td> | ||
| + | <td align="center" width="11%"><strong>{{b}}</strong></td> | ||
| + | <td align="center" width="11%"><strong>{{b}}</strong></td> | ||
| + | <td align="center" width="11%"><strong>{{b}}</strong></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | {{p}} | ||
| + | La fórmula que expresa la relación entre el volumen y el tiempo ahora es: | ||
| + | |||
| + | {{Caja|contenido=<math>V=5 \cdot t+20</math>}} | ||
| + | |celda2= | ||
| + | [[Imagen:afin2.jpg|300px]] | ||
| + | }} | ||
| + | {{tabla75 | ||
| + | |celda1= | ||
| + | 3. Ahora supondremos que el estanque tiene inicialmente un volumen de 10 litros. | ||
| + | Completa la tabla: | ||
| + | {{p}} | ||
| + | <table border="1" width="100%"> | ||
| + | <tr> | ||
| + | <td width="13%"><p align="center"><strong><font size="-2">Tiempo (min)</font></strong></p> | ||
| + | </td> | ||
| + | <td align="center" width="9%"><strong>0</strong></td> | ||
| + | <td align="center" width="11%"><strong>1</strong></td> | ||
| + | <td align="center" width="11%"><strong>4</strong></td> | ||
| + | <td align="center" width="11%"><strong>6</strong></td> | ||
| + | <td align="center" width="11%"><strong>t</strong></td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td width="13%"><p align="center"><strong><font size="-2">Volumen (litros)</font></strong></p> | ||
| + | </td> | ||
| + | <td align="center" width="9%"><strong>10</strong></td> | ||
| + | <td align="center" width="11%"><strong>15</strong></td> | ||
| + | <td align="center" width="11%"><strong>{{b}}</strong></td> | ||
| + | <td align="center" width="11%"><strong>{{b}}</strong></td> | ||
| + | <td align="center" width="11%"><strong>{{b}}</strong></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | {{p}} | ||
| + | La fórmula que expresa la relación entre el volumen y el tiempo ahora es: | ||
| + | |||
| + | {{Caja|contenido=<math>V=5 \cdot t+10</math>}} | ||
| + | |celda2= | ||
| + | [[Imagen:afin3.jpg|300px]] | ||
| + | }} | ||
| + | 4. Las graficas son rectas paralelas que cortan al eje de ordenadas a una altura que coincide con el volumen inicial del estanque. Por tanto, tienen en común que tienen la misma inclinación y se diferencian en el punto de corte con el eje de ordenadas. | ||
| + | {{p}} | ||
| + | 5. Para esta gráfica que corta al eje de ordenadas en 5, la fórmula que expresa la relación entre el volumen y el tiempo es: | ||
| - | [[Imagen:afin1.jpg]] | + | {{Caja|contenido=<math>V=5 \cdot t+5</math>}} |
| + | }} | ||
| {{p}} | {{p}} | ||
| {{AI2|titulo=Actividades Interactivas: ''Función lineal afín''|cuerpo= | {{AI2|titulo=Actividades Interactivas: ''Función lineal afín''|cuerpo= | ||
Revisión de 11:52 6 dic 2008
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Proporcionalidad directa | Ejercicios Ecuación pto-pendiente Ecuaciones de la recta | WIRIS Geogebra Calculadora Función lineal Recta |
Función lineal afín
Una función lineal afín es aquella cuya expresión matemática viene dada por:
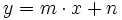
donde  e
e  son variables,
son variables, 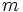 una constante que se denomina pendiente y
una constante que se denomina pendiente y  otra constante denominada ordenada en el origen. Su gráfica es una recta que corta al eje de ordenadas en
otra constante denominada ordenada en el origen. Su gráfica es una recta que corta al eje de ordenadas en  .
.
Ejemplos: Función lineal afín
- Un estanque tiene un grifo que vierte 5 litros por minuto. Haz una tabla que relacione el tiempo transcurrido (en minutos) y el volumen (en litros) de estanque que se llena. Escribe la fórmula que relaciona el volumen y el tiempo. Representa gráficamente los resultados.
- Repite el apartado anterior suponiendo que el estanque tiene un volumen inicial de 20 litros.
- ¿Y si partiésemos de un volumen inicial de 10 litros, cuáles serían los resultados?
- Compara las gráficas obtenidas e indica que tienen en común y en qué se diferencian.
- ¿Qué fórmula correspondería a esta situación gráfica?
| 2. Supongamos ahora que el estanque tiene inicialmente un volumen de 20 litros.
Completa la tabla:
La fórmula que expresa la relación entre el volumen y el tiempo ahora es:
| 
|
| 3. Ahora supondremos que el estanque tiene inicialmente un volumen de 10 litros.
Completa la tabla:
La fórmula que expresa la relación entre el volumen y el tiempo ahora es:
| 
|
4. Las graficas son rectas paralelas que cortan al eje de ordenadas a una altura que coincide con el volumen inicial del estanque. Por tanto, tienen en común que tienen la misma inclinación y se diferencian en el punto de corte con el eje de ordenadas.
5. Para esta gráfica que corta al eje de ordenadas en 5, la fórmula que expresa la relación entre el volumen y el tiempo es:
|
|
|
Actividades Interactivas: Función lineal afín
1. Función constante y otros ejemplos de funciones lineales afines.
Actividad:
En la siguiente escena aparece la función y = 3, llamada función constante 3, porque su valor no cambia; a cada valor de x le corresponde siempre el valor 3. Mueve el punto rojo y comprueba que el valor de la ordenada siempre es 3. a) Varia ahora el valor de k con los pulsadores o escribiendo su valor y pulsando "intro". Obtienes la función y = k ¿Cuánto vale la pendiente de todas estas rectas?.
En la siguiente escena vamos a comparar la función y = 2x y la y = 2x + 3. b) ¿Que parecidos y diferencias encuentras entre las funciones y = 2x e y = 2x + 3? c) Cambia el valor de k con los pulsadores o escribiendo su valor y pulsando "intro" y explica como afecta el valor de k en el aspecto de la gráfica y = 2x + k. ¿Cuánto vale la pendiente de todas estas rectas?. d) Pulsa el boton inicio para reestablecer los valores iniciales. Cambia el valor de m con los pulsadores o escribiendo su valor y pulsando "intro" y explica como afecta el valor de m en el aspecto de la gráfica y = mx + 3. ¿Cuánto vale la ordenada en el origen de todas estas rectas?.
2. Cálculo de la pendiente y de la ordenada en el origen.
Actividad:
En esta escena puedes ver un método para calcular la pendiente de una recta cualquiera. Mueve el punto rojo y comprueba que para cualquier punto que no esté sobre la recta el cociente entre los segmentos señalados (verde y azul) permanece constante y es igual a la pendiente. Así: 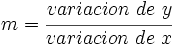 a) Varia ahora el valor de m y de k con los pulsadores o escribiendo su valor y pulsando "intro" para hallar la pendiente de las siguientes rectas:
a)
En esta escena puedes ver el segmento que representa la ordenada en el origen de una recta. Cambia el valor de m y k. Observa el segmento amarillo que representa el valor de k y no depende, por tanto de m. El parámetro k se llama ordenada en el origen de la función afín porque indica el valor de la función cuando x vale cero. Comprueba que las rectas que pasan por el mismo punto del eje Y, tienen el mismo valor de k y se diferencian sólo en su pendiente.
3. Halla la ecuación de la recta a partir de su gráfica.
Actividad: Se trata de determinar la pendiente y la ordenada en el origen de una recta cualquiera, que son los elementos que se necesitan para escribir la ecuación. a) Tienes que escribir los valores de m y k para determinar la ecuación de la recta azul. Ayúdate del zoom para poder ver los puntos por los que pasa la recta. Para dar valores a m y k puedes escribir números decimales o fracciones como 5/7 ó -1/2 y pulsar la tecla Intro. El pulsador azul de la ayuda la activa y el rojo la desactiva. Con la ayuda activada no se cuentan los aciertos. Si aciertas verás la expresión de la función con color azul, si no aciertas verás la recta correspondiente de color rojizo. Después de cada acierto pulsa el botón animar para que se salga una nueva recta. |
Ejercicios
|
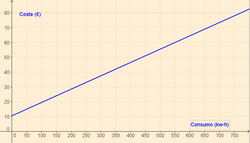
Ejercicio: Función afín 1. La factura de la luz que hemos contratado en casa nos supone un coste de 10,44 €, además de 0,09 € por kilovatio-hora consumido.
|






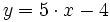 b)
b) 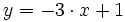 c)
c) 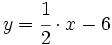 Anota los resultados en tu cuaderno.
Anota los resultados en tu cuaderno.