Números enteros
De Wikipedia
| Revisión de 17:55 14 abr 2007 Coordinador (Discusión | contribuciones) (→Propiedades) ← Ir a diferencia anterior |
Revisión de 09:59 15 abr 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| {{Menú Matemáticas 3ESO | {{Menú Matemáticas 3ESO | ||
| |titulo=NUMEROS ENTEROS | |titulo=NUMEROS ENTEROS | ||
| - | |ir=[[Matemáticas 3º E.S.O.|Indice]]<br> | + | |ir= |ampliar=[http://es.wikipedia.org/wiki/Numeros_enteros Números enteros] |
| - | |ampliar=[http://es.wikipedia.org/wiki/Numeros_enteros Números enteros] | + | |
| |repasar= | |repasar= | ||
| [http://descartes.cnice.mecd.es/1y2_eso/enteros1/index.htm Números enteros I]<br> | [http://descartes.cnice.mecd.es/1y2_eso/enteros1/index.htm Números enteros I]<br> | ||
| [http://descartes.cnice.mecd.es/1y2_eso/enteros2/index.htm Números enteros II] | [http://descartes.cnice.mecd.es/1y2_eso/enteros2/index.htm Números enteros II] | ||
| - | |herramientas=[http://herramientas.educa.madrid.org/wiris/ WIRIS]<br>[http://world.casio.com/calc/download/es/manual/ Calculadora] | + | |herramientas=}}{{p}} |
| - | }}{{p}} | + | |
| ==Definición== | ==Definición== | ||
| El conjunto de los '''números enteros''' es <math>\mathbb{Z}=\left \lbrace \cdots, -3, -2,-1,\ 0,\ 1 ,\ 2,\ 3, \cdots \right \rbrace</math>. Son infinitos y, al igual que los [[números naturales]] sirven para contar. Sin emabrgo, los números enteros permiten expresar cantidades negativas como un saldo deudor en una cuenta bancaria, un año de la era antes de Cristo, el número de una planta del sótano de un edificio, etc. | El conjunto de los '''números enteros''' es <math>\mathbb{Z}=\left \lbrace \cdots, -3, -2,-1,\ 0,\ 1 ,\ 2,\ 3, \cdots \right \rbrace</math>. Son infinitos y, al igual que los [[números naturales]] sirven para contar. Sin emabrgo, los números enteros permiten expresar cantidades negativas como un saldo deudor en una cuenta bancaria, un año de la era antes de Cristo, el número de una planta del sótano de un edificio, etc. | ||
Revisión de 09:59 15 abr 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Números enteros I | Números enteros | WIRIS Geogebra Calculadora {{{enlaces}}} |
Tabla de contenidos |
Definición
El conjunto de los números enteros es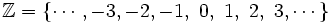 
. Son infinitos y, al igual que los números naturales sirven para contar. Sin emabrgo, los números enteros permiten expresar cantidades negativas como un saldo deudor en una cuenta bancaria, un año de la era antes de Cristo, el número de una planta del sótano de un edificio, etc.
Podemos representarlos en una recta:
Orden
En el gráfico anterior se observa el orden que existe en el conjunto de los números enteros, siendo los números negativos menores que los positivos y que el cero. Se cumple que:
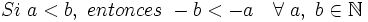
Operaciones
Valor absoluto
Opuesto
Suma
Uso del paréntesis
Actividad Interactiva: Uso del paréntesis
Multiplicación
Regla de los signos
Propiedades
La suma y multiplicación de números enteros cumplen, al igual que los números naturales, las propiedades asociativa, conmutativa y distributiva. La propiedad distributiva sirve para simplificar expresiones sacando factor común. Veamos un ejemplo
Ejemplo: Sacar factor común
- Saca factor común en la expresión 36a3 − 24a2 + 6a
El factor común, que se repite en los tres sumandos, es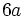 
. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común 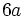, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
