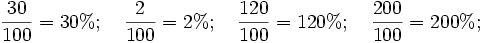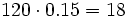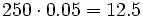Cálculos con porcentajes (3ºESO Académicas)
De Wikipedia
| Revisión de 13:29 13 sep 2016 Coordinador (Discusión | contribuciones) (→Porcentaje correspondiente a una proporción) ← Ir a diferencia anterior |
Revisión de 13:32 13 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 15: | Línea 15: | ||
| ===Tanto por ciento de una cantidad=== | ===Tanto por ciento de una cantidad=== | ||
| {{calculo del porcentaje}} | {{calculo del porcentaje}} | ||
| + | {{p}} | ||
| + | ===Cálculo de la cantidad total a partir del porcentaje=== | ||
| + | {{porcentaje inverso}} | ||
| {{p}} | {{p}} | ||
| ===Porcentaje correspondiente a una proporción=== | ===Porcentaje correspondiente a una proporción=== | ||
| {{porcentaje de proporcion}} | {{porcentaje de proporcion}} | ||
| {{p}} | {{p}} | ||
| - | ===Cálculo de la cantidad total a partir del porcentaje=== | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Cálculo de la cantidad total a partir del porcentaje'' | ||
| - | |enunciado= | ||
| - | :Si en una clase hay 5 alumnos rubios, y representan el 20% de la clase, ¿cuántos alumnos hay en total? | ||
| - | |sol= | ||
| - | '''Método 1: A partir de la definición de pordentaje:''' | ||
| - | |||
| - | Si llamamos <math>C\;\!</math> al total de alumnos de la clase: | ||
| - | |||
| - | <center><math>5=\frac{20}{100} \cdot C </math></center> | ||
| - | |||
| - | Y despejando <math>C\;\!</math>: | ||
| - | |||
| - | <center><math>C=\frac{5 \cdot 100}{20}= 25 \ alumnos</math></center> | ||
| - | |||
| - | '''Método 2: Mediante una regla de tres''' | ||
| - | |||
| - | 20% ----> 5 alumnos | ||
| - | 100% ----> x alumnos | ||
| - | |||
| - | Y despejando <math>x\;\!</math>: | ||
| - | |||
| - | <center><math>x=\frac{5 \cdot 100}{20}= 25 \ alumnos</math></center> | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
Revisión de 13:32 13 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 50)
Porcentajes
- Un porcentaje es una razón entre un número n y 100 y representa las partes que tomamos de un total de 100.
- Se representa escribiendo el número seguido del símbolo %, esto es:
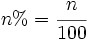 (se lee "
(se lee " por ciento")
por ciento")Colorea el 20% de un cuadrado.
Colorea el 109% de un cuadrado.
Actividades para aprender y practicar con el significado de los porcentajes. Los porcentajes podemos verlos como fracción o como número decimal.
Actividades para aprender y practicar con el significado de los porcentajes. Los porcentajes podemos verlos como fracción o como número decimal.
Introducción a los porcentajes.
Porcentajes a partir de modelos de fracciones.
Relaciona fracciones, decimales y porcentajes.
Conversión entre porcentajes, fracciones y decimales
Hemos definido un porcentaje como una fracción y sabemos que una fracción se puede escribir como un número decimal. Por tanto, un porcentaje lo podemos expresar de tres formas equivalentes: como porcentaje, como fracción o como número decimal.
Convierte el decimal 0.601 a un porcentaje equivalente.
Convierte el decimal 1.501 a un porcentaje equivalente.
Convierte 59.2% en un decimal equivalente.
Convierte 113.9% en un decimal equivalente.
Convierte 18% en un decimal y en una fracción equivalente.
Conversión entre porcentajes, fracciones y decimales.
Repaso de conversión entre decimales y porcentajes.
Repaso de conversión entre porcentajes y fracciones.
Convertir decimales en porcentajes.
Convertir porcentajes en decimales.
Convertir porcentajes y fracciones.
Tanto por ciento de una cantidad
Cálculo del porcentaje
Para hallar el 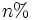 de una cantidad,
de una cantidad, 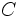 , podemos proceder de dos formas:
, podemos proceder de dos formas:
- Calculando la fracción de dicha cantidad:
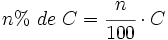
- Mediante una proporción (regla de tres directa):
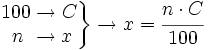
Ejemplo: Cálculo de porcentajes (2 métodos)
En un pueblo hay 2000 habitantes, de los cuales el 16% son niños. ¿Cuántos niños hay en el pueblo?
Método 1: A partir de la definición de porcentaje:
- El 16% de 2000
 niños
niños
Método 2: Mediante una regla de tres:
100% ----> 2000
16% ----> x
| 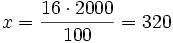 niños niños
|
Cálculo rápido de un porcentaje
Hemos visto que un porcentaje es equivalente a una razón de divisor 100, y dividir entre 100 es muy fácil (basta correr la coma decimal dos lugares a la izquierda). Así, si transformamos esa razón en un número decimal mentalmente, el cálculo del tanto por ciento se reduce a una simple multiplicación.
Cálculo rápido de un porcentaje
Calcular el n% de una cantidad equivale a multiplicar la cantidad por el número que resulta de dividir n entre 100.
Cálculo del procentaje de un número. Ejemplos.
Tutorial en el que se dan los conceptos matemáticos de proporción y porcentaje, viendo la información que aporta cada uno de ellos y cómo pasar de una forma a otra.
Definición de tanto por ciento. Ejemplos.
Definición de tanto por ciento. Ejemplos.
Definición de tanto por ciento. Ejemplos.
¿Cuál es el 12% de 75?
¿Cuál es el 30% de 6?
Gasté el 30% de mi dinero y regalé el 16% de lo que me quedó. Si al principio tenía 250€, ¿cuánto tengo ahora?
Problemas de cálculo del porcentajes por el método directo.
Calcula los siguientes porcentajes en tu cuaderno y luego comprueba los resultados en la escena.
- a) 10% de 43; b) 60% de 200; c) 50% de 40; d) 5% de 1000; e) 25% de 400.
Porcentajes sencillos
Hay algunos porcentajes que se pueden calcular fácilmente:
Procedimiento
- Calcular el 10% equivale a dividir por 10.
- Calcular el 20% equivale a dividir por 5.
- Calcular el 25% equivale a dividir por 4.
- Calcular el 50% equivale a dividir por 2.
Calcula mentalmente:
¿Qué resultado es el correcto? Pincha con el ratón el punto rojo y llévalo a la caja del número que te parezca correcto. Para hacer otro ejercicio pulsa el botón inicio
Cálculo de la cantidad total a partir del porcentaje
Ejemplo: Cálculo de la cantidad total a partir del porcentaje (porcentaje inverso)
Si en una clase hay 5 alumnos rubios, y representan el 20% de la clase, ¿cuántos alumnos hay en total?
Método 1: A partir de la definición de porcentaje:
Si llamamos 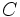 al total de alumnos de la clase:
al total de alumnos de la clase:
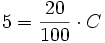
Y despejando 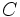 :
:
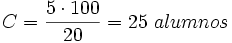
Método 2: Mediante una regla de tres
% alumnos
---- -------
Parte: 20 ----> 5
Total: 100 ----> x
Y despejando  :
:
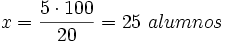
Cálculo del total conocida una parte y el porcentaje. Ejemplos.
Tutorial en el que se dan los conceptos matemáticos de porcentajes y se explica/justifica como calcular porcentajes de cantidades o bien la cantidad a la que se le aplicó una proporción.
¿De qué número es 300 el 40%?
¿De qué número es 150 el 25%?
¿De qué número es 78 es el 15%?
Hoy las guayabas estaban rebajadas un 30% en el mercado y por 6 unidades pagué $12.60. ¿Cuánto habría pagado por 2 guayabas si no hubiesen estado rebajadas?
Un zoológico tiene 15 pingüinos emperador que constituyen el 30% del total de pingüinos del zoológico. ¿Cuántos pingüinos hay en el zoológico?
Actividades en las que practicarás el cálculo del total conocida una parte y el porcentaje (porcentaje inverso), y de la parte conocido el total y el porcentaje (porcentaje directo).
Actividades de autoevaluación sobre cálculo de porcentajes inversos.
Porcentaje correspondiente a una proporción
Procentaje correspondiente a una proporción
Para hallar qué tanto por ciento representa una cantidad,  , repecto a un total,
, repecto a un total, 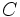 , se efectúa la siguiente operación:
, se efectúa la siguiente operación:
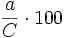
Ejemplo: Porcentaje correspondiente a una proporción
En un grupo del instituto, de 30 alumnos aprueban 21. ¿Qué porcentaje del total representan los aprobados?. ¿Y los suspensos?
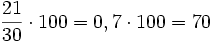
Por tanto el 70% aprueban y el 30% suspenden.
También podemos hacerlo mediante una regla de tres:
% alumnos
---- -------
Total: 100 ----> 30
Parte (aprobados): x ----> 21
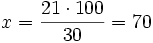
Cálculo del porcentaje conocida una parte y el total. Ejemplos.
¿Qué porcentaje es 425 de 500?
¿Qué porcentaje de 16 es 4?
¿Qué porcentaje es 100 de 80?
Un hotel tiene 300 habitaciones de las que 60 están vacías. ¿Cua´l es el porcentaje de ocupación?
En México 13 de cada 20 latas son recicladas. ¿Qué porcentaje de latas es reciclado?
Actividades en las que practicarás el cálculo del porcentaje conocida una parte y el total.
Actividades de autoevaluación sobre cálculo del porcentaje a partir de la parte y el total.
Ejercicios propuestos
|
Ejercicios propuestos: Porcentajes |
(Pág. 51)
Aumentos y disminuciones porcentuales
Aumentos porcentuales
Disminuciones porcentuales
Ejercicios propuestos
|
Ejercicios propuestos: Aumentos y disminuciones porcentuales |
(Pág. 52)
Cálculo de la cantidad inicial tras un incremento/disminución porcentual
Ejercicios propuestos
|
Ejercicios propuestos: Cálculo de la cantidad inicial |
(Pág. 53)
Encadenamientos porcentuales
Ejercicios propuestos
|
Ejercicios propuestos: Encadenamientos porcentuales |