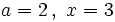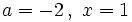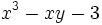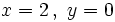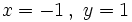Expresiones algebraicas
De Wikipedia
| Revisión de 12:12 24 oct 2016 Coordinador (Discusión | contribuciones) (→Valor numérico de una expresión algebraica) ← Ir a diferencia anterior |
Revisión de 16:15 24 oct 2016 Coordinador (Discusión | contribuciones) (→Expresiones algebraicas) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| Las expresiones algebraicas nos permiten traducir al lenguaje matemático expresiones del lenguaje habitual. | Las expresiones algebraicas nos permiten traducir al lenguaje matemático expresiones del lenguaje habitual. | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Expresión algebraica'' | + | {{Ejemplo|titulo=Ejemplos: ''Expresiones algebraicas'' |
| |enunciado= | |enunciado= | ||
| Expresa mediante expresiones algebraicas: | Expresa mediante expresiones algebraicas: | ||
Revisión de 16:15 24 oct 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Algebra (1º ESO) | WIRIS Geogebra Calculadora |
Expresiones algebraicas
- Una expresión algebraica es cualquier combinación de letras y números ligados por las operaciones elementales de suma, resta, multiplicación, división, potenciación y radicación.
- Las letras, que suelen representar cantidades desconocidas, se denominan variables o incógnitas y los números coeficientes.
Las expresiones algebraicas nos permiten traducir al lenguaje matemático expresiones del lenguaje habitual.
Ejemplos: Expresiones algebraicas
Expresa mediante expresiones algebraicas:
- a) El doble de un número menos cuatro unidades.
- b) La mitad de sumarle 5 al triple de un número.
- c) El perímetro y el área de un terreno rectangular.
a) Si llamamos  al número, entonces el doble del número menos cuatro unidades es
al número, entonces el doble del número menos cuatro unidades es 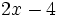 .
.
b) Llamando  al número, la mitad de sumarle 5 al triple de dicho número es
al número, la mitad de sumarle 5 al triple de dicho número es 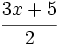
c) Si suponemos que el terreno rectangular mide  de largo e
de largo e  de ancho, tenemos:
de ancho, tenemos:
- Perimetro:
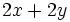
- Area:
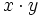
Tipos de expresiones algebraicas
Hay distintos tipos de expresiones algebraicas.
- Dependiendo del número de sumandos, tenemos: monomios (1 sumando) y polinomios (varios sumandos).
- Algunos polinomios tienen nombre propio: binomio (2 sumandos), trinomio (3 sumandos), ...
- Dos expresiones algebraicas separadas por un signo
 reciben el nombre de ecuación.
reciben el nombre de ecuación.
- Un caso particular de ecuación es la identidad, en la que los dos lados de la igualdad son equivalentes.
- Monomios:
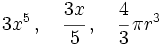
- Polinomios:
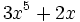 (binomio),
(binomio), 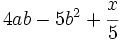 (trinomio)
(trinomio)
- Ecuaciones:
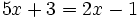
- Identidades:
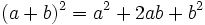
Valor numérico de una expresión algebraica
Si en una expresión algebraica se sustituyen las letras por números y se realiza la operación indicada se obtiene un número que es el valor númerico de la expresión algebraica para los valores de las letras dados.
Ejemplo: Valor numérico de una expresión algebraica
a) Halla el valor numérico del polinomio 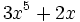 para
para 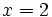
b) Halla el valor numérico del polinomio 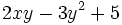 para
para 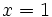 e
e 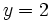 .
.
a) El valor numérico del polinomio es: 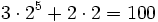
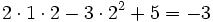
|
Actividad Interactiva: Valor numérico de una expresión algebraica
1. Calcula el valor numérico del polinomio
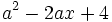 en los casos: en los casos:
a) b)  y y  que hagan que el valor numérico valga cero. que hagan que el valor numérico valga cero.Actividad: Haz los cálculos en tu cuaderno y compruébalos posteriormente en la siguiente escena: |
|
Actividad: Valor numérico de una expresión algebraica Calcula el valor numérico del polinomio
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|