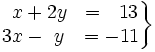Sistemas de ecuaciones lineales (3ºESO Académicas)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:10 30 oct 2016 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) ← Ir a diferencia anterior |
Revisión de 17:14 30 oct 2016 Coordinador (Discusión | contribuciones) (→Método grafico de resolución de sistemas de ecuaciones lineales 2x2) Ir a siguiente diferencia → |
||
| Línea 23: | Línea 23: | ||
| {{p}} | {{p}} | ||
| - | ==Método grafico de resolución de sistemas de ecuaciones lineales 2x2== | ||
| - | {{Método grafico de resolución de sistemas de ecuaciones lineales 2x2}} | ||
| - | {{p}} | ||
| - | ===Ejercicios propuestos=== | ||
| - | {{ejercicio | ||
| - | |titulo=Ejercicios propuestos: ''Sistemas de ecuaciones lineales'' | ||
| - | |cuerpo= | ||
| - | (Pág. 124) | ||
| - | [[Imagen:red_star.png|12px]] 2 | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión de 17:14 30 oct 2016
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 125)
Sistemas de ecuaciones lineales 2x2
- Un sistema de dos ecuaciones de primer grado con dos incógnitas o simplemente, sistema 2x2 de ecuaciones lineales, es la agrupación de dos ecuaciones de primer grado con dos incógnitas:
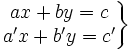
- Se llama solución de un sistema 2x2, a cualquier pareja de valores
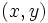que sea solución de ambas ecuaciones a la vez. Las soluciones de este tipo de sistemas son los puntos de corte de las rectas que representan cada una de las ecuaciones del sistema.
Ejemplo: Solución de un sistema de ecuaciones
Comprueba si las parejas de números (1,2) y (-1,3) son o no soluciones del sistema:
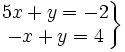
Solución:
- Para comprobar si (1,2) es solución, sustituimos x=1 e y=2 en las dos ecuaciones del sistema:
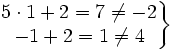
Como no se verifican las dos ecuaciones, la pareja (1,2) no es solución del sistema.
- Para comprobar si (-1,3) es solución, sustituimos x=-1 e y=3 en las dos ecuaciones del sistema:
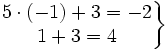
Autoevaluación 1 Descripción: Ejercicios de autoevaluación sobre sistemas de ecuaciones lineales.
Autoevaluación 2 Descripción: Comprueba soluciones de sistemas de ecuaciones lineales.
Ejercicios propuestos
 Ejercicios propuestos: Sistemas de ecuaciones lineales (Pág. 125)
|
