Plantilla:Función inversa (1ºBach)
De Wikipedia
| Revisión de 11:28 13 dic 2016 Coordinador (Discusión | contribuciones) (→Obtención de la expresión analítica de la función inversa) ← Ir a diferencia anterior |
Revisión de 11:07 19 abr 2017 Coordinador (Discusión | contribuciones) (→Obtención de la expresión analítica de la función inversa) Ir a siguiente diferencia → |
||
| Línea 33: | Línea 33: | ||
| #Se intercambian las dos incógnitas (donde aparece "x" se pone "y" y viceversa). | #Se intercambian las dos incógnitas (donde aparece "x" se pone "y" y viceversa). | ||
| #La expresión resultante es la de la función inversa de f. | #La expresión resultante es la de la función inversa de f. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace2 | ||
| + | |titulo1=Obtención de la expresión analítica de la función inversa. | ||
| + | |duracion=13'30" | ||
| + | |sinopsis=Algunos ejemplos sobre el cáculo de la función inversa y sobre la composición de funciones. | ||
| + | |url1=http://www.unicoos.com/clase/matematicas/1-bachiller/funciones/composicion-de-funciones/composicion-de-funciones-y-funcion-inversa | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 11:07 19 abr 2017
Función inversa o recíproca
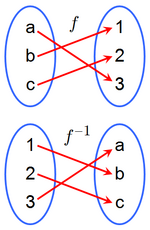
Si  es una función que lleva elementos de es una función que lleva elementos de 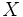 en elementos de en elementos de 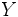 , en ciertas condiciones será posible definir la aplicación , en ciertas condiciones será posible definir la aplicación 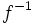 que realice el camino de vuelta de que realice el camino de vuelta de 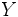 a a 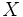 . En ese caso diremos que . En ese caso diremos que 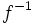 es la función inversa o recíproca de es la función inversa o recíproca de  . Formalmente: . Formalmente:
Propiedades Sea
donde |
Obtención de la expresión analítica de la función inversa
Procedimiento
Para intentar hallar la expresión analítica de la inversa de y=f(x):
- Se despeja (si se puede) la variable "x" para ponerla en función de la variable "y".
- Se intercambian las dos incógnitas (donde aparece "x" se pone "y" y viceversa).
- La expresión resultante es la de la función inversa de f.
Algunos ejemplos sobre el cáculo de la función inversa y sobre la composición de funciones.
Ejemplo: Función inversa
Halla la función inversa de la función 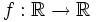 definida por
definida por  :
:
Como la función  no es inyectiva, no podemos calcular su inversa. No obstante, podemos descomponerla en dos trozos que si sean funciones inyectivas por separado y a los que si podamos calcular su inversa:
no es inyectiva, no podemos calcular su inversa. No obstante, podemos descomponerla en dos trozos que si sean funciones inyectivas por separado y a los que si podamos calcular su inversa:
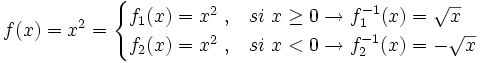
En la siguiente escena puedes ver  (en verde),
(en verde), 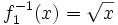 (en amarillo), y
(en amarillo), y 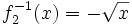 (en turquesa):
(en turquesa):
En esta escena podrás introducir la expresión analítica de una función y obtener la expresión analítica de su inversa, así como ver sus respectivas representaciones gráficas. También se te propondrán algunas actividades.
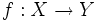 es
es 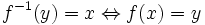
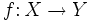 una función y
una función y 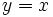 .
.
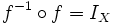

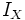 e
e 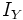 son las
son las