Cuadriláteros (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:12 19 jul 2017 Coordinador (Discusión | contribuciones) (→Clasificación de los cuadriláteros) ← Ir a diferencia anterior |
Revisión de 07:21 20 jul 2017 Coordinador (Discusión | contribuciones) (→Diagonales y ejes de simetría de los paralelogramos) Ir a siguiente diferencia → |
||
| Línea 58: | Línea 58: | ||
| ==Diagonales y ejes de simetría de los paralelogramos== | ==Diagonales y ejes de simetría de los paralelogramos== | ||
| - | {{Teorema_sin_demo|titulo=Propiedades|enunciado= | + | {{Tabla75|celda2=[[Imagen:diag_paralelogramos.jpg]] |
| - | '''Diagonales:''' | + | |celda1={{Teorema_sin_demo|titulo=Propiedades|enunciado= |
| *Las diagonales de un paralelogramo se cortan en sus puntos medios. | *Las diagonales de un paralelogramo se cortan en sus puntos medios. | ||
| *Las diagonales del cuadrado y del rombo son perpendiculares. | *Las diagonales del cuadrado y del rombo son perpendiculares. | ||
| *Las diagonales del cuadrado y del rectángulo son iguales. | *Las diagonales del cuadrado y del rectángulo son iguales. | ||
| - | + | }} | |
| - | '''Ejes de simetría:''' | + | }} |
| + | {{p}} | ||
| + | ==Ejes de simetría de los paralelogramos== | ||
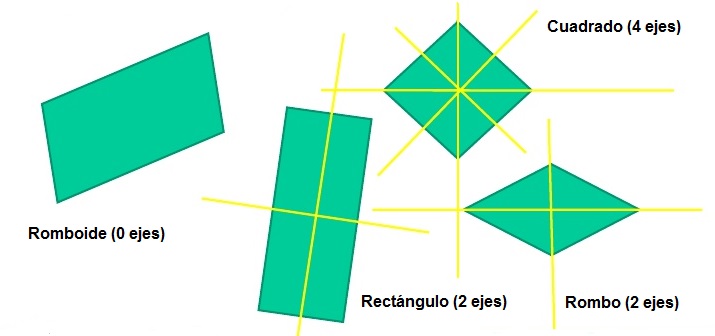
| + | {{Tabla75|celda2=[[Imagen:simetrias_paralelogramos.jpg]] | ||
| + | |celda1={{Teorema_sin_demo|titulo=Propiedades|enunciado= | ||
| *El romboide no tiene ejes de simetría. | *El romboide no tiene ejes de simetría. | ||
| *El rectángulo y el rombo no tienen ejes de simetría. | *El rectángulo y el rombo no tienen ejes de simetría. | ||
| *El cuadrado tiene cuatro ejes de simetría. | *El cuadrado tiene cuatro ejes de simetría. | ||
| + | }} | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 07:21 20 jul 2017
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Cuadrilátero
Propiedades
Todo cuadrilátero cumple las siguientes propiedades:
- Sus cuatro ángulos suman 360º.
- Tienen dos diagonales.
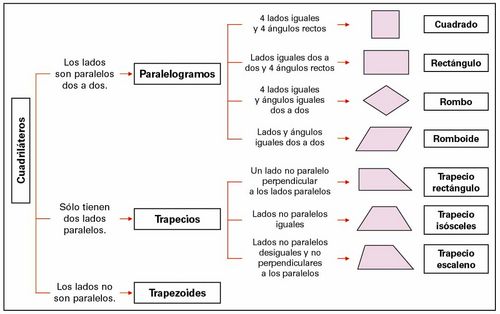
Clasificación de los cuadriláteros
Los cuadriláteros se clasifican, atendiendo al paralelismo de sus lados, en:
Los paralelogramos se clasifican, atendiendo a sus lados y a sus ángulos, en:
Los trapecios se clasifican en:
|  |
Cuadriláteros: Elementos y clasificación Descripción: Actividades en las que podrás aprender el concepto de cuadrilátero, identificar sus elementos y clasificar los cuadriláteros atendiendo al número de lados paralelos que poseen.
Clasificación de los paralelogramos Descripción: Actividades en las que podrás aprender los distintos tipos de paralelogramos.
Diagonales y ejes de simetría de los paralelogramos
Propiedades
| 
|
Ejes de simetría de los paralelogramos
Propiedades
| 
|
