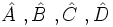Cuadriláteros (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:57 20 jul 2017 Coordinador (Discusión | contribuciones) (→Cuadrilátero) ← Ir a diferencia anterior |
Revisión de 08:14 20 jul 2017 Coordinador (Discusión | contribuciones) (→Cuadrilátero) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| ==Cuadrilátero== | ==Cuadrilátero== | ||
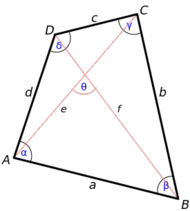
| - | {{Tabla75|celda2=[[Imagen:cuadrilatero.png|center|200px]]|celda1= | + | {{Tabla75|celda2=[[Imagen:cuadrilatero.png|center|190px|thumb|'''Cuadrilátero:''' Tiene dos diagonales: ''e'' y ''f''; Sus ángulos suman 360º: α+β+γ+δ=360º.]]|celda1= |
| {{Caja_Amarilla|texto=Un '''cuadrilátero''' es un [[Polígonos (1º ESO)|polígono]] de cuatro [[Polígonos (1º ESO)#Polígono|lados]].}} | {{Caja_Amarilla|texto=Un '''cuadrilátero''' es un [[Polígonos (1º ESO)|polígono]] de cuatro [[Polígonos (1º ESO)#Polígono|lados]].}} | ||
| {{p}} | {{p}} | ||
| Línea 16: | Línea 16: | ||
| #Sus cuatro [[ángulos]] suman 360º. | #Sus cuatro [[ángulos]] suman 360º. | ||
| #Tienen dos diagonales. | #Tienen dos diagonales. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Caja_gris|texto= | ||
| + | '''Nomenclatura:''' | ||
| + | *Observa en la figura adjunta como se nombran los vértices con letras mayúsculas (A, B, C, D) y los lados con minúsculas (a, b, c, d) y como aparecen dispuestos de forma consecutiva siguiendo el sentido contrario de las agujas del reloj. | ||
| + | *Para los ángulos se utilizan letras griegas (α, β, γ, δ), pero también se pueden representar por {{sube|porcentaje=20%|contenido=<math>\hat A \ , \hat B \ , \hat C \ , \hat D</math>}} | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 08:14 20 jul 2017
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Cuadrilátero
|
Propiedades Todo cuadrilátero cumple las siguientes propiedades:
Nomenclatura:
|
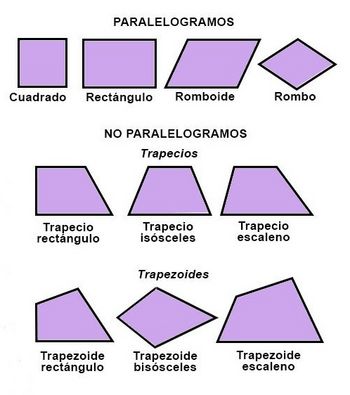
Clasificación de los cuadriláteros
Los cuadriláteros se clasifican, atendiendo al paralelismo de sus lados, en:
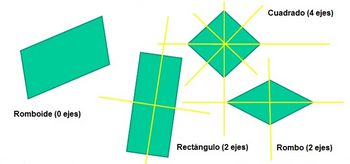
Los paralelogramos se clasifican, atendiendo a sus lados y a sus ángulos, en:
Los trapecios se clasifican en:
|
Actividades en las que podrás aprender el concepto de cuadrilátero, identificar sus elementos y clasificar los cuadriláteros atendiendo al número de lados paralelos que poseen.
Actividades en las que podrás aprender los distintos tipos de paralelogramos.