Números racionales
De Wikipedia
| Revisión de 13:35 27 may 2007 Coordinador (Discusión | contribuciones) (→Operaciones con fracciones) ← Ir a diferencia anterior |
Revisión de 18:35 25 jun 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 22: | Línea 22: | ||
| {{AI2|titulo=Actividades Interactivas: ''Fracciones''|cuerpo= | {{AI2|titulo=Actividades Interactivas: ''Fracciones''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=1. Concepto de fracción. | + | |enunciado='''Actividad 1:''' Concepto de fracción. |
| |actividad= | |actividad= | ||
| Línea 33: | Línea 33: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=2. ¿Qué fracción representa cada figura? | + | |enunciado='''Actividad 2:''' ¿Qué fracción representa cada figura? |
| |actividad= | |actividad= | ||
| Línea 44: | Línea 44: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=3. Representación de las fracciones en la recta numérica. | + | |enunciado='''Actividad 3:''' Representación de las fracciones en la recta numérica. |
| |actividad= | |actividad= | ||
| Línea 56: | Línea 56: | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=4. Adivina la posición de cada fracción en la recta numérica. | + | |enunciado='''Actividad 4:''' Adivina la posición de cada fracción en la recta numérica. |
| |actividad= | |actividad= | ||
| Línea 73: | Línea 73: | ||
| {{AI2|titulo=Actividades Interactivas: ''Fracciones propias e impropias''|cuerpo= | {{AI2|titulo=Actividades Interactivas: ''Fracciones propias e impropias''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=1. Definición de fracción propia e impropia. | + | |enunciado='''Actividad 1:''' Definición de fracción propia e impropia. |
| |actividad= | |actividad= | ||
| Línea 84: | Línea 84: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=2. Separa las fracciones propias de las impropias. | + | |enunciado='''Actividad 2:''' Separa las fracciones propias de las impropias. |
| |actividad= | |actividad= | ||
| Puesto que una fracción representa una división, para saber cuál es el valor de una fracción deberíamos realizar esa división, no obstante, podemos apreciar el valor de una fracción si nos fijamos en su numerador y su denominador. | Puesto que una fracción representa una división, para saber cuál es el valor de una fracción deberíamos realizar esa división, no obstante, podemos apreciar el valor de una fracción si nos fijamos en su numerador y su denominador. | ||
| Línea 117: | Línea 117: | ||
| {{AI2|titulo=Actividades Interactivas: ''Fracciones equivalentes''|cuerpo= | {{AI2|titulo=Actividades Interactivas: ''Fracciones equivalentes''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=1. Definición de fracciones equivalentes. | + | |enunciado='''Actividad 1:''' Definición de fracciones equivalentes. |
| |actividad= | |actividad= | ||
| Línea 128: | Línea 128: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=2. Busca una fracción equivalente a la dada. | + | |enunciado='''Actividad 2:''' Busca una fracción equivalente a la dada. |
| |actividad= | |actividad= | ||
| En la siguiente escena, escribe el numerador y denominador de otra fracción equivalente a ella y pulsa "intro" o usa los pulsadores. | En la siguiente escena, escribe el numerador y denominador de otra fracción equivalente a ella y pulsa "intro" o usa los pulsadores. | ||
| Línea 143: | Línea 143: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=3. Comprueba si dos fracciones son equivalentes o no (Método de los productos cruzados). | + | |enunciado='''Actividad 3:''' Comprueba si dos fracciones son equivalentes o no (Método de los productos cruzados). |
| |actividad= | |actividad= | ||
| Para comprobar si dos fracciones son equivalentes o no, el método más fácil es el de los productos cruzados. | Para comprobar si dos fracciones son equivalentes o no, el método más fácil es el de los productos cruzados. | ||
| Línea 162: | Línea 162: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=4. Junta las fracciones equivalentes. | + | |enunciado='''Actividad 4:''' Junta las fracciones equivalentes. |
| |actividad= | |actividad= | ||
| Cada fracción de abajo es equivalente a otra de arriba. Colócala junto a ella. | Cada fracción de abajo es equivalente a otra de arriba. Colócala junto a ella. | ||
| Línea 177: | Línea 177: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=5. Agrupa las fracciones equivalentes. | + | |enunciado='''Actividad 5:''' Agrupa las fracciones equivalentes. |
| |actividad= | |actividad= | ||
| Línea 195: | Línea 195: | ||
| {{AI2|titulo=Actividades Interactivas: ''Simplificación de fracciones''|cuerpo= | {{AI2|titulo=Actividades Interactivas: ''Simplificación de fracciones''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=1. Simplifica las fracciones. | + | |enunciado='''Actividad 1:''' Simplifica las fracciones. |
| |actividad= | |actividad= | ||
| Todas las fracciones equivalentes entre sí representan el mismo número racional. | Todas las fracciones equivalentes entre sí representan el mismo número racional. | ||
| Línea 237: | Línea 237: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=2. Coloca junto a cada fracción su fracción irreducible. | + | |enunciado='''Actividad 2:''' Coloca junto a cada fracción su fracción irreducible. |
| |actividad={{p}} | |actividad={{p}} | ||
| * '''Nivel 1:''' | * '''Nivel 1:''' | ||
| Línea 298: | Línea 298: | ||
| {{AI2|titulo=Actividad Interactiva: ''Ordenar fracciones''|cuerpo= | {{AI2|titulo=Actividad Interactiva: ''Ordenar fracciones''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=1. Ordena de menor a mayor estas fracciones. | + | |enunciado='''Actividad 1:''' Ordena de menor a mayor estas fracciones. |
| |actividad= | |actividad= | ||
| Coloca estas fracciones ordenadas de menor a mayor. | Coloca estas fracciones ordenadas de menor a mayor. | ||
| Línea 336: | Línea 336: | ||
| {{AI2|titulo=Actividad Interactiva: ''''Suma y resta de fracciones''|cuerpo= | {{AI2|titulo=Actividad Interactiva: ''''Suma y resta de fracciones''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=1. Aprende a sumar y restar fracciones. | + | |enunciado='''Actividad 1:''' Aprende a sumar y restar fracciones. |
| |actividad= | |actividad= | ||
| Cuando tenemos juntas sumas y restas seguimos el mismo proceso que si tuviéramos solamente sumas. | Cuando tenemos juntas sumas y restas seguimos el mismo proceso que si tuviéramos solamente sumas. | ||
| Línea 358: | Línea 358: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=2. Halla el resultado de estas sumas y restas de fracciones. | + | |enunciado='''Actividad 2:''' Halla el resultado de estas sumas y restas de fracciones. |
| |actividad= | |actividad= | ||
| Realiza en papel aparte estas operaciones y luego marca aquí su resultado. | Realiza en papel aparte estas operaciones y luego marca aquí su resultado. | ||
| Línea 393: | Línea 393: | ||
| {{AI2|titulo=Actividad Interactiva: ''''Producto de fracciones''|cuerpo= | {{AI2|titulo=Actividad Interactiva: ''''Producto de fracciones''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=1. Aprende a multiplicar fracciones. | + | |enunciado='''Actividad 1:''' Aprende a multiplicar fracciones. |
| |actividad= | |actividad= | ||
| Para multiplicar fracciones no hace falta pasarlas a común denominador, se multiplican directamente. | Para multiplicar fracciones no hace falta pasarlas a común denominador, se multiplican directamente. | ||
| Línea 412: | Línea 412: | ||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=2. Halla el resultado de estas multiplicaciones de fracciones. | + | |enunciado='''Actividad 2:''' Halla el resultado de estas multiplicaciones de fracciones. |
| |actividad= | |actividad= | ||
| Realiza en papel aparte estas operaciones y luego marca aquí su resultado. | Realiza en papel aparte estas operaciones y luego marca aquí su resultado. | ||
| Línea 438: | Línea 438: | ||
| {{AI2|titulo=Actividad Interactiva: ''Inversa de una fracción''|cuerpo= | {{AI2|titulo=Actividad Interactiva: ''Inversa de una fracción''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=1. Halla la fracción inversa de una fracción. | + | |enunciado='''Actividad 1:''' Halla la fracción inversa de una fracción. |
| |actividad= | |actividad= | ||
| La inversa de una fracción es otra fracción que al ser multiplicada por ella da la fracción unidad. | La inversa de una fracción es otra fracción que al ser multiplicada por ella da la fracción unidad. | ||
| Línea 477: | Línea 477: | ||
| {{AI2|titulo=Actividad Interactiva: ''Cociente de fracciones''|cuerpo= | {{AI2|titulo=Actividad Interactiva: ''Cociente de fracciones''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=1. Aprende a dividir fracciones. | + | |enunciado='''Actividad 1:''' Aprende a dividir fracciones. |
| |actividad= | |actividad= | ||
| Dividir una fracción por otra es lo mismo que multiplicar la primera fracción por la inversa de la segunda fracción. Una fracción se puede dividir por cualquier otra, menos por la fracción 0. | Dividir una fracción por otra es lo mismo que multiplicar la primera fracción por la inversa de la segunda fracción. Una fracción se puede dividir por cualquier otra, menos por la fracción 0. | ||
Revisión de 18:35 25 jun 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones I Fracciones II Fracciones III Números decimales | WIRIS Geogebra Calculadora Fracciones |
Tabla de contenidos |
Definiciones
Fracciones o números racionales
Así como los números naturales surgen para expresar cantidades que se refieren a objetos enteros, las fracciones son consecuencia de expresar cantidades que se refieren a partes de un objeto. Una fracción se expresa de la forma con
con 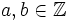 , donde
, donde  se llama numerador y
se llama numerador y  denominador. El denominador indica las partes iguales en que se divide a la unidad y el numerador las partes que tomamos.
denominador. El denominador indica las partes iguales en que se divide a la unidad y el numerador las partes que tomamos.
El valor de una fracción es el resultado de dividir numerador entre denominador.
Al conjunto de todas las fracciones también se le llama conjunto de números racionales. Lo representaremos por 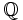 .
.
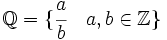
Si el numerador es divisible por el denominador, la fracción representa a un número entero. Así, los racionales contienen a los enteros y éstos a los naturales.
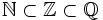 |
|
Actividades Interactivas: Fracciones
Actividad 1: Concepto de fracción.
Actividad:
Actividad 2: ¿Qué fracción representa cada figura?
Actividad:
Actividad 3: Representación de las fracciones en la recta numérica.
Actividad:
Actividad 4: Adivina la posición de cada fracción en la recta numérica.
Actividad: |
Fracciones propias e impropias
Fracciones propias son aquellas cuyo numerador es menor que el denominador. Son menores que 1.
Fracciones impropias son aquellas cuyo numerador es mayor o igual que el denominador. Son mayores que 1.
|
Actividades Interactivas: Fracciones propias e impropias
Actividad 1: Definición de fracción propia e impropia.
Actividad:
Actividad 2: Separa las fracciones propias de las impropias.
Actividad: Puesto que una fracción representa una división, para saber cuál es el valor de una fracción deberíamos realizar esa división, no obstante, podemos apreciar el valor de una fracción si nos fijamos en su numerador y su denominador. Su valor será más grande cuanto mayor tenga el numerador, y será más pequeño cuanto mayor tenga el denominador.
Coloca cada fracción en el rectángulo que le corresponda según su valor. Pulsa "inicio" para que aparezcan otras fracciones. |
Fracciones equivalentes
Fracciones equivalentes son aquellas que, aún teniendo distinto numerador y denominador, tienen el mismo valor.
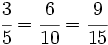
Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden.
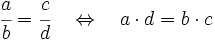
|
Actividades Interactivas: Fracciones equivalentes
Actividad 1: Definición de fracciones equivalentes.
Actividad:
Actividad 2: Busca una fracción equivalente a la dada.
Actividad: En la siguiente escena, escribe el numerador y denominador de otra fracción equivalente a ella y pulsa "intro" o usa los pulsadores. Pulsa "inicio" para que aparezca otra fracción.
Actividad 3: Comprueba si dos fracciones son equivalentes o no (Método de los productos cruzados).
Actividad: Para comprobar si dos fracciones son equivalentes o no, el método más fácil es el de los productos cruzados. Multiplicamos sus términos en aspa. El producto del numerador de una fracción por el denominador de la otra ha de dar lo mismo en ambos casos. En la siguiente escena, escribe el numerador y denominador de otra fracción equivalente a ella y pulsa "intro" o usa los pulsadores. Después, pulsa sobre el triángulo azul para ver paso a paso la comprobación. Pulsa "inicio" para que aparezca otra fracción.
Actividad 4: Junta las fracciones equivalentes.
Actividad: Cada fracción de abajo es equivalente a otra de arriba. Colócala junto a ella. Para ello puedes buscar la fracción irreducible de cada una, o comprobar los productos cruzados de ambas. Pulsa "inicio" para que aparezcan otras fracciones.
Actividad 5: Agrupa las fracciones equivalentes.
Actividad: |
Simplificar fracciones. Fracciones irreducibles
Simplificar una fracción consiste en obtener otra fracción equivalente con numerador y denominador menores. Para ello debemos dividir numerador y denominador por un mismo número. Este proceso se puede repetir hasta que ya no encontremos más divisores comunes distintos de 1, en cuyo caso, la fracción obtenida se dice que es irreducible.
|
Actividades Interactivas: Simplificación de fracciones
Actividad 1: Simplifica las fracciones.
Actividad: Todas las fracciones equivalentes entre sí representan el mismo número racional. Por tanto, para expresar un mismo valor nos interesa emplear la fracción más simple, ésa será la que tenga el numerador y denominador más pequeños. A esa fracción se la llama fracción irreducible porque ya no se la puede simplificar más. Nos valemos de la propiedad fundamental de la división. Sabemos que si multiplicamos o dividimos al numerador y al denominador por el mismo número obtenemos otra fracción equivalente. Para simplificar una fracción debemos buscar un número que sea divisor del numerador y del denominador para dividirlos por él. Nos interesa dividirlos por el número mayor posible, ese número es el máximo común divisor de ambos, así, de una sola vez habremos llegado a la fracción irreducible.
En esta escena aparece aleatoriamente una fracción, además se indican los divisores comunes del numerador y del denominador. Abajo debes marcar el número por el que dividirías al numerador y denominador para simplificar esa fracción. Pulsa "inicio" para que aparezca otra fracción.
Esta actividad es semejante a la anterior, pero en ésta no se da ayuda. Busca un número por el que puedes simplificar esta fracción, márcalo abajo y pulsa intro. Te indicará si con ello has llagado a la fracción irreducible o si todavía puedes seguir simplificando. En ese caso marca otro número. Tienes tres intentos para llegar a la fracción irreducible, pero no puedes rectificar, por eso no utilices los triángulos para cambiar los números marcados. Si la primera fracción es ya irreducible, marca el 1. Pulsa "inicio" para que aparezca otra fracción.
Actividad 2: Coloca junto a cada fracción su fracción irreducible.
Actividad:
Las fracciones de abajo son las irreducibles de las fracciones de arriba. Colócalas juntas. Pulsa "inicio" para que aparezcan otras fracciones.
Esta actividad es semejante a la anterior, empleando números de hasta dos cifras. Pulsa "inicio" para que aparezcan otras fracciones.
Esta actividad es semejante a la anterior, empleando números de hasta tres cifras. Pulsa "inicio" para que aparezcan otras fracciones. |
Orden
De dos fracciones con el mismo denominador, es mayor la de mayor numerador. Por eso, para ordenar fracciones, debemos primero obtener fracciones equivalentes a las dadas, pero con el mismo denominador. A ésto se le llama reducir a común denominador. Veamos un ejemplo:
Ejemplo: Ordenar fracciones
- Ordena las fracciones:
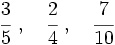
Primero reducimos a común denominador. Para ello, calculamos el m.c.m. de los denominadores:
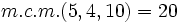 .
.Obtenemos fracciones equivalentes a las dadas con denominador 20. Para ello dividimos 20 entre cada denominador y lo multiplicamos por el numerador. Las fracciones obtenidas son:
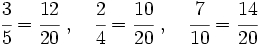
Estas fracciones las podemos ordenar fácilmente porque tienen el mismo denominador:
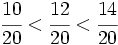
Así obtenemos:
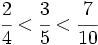
|
Actividad Interactiva: Ordenar fracciones
Actividad 1: Ordena de menor a mayor estas fracciones.
Actividad: Coloca estas fracciones ordenadas de menor a mayor. Pulsa "inicio" para que aparezcan otras fracciones. |
Operaciones con fracciones
Suma y resta
Para sumar o restar fracciones:
- Si las fracciones tienen el mismo denominador, se suman o restan los numeradores y se pone el mismo denominador.
- Si tienen distintos denominadores, primero se reducen a común denominador y luego se procede como en el caso anterior.
Ejemplo: Suma y resta de fracciones
- Calcula:
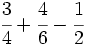
Primero reducimos a común denominador. Para ello, calculamos el m.c.m. de los denominadores:
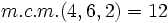 .
.
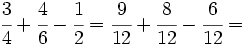
Luego sumamos o restamos los númeradores, dejando el mismo denominador:
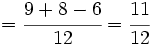
|
Actividad Interactiva: ''Suma y resta de fracciones
Actividad 1: Aprende a sumar y restar fracciones.
Actividad: Cuando tenemos juntas sumas y restas seguimos el mismo proceso que si tuviéramos solamente sumas. Para sumar y restar fracciones es necesario que tengan todas el mismo denominador. Si las fracciones tienen distintos denominadores se pasan a común denominador, es decir, se cambian por otras equivalentes a ellas pero con el mismo denominador todas. Para ello se siguen estos pasos:
En esta escena puedes ver el proceso paso a paso, pulsando sobre el triángulo azul. Pulsa "inicio" para que aparezcan otras fracciones.
Actividad 2: Halla el resultado de estas sumas y restas de fracciones.
Actividad: Realiza en papel aparte estas operaciones y luego marca aquí su resultado. Marca primero su numerador, pulsa intro, luego marca su denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no permite rectificaciones, por eso no emplees los triángulos para variar el número marcado. Pulsa "inicio" para que aparezcan otras fracciones. |
Multiplicación
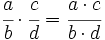
Ejemplo: Producto de fracciones
- Calcula:
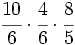
Multiplicamos numeradores y denominadores, simplificando antes de efectuar el producto:
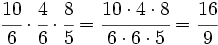
|
Actividad Interactiva: ''Producto de fracciones
Actividad 1: Aprende a multiplicar fracciones.
Actividad: Para multiplicar fracciones no hace falta pasarlas a común denominador, se multiplican directamente. Multiplicamos sus numeradores y lo ponemos de numerador, multiplicamos sus denominadores y lo ponemos de denominador. A continuación se simplifican. No obstante, es conveniente simplificar antes de multiplicar. En esta escena puedes ver el proceso paso a paso, pulsando sobre el triángulo azul. Pulsa "inicio" para que aparezcan otras fracciones.
Actividad 2: Halla el resultado de estas multiplicaciones de fracciones.
Actividad: Realiza en papel aparte estas operaciones y luego marca aquí su resultado. Marca primero su numerador, pulsa intro, luego marca su denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no permite rectificaciones, por eso no emplees los triángulos para variar el número marcado. Pulsa "inicio" para que aparezcan otras fracciones. |
Inversa
Dada una fracción 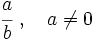 , su inversa es la fracción
, su inversa es la fracción 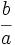 .
.
Por ejemplo, la inversa de 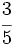 es
es 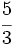 .
.
|
Actividad Interactiva: Inversa de una fracción
Actividad 1: Halla la fracción inversa de una fracción.
Actividad: La inversa de una fracción es otra fracción que al ser multiplicada por ella da la fracción unidad. La fracción que tiene el numerador y denominador intercambiados respecto de ella, es su fracción inversa. Lógicamente, si una fracción es inversa de otra, también son sus inversas todas las equivalentes a esa. La fracción de valor 0 es la única que no tiene inversa. Marca la fracción inversa, para ello debes marcar primero el numerador, pulsar intro, después el denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no admite rectificaciones, por eso no puedes utilizar los triángulos para variar los números marcados. Pulsa "inicio" para que aparezca otra fracción. |
División
Para dividir dos fracciones, se pone como numerador, el producro del primer numerador por el segundo denominador, y como denominador, el producto del primer denominador por el segundo numerador.
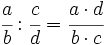
Ejemplo: Cociente de fracciones
- Calcula:
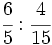
Multiplicamos en cruz, simplificando antes de efectuar el producto:
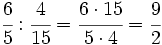
|
Actividad Interactiva: Cociente de fracciones
Actividad 1: Aprende a dividir fracciones.
Actividad: Dividir una fracción por otra es lo mismo que multiplicar la primera fracción por la inversa de la segunda fracción. Una fracción se puede dividir por cualquier otra, menos por la fracción 0. Haz la división en tu cuaderno y luego comprueba el resultado, viendo el desarrollo paso a paso. Para ello pulsa la flecha azul. Pulsa "inicio" para que aparezca otra fracción. |
Potenciación
Las potencias con números racionales cumplen las mismas propiedades que con números naturales y enteros. Tan sólo mencionar el siguiente caso:
Potencias de exponente negativo
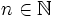 , se define:
, se define: 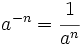
Como consecuencia, 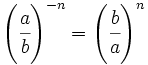 .
.
Expresión decimal de una fracción
Paso de fracción a decimal
Para pasar de fracción a decimal basta con hacer la división del numerador entre el denominador. Pueden darse los siguientes casos, según sea la expresión decimal resultante:- Expresión decimal exacta: Si tiene un número finito de decimales.
- Por ejemplo:
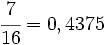 .
.
- Expresión decimal periódica pura: Si tiene un número infinito de decimales que se repiten. La parte que se repite se llama periodo.
- Por ejemplo:
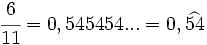 . El periodo es 54.
. El periodo es 54.
- Expresión decimal periódica mixta: Si tiene un número infinito de decimales que se repiten a partir de una cierta posición decimal. La parte que se repite se llama periodo y la parte decimal previa al periodo se llama anteperiodo.
- Por ejemplo:
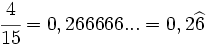 . El periodo es 6 y el anteperiodo 2.
. El periodo es 6 y el anteperiodo 2.
Identificar el tipo de expresión decimal sin hacer la división
Se puede saber, sin hacer la división, que tipo de expresión decimal tiene una fracción. Para ello, deberemos simplificar la fracción y nos fijaremos en la descomposición del denominador en factores primos. Tendremos los siguientes casos:
- Si el denominador sólo contiene factores que sean 2 ó 5, la fracción tiene una expresión decimal exacta.
- Si el denominador no contiene factores que sean 2 ó 5, la fracción tiene una expresión decimal periódica pura.
- Si el denominador contiene mezcla de factores que sean 2 ó 5, con otros distintos de 2 ó 5, la fracción tiene una expresión decimal periódica mixta.
Paso de decimal a fracción
Recíprocamente, todo número con un desarrollo decimal puede expresarse en fracción de la siguiente manera:
- Decimales exactos: Se escribe en el numerador la expresión decimal sin la coma, y en el denominador un uno seguido de tantos ceros como cifras decimales.
- Ejemplo:
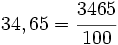
- Decimales periódicos puros: La fracción de un número decimal periódico tiene como numerador la diferencia entre el número escrito sin la coma y la parte anterior al periodo; y como denominador, tantos "9" como cifras tiene el periodo.
- Ejemplo:
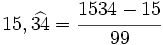
- Decimales periódicos mixtos: Tendrá como numerador la diferencia entre a y b, donde a es el número escrito sin la coma, y b es el número sin la parte decimal periódica, escrito como número entero. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras tenga el anteperiodo.
- Ejemplo: Sea el número
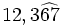 entonces a=12367 y b=123, por lo que el número buscado será:
entonces a=12367 y b=123, por lo que el número buscado será:
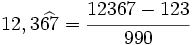
Veamos unos ejemplos que ilustren el porqué de tales procedimientos:
Ejemplo: Paso de decimal a fracción
- Expresa en forma de fracción los números decimales:
- a)
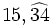 b)
b) 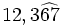
- a)
- a)
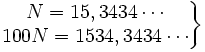 Restando:
Restando: 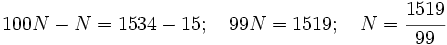
- b)
 Restando:
Restando: 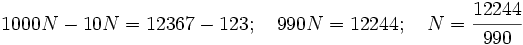
Ejercicios y problemas
Ejercicios
|
Ejercicios: 1. Agrupa las fracciones que sean equivalentes: Solución: 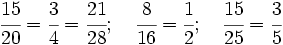 2. Simplifica las fracciones:
Solución: a) 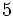 b) b) 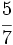 c) c) 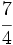 3. Ordena de menor a mayor las fracciones: Solución: 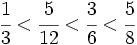 4. Opera las fracciones:
Solución: a) 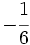 b) b) 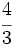 c) c) 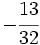 5. Simplifica y expresa en forma de fracción:
Solución: a) 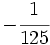 b) b) 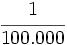 c) c) 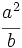 6. Simplifica:
Solución: a) 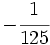 b) b) 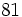 c) c) 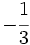 7. Sin hacer la división, indica qué tipo de decimal resulta:
Solución: a) Decimal exacto; b) Decimal periódico puro; c) Decimal periódico mixto. 8. Expresa en forma de fracción:
Solución: a) 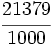 b) b) 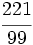 c) c) 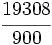 |
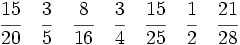
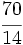 b)
b)  c)
c) 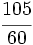
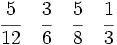
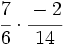 b)
b) 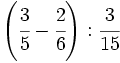 c)
c) 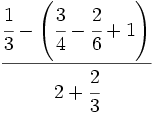
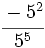 b)
b) 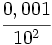 c)
c) 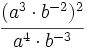
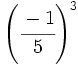 b)
b) ![\left [ \left ( \cfrac{-1}{3} \right )^{-2} \right ]^2](/wikipedia/images/math/1/4/e/14e6c8e9222f905775e21fb947d71f2c.png) c)
c) 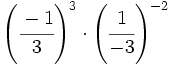
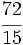 b)
b) 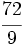 c)
c)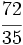
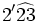 c)
c)