Sucesiones
De Wikipedia
| Revisión de 18:30 18 sep 2007 Juanmf (Discusión | contribuciones) (→Progresiones aritméticas) ← Ir a diferencia anterior |
Revisión de 17:15 3 oct 2007 Coordinador (Discusión | contribuciones) (→Definiciones) Ir a siguiente diferencia → |
||
| Línea 13: | Línea 13: | ||
| Se nombran con una letra y un subíndice que depende del lugar que el término ocupa en la sucesión. | Se nombran con una letra y un subíndice que depende del lugar que el término ocupa en la sucesión. | ||
| <center> | <center> | ||
| - | <math>a_1,a_2,a_3,a_4,...</math></center> | + | <math>a_1,a_2,a_3,a_4, \cdots \;\!</math></center> |
| - | Según lo dicho, <math>a_{10}</math> designará al término que ocupa el décimo lugar dentro de una sucesión, en el ejemplo es el 20. | + | Según lo dicho, <math>a_{10}\;\!</math> designará al término que ocupa el décimo lugar dentro de una sucesión, en el ejemplo es el 20. |
| - | A veces, podemos encontrar una expresión (fórmula) que sirve para obtener un término cualquiera de la sucesión con solo saber el lugar que este ocupa. A esta expresión se le llama '''término general'''. El término general de la sucesión del ejemplo es <math>a_n=2n</math> | + | A veces, podemos encontrar una expresión (fórmula) que sirve para obtener un término cualquiera de la sucesión con solo saber el lugar que este ocupa. A esta expresión se le llama '''término general'''. El término general de la sucesión del ejemplo es <math>a_n=2n\;\!</math> |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 17:15 3 oct 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Definiciones
Sucesión de números: Conjunto de infinitos números ordenados. Ejemplo: 2,4,6,8,10,......
Término de una sucesión: Cada uno de los números que la componen. Se nombran con una letra y un subíndice que depende del lugar que el término ocupa en la sucesión.
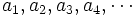
Según lo dicho, 
designará al término que ocupa el décimo lugar dentro de una sucesión, en el ejemplo es el 20.
A veces, podemos encontrar una expresión (fórmula) que sirve para obtener un término cualquiera de la sucesión con solo saber el lugar que este ocupa. A esta expresión se le llama término general. El término general de la sucesión del ejemplo es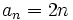 
 Problemas 1. Intenta escribir una expresión que sirva para calcular cualquier término de las sucesiones siguientes: a) 1,2,3,4,5,..... b) 1,4,9,16,..... c) 1,3,5,7,..... d) 1/2,1/4,1/8,... e) -1,1,-1,1,-1,.. f) 1,-1,1,-1,1,.....Solución: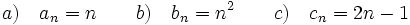 
 |
