Sistemas de ecuaciones de primer grado
De Wikipedia
| Revisión de 18:41 9 oct 2007 Coordinador (Discusión | contribuciones) (→Número de soluciones de un sistema) ← Ir a diferencia anterior |
Revisión de 18:51 9 oct 2007 Coordinador (Discusión | contribuciones) (→Número de soluciones de un sistema) Ir a siguiente diferencia → |
||
| Línea 77: | Línea 77: | ||
| |titulo=''Número de soluciones de un sistema 2x2'' | |titulo=''Número de soluciones de un sistema 2x2'' | ||
| |enunciado=Un sistema 2x2 puede ser: | |enunciado=Un sistema 2x2 puede ser: | ||
| - | *Compatible determinado (S.C.D.) | + | *Compatible determinado (S.C.D.): 1 solución |
| - | *Compatible indeterminado (S.C.I.) | + | *Compatible indeterminado (S.C.I.): Infinitas soluciones. |
| - | *Incompatible (S.I) | + | *Incompatible (S.I): 0 soluciones. |
| |demo= | |demo= | ||
| En efecto, razonando a partir de sus representaciones gráficas: | En efecto, razonando a partir de sus representaciones gráficas: | ||
Revisión de 18:51 9 oct 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Sistemas de ecuaciones 2x2
- Un sistema de dos ecuaciones de primer grado con dos incógnitas o simplemente, sistema 2x2, es
la agrupación de dos ecuaciones de primer grado con dos incógnitas:
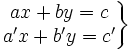
- Se llama solución de un sistema 2x2 a cualquier pareja de valores de x e y que sean solución de ambas ecuaciones a la vez. Las soluciones de un sistema son los puntos de corte de las rectas que representan cada una de las ecuaciones del sistema.
Ejemplo: Solución de un sistema de ecuaciones
- Comprueba si las parejas de números
; 
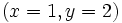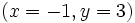son o no soluciones del sistema:
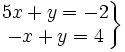
- Sustituimos los valores 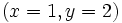en las dos ecuaciones del sistema:
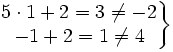
Como no se verifican las dos ecuaciones, la pareja 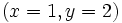no es solución del sistema.
- Sustituimos los valores 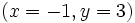en las dos ecuaciones del sistema:
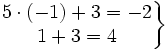
Ahora si se verifican las dos ecuaciones, por tanto, la pareja 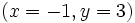si es solución del sistema.
Comprueba en la siguiente escena la solución del sistema. para ello deberás introducir los coeficientes de cada ecuación en las casillas correspondientes.
Sistemas equivalentes
Dos sistemas son equivalentes cuando tienen las mismas soluciones.
 Actividad Interactiva: Sistemas equivalentes
Actividad 1: Obteniendo sistemas equivalentes. Comprobación gráfica.
Actividad: Dado el siguiente sistema 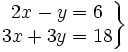 a) Represéntalo gráficamente. b) Multiplica la primera ecuación por 3 y divide la segunda por 3. Representa el nuevo sistema. c) Resta a la 2ª ecuación la 1ª ecuación y representa sobre la gráfica anterior la nueva ecuación. d) Suma a la 1ª ecuación la 2ª multiplicada por 5 y representa la nueva ecuación en la gráfica anterior. e) Comprueba el proceso en la siguiente escena: |
Número de soluciones de un sistema
- Un sistema es compatible si tiene solución e incompatible si no la tiene.
- Un sistema es determinado si tiene una única solución e indeterminado si tiene infinitas soluciones.
Número de soluciones de un sistema 2x2
Un sistema 2x2 puede ser:
- Compatible determinado (S.C.D.): 1 solución
- Compatible indeterminado (S.C.I.): Infinitas soluciones.
- Incompatible (S.I): 0 soluciones.
En efecto, razonando a partir de sus representaciones gráficas:
- Si las dos rectas se cortan en un punto: 1 solución (S.C.D.)
- Si las dos rectas son coincidentes: Infinitas soluciones (S.C.I.)
- Si las rectas son paralelas: 0 soluciones (S.I.)
}}
Actividad Interactiva: Soluciones de un sistema
Actividad 1: Sistema incompatible.
Actividad: Dado el siguiente sistema 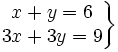 a) Represéntalo gráficamente b) ¿Cómo son las rectas que aparecen? c) ¿Existe algún punto que pertenezca a ambas rectas? d) ¿Cuantas soluciones tiene el sistema? e) Utiliza la escena para comprobar los resultados:
Actividad 2: Sistema compatible indeterminado.
Actividad: Dado el siguiente sistema 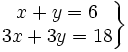 a) Represéntalo gráficamente b) ¿Cómo son las rectas que aparecen? c) ¿Existe algún punto que pertenezca a ambas rectas? d) ¿Cuantas soluciones tiene el sistema? e) Utiliza la escena para comprobar los resultados:
Actividad 3: Sistema compatible determinado.
Actividad: Dado el siguiente sistema 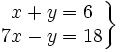 a) Represéntalo gráficamente b) ¿Cómo son las rectas que aparecen? c) ¿Existe algún punto que pertenezca a ambas rectas? d) ¿Cuantas soluciones tiene el sistema? e) Utiliza la escena para comprobar los resultados: |
