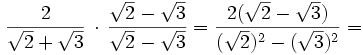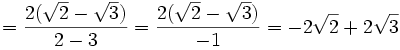Radicales (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
(pág. 34)
Raíz n-ésima de un número
La raíz n-ésima  de un número
de un número  es otro número
es otro número  tal que
tal que 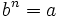 y que escribimos simbólicamente
y que escribimos simbólicamente ![b=\sqrt[n]{a}](/wikipedia/images/math/c/e/0/ce05f9d287d25fe0a5fd8e680bd177f5.png) .
.
![\sqrt[n]{a}=b \iff b^n =a](/wikipedia/images/math/f/f/7/ff79017c635440f207b67b250c3660fb.png)
El número  se llama radicando, el número
se llama radicando, el número  índice y
índice y  la raíz.
la raíz.
Si el índice es 2 las llamaremos raíces cuadradas; si el índice es 3, raíces cúbicas; si es 5, 6, ..., raíces cuartas, quintas, ....
Propiedades de las raíces
Propiedades
![\sqrt[n]{1}=1](/wikipedia/images/math/f/2/3/f2301fcbef74b110ad8d373f2b32a16b.png) ;
; ![\sqrt[n]{0}=0](/wikipedia/images/math/8/6/5/865db751c6cb2e12533fccdf8de1e1df.png) , para cualquier valor del índice
, para cualquier valor del índice  .
.
- Si
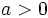 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) existe cualquiera que sea el índice
existe cualquiera que sea el índice  .
.
- Si
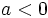 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) sólo existe si el índice
sólo existe si el índice  es impar.
es impar.
- Si el índice
 es par y el radicando
es par y el radicando 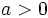 , la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto.
, la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto.
- Si el índice
 es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando
es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando  .
.
Tutorial que explica la definición de raíz (radical) realizando el cálculo de alguna raíces exactas de números racionales (enteros y decimales).
Raíz n-ésmina de un número. Ejemplos sencillos.
Raíz n-ésmina de un número. Ejemplos más complejos.
Raíz n-ésmina de un número. Ejemplos sencillos.
- Raíces de un número entero.
- Raíces cuadradas y cúbicas.
- Partes de una raíz.
- Raíces de números positivo, negativos y del cero.
- Raíz exacta y raíz entera.
- Calculo manual de raíces cuadradas.
- Los radicales.
- Extracción de factores de un radical.
1) Completa:
- 1a)
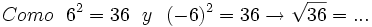
- 1b)
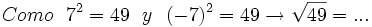
- 1c)
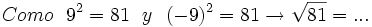
- 1d)
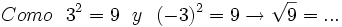
2) Completa:
- 2a)
![Como \ \ 6^3=216 \rightarrow \sqrt[3]{216}= ...](/wikipedia/images/math/3/c/3/3c378630d2615778e963ac624db86d87.png)
- 2b)
![Como \ \ (-6)^3=-216 \rightarrow \sqrt[3]{-216}= ...](/wikipedia/images/math/6/5/8/6587736293705d54e8f32954028d084c.png)
- 2c)
![Como \ \ 5^3=125 \rightarrow \sqrt[3]{125}= ...](/wikipedia/images/math/b/d/b/bdb68c764c3249b6a9780aa720742319.png)
- 2d)
![Como \ \ (-5)^3=-125 \rightarrow \sqrt[3]{-125}= ...](/wikipedia/images/math/e/7/0/e705216d0789f62aef7ec241081fabeb.png)
- 2e)
![Como \ \ 7^3=343 \rightarrow \sqrt[3]{343}= ...](/wikipedia/images/math/5/f/2/5f298eabe3ed377592f625e71f6488c0.png)
- 2f)
![Como \ \ (-7)^3=-343 \rightarrow \sqrt[3]{-343}= ...](/wikipedia/images/math/c/e/5/ce577674faca3babb2d3dfaac0413e21.png)
3) Completa:
- 3a)
![Como \ \ 6^4=216 \ \ y \ \ (-6)^4 =216 \rightarrow \sqrt[4]{216}= ...](/wikipedia/images/math/c/b/4/cb4b33e4c8e211ead755140a2c66bba9.png)
- 3b)
![Como \ \ 2^5=32 \ \ y \ \ (-2)^5 =32 \rightarrow \sqrt[5]{32}= ... \ \ y \ \ \sqrt[5]{-32}= ...](/wikipedia/images/math/c/c/c/ccc2a79c409e95a6ea8eb4d3dd464bae.png)
- 3c)
![Como \ \ 3^6=729 \ \ y \ \ (-3)^6 =729 \rightarrow \sqrt[6]{729}= ...](/wikipedia/images/math/b/5/5/b554d8cc9395627f020eb1f365124e4e.png)
- 3d)
![Como \ \ 2^7=128 \ \ y \ \ (-2)^7 =-128 \rightarrow \sqrt[7]{128}= ... \ \ y \ \ \sqrt[7]{-128}= ...](/wikipedia/images/math/a/d/6/ad64ef0e208078f3159cae14f80cd300.png)
- 3e)
![Como \ \ 3^8=6561 \ \ y \ \ (-3)^8 =6561 \rightarrow \sqrt[8]{6561}= ...](/wikipedia/images/math/7/b/a/7ba166f1a52a30e3ea2be20046fc6f29.png)
- 3f)
![Como \ \ 2^9=512 \ \ y \ \ (-2)^9 =-512 \rightarrow \sqrt[9]{512}= ... \ \ y \ \ \sqrt[9]{-512}= ...](/wikipedia/images/math/3/a/9/3a962574019bdc46ed38d924b83f207c.png)
- 3g)
![Como \ \ 2^{10}=1024 \ \ y \ \ (-2)^{10} =1024 \rightarrow \sqrt[10]{1024}= ...](/wikipedia/images/math/7/e/d/7edae10fccfe7b465c672d8c9c045b91.png)
4) Contesta:
- 4a) ¿Hay algún número que elevado al cuadrado dé -25? ¿Existe
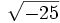 ?
?
- 4b) ¿Hay algún número que elevado al cuadrado dé -36? ¿Existe
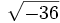 ?
?
- 4c) ¿hay algún número que elevado al cuadrado dé un número negativo?
- 4d) ¿Hay algún número que elevado al cubo dé -27? ¿Existe
![\sqrt[3]{-27}\;](/wikipedia/images/math/7/f/9/7f964050f55904a351871c909842d531.png) ?
?
- 4e) ¿Hay algún número que elevado al cubo dé -64? ¿Existe
![\sqrt[3]{-64}\;](/wikipedia/images/math/1/a/c/1ac847b9288b852f7e2cd46adb661650.png) ?
?
- 4f) ¿hay algún número que elevado al cubo dé un número negativo?
- 4g) ¿Hay algún número que elevado a la cuarta dé -81? ¿Existe
![\sqrt[4]{-81}\;](/wikipedia/images/math/9/3/8/9380cfbe25a5f6b1f53b0e98557d5cb3.png) ?
?
- 4h) ¿Hay algún número que elevado a la quinta dé -243? ¿Existe
![\sqrt[5]{-243}\;](/wikipedia/images/math/0/0/d/00d129c231e444389e6e90b5a1a8e808.png) ?
?
- 4i) ¿De qué depende que exista una raíz de radicando negativo?
5) Calcula:
- 5a)
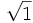 ;
; 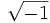
- 5b)
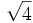 ;
; 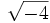
- 5c)
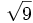 ;
; 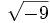
- 5d)
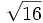 ;
; 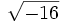
- 5e)
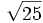 ;
; 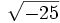
- 5f)
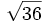 ;
; 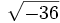
- 5g)
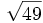 ;
; 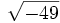
- 5h)
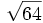 ;
; 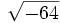
- 5i)
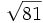 ;
; 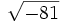
- 5j)
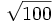 ;
; 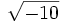
6) Calcula:
- 6a)
![\sqrt[3]{1}\;](/wikipedia/images/math/a/9/e/a9ed184fd0349444d061cc1d272e67c6.png) ;
; ![\sqrt[3]{-1}\;](/wikipedia/images/math/9/1/7/917ae3af6a2d50278779cc91cbbdea73.png)
- 6b)
![\sqrt[3]{8}\;](/wikipedia/images/math/1/3/2/132c2f74c8498afa99586eeab29a92a8.png) ;
; ![\sqrt[3]{-8}\;](/wikipedia/images/math/2/2/3/2232a48fe703bd572c3668d1f57c0066.png)
- 6c)
![\sqrt[3]{27}\;](/wikipedia/images/math/f/f/d/ffdb842d7cefcf30ac4e11b74ccdc8f3.png) ;
; ![\sqrt[3]{-27}\;](/wikipedia/images/math/7/f/9/7f964050f55904a351871c909842d531.png)
- 6d)
![\sqrt[3]{64}\;](/wikipedia/images/math/4/b/d/4bd0c615f84c6543e9f004c6bcfce737.png) ;
; ![\sqrt[3]{-64}\;](/wikipedia/images/math/1/a/c/1ac847b9288b852f7e2cd46adb661650.png)
- 6e)
![\sqrt[3]{125}\;](/wikipedia/images/math/9/b/0/9b0b656102d06b662a6c1cfa6f46ee4c.png) ;
; ![\sqrt[3]{-125}\;](/wikipedia/images/math/b/d/6/bd68acb8f905cf5984575d47adbbe028.png)
6) Calcula:
- 7a)
![\sqrt[4]{1}\;](/wikipedia/images/math/4/2/3/42348ffb6e4d069c36b7529b4c3d61c7.png) ;
; ![\sqrt[4]{-1}\;](/wikipedia/images/math/3/0/4/3041c7b2e1985e0ce2b4e12419b1adfd.png)
- 7b)
![\sqrt[5]{32}\;](/wikipedia/images/math/5/a/4/5a4316aef4d84ea09023226c0b455ef1.png) ;
; ![\sqrt[5]{-32}\;](/wikipedia/images/math/e/4/b/e4b2e7ef8b833cd852ca9c1bedfade9b.png)
- 7c)
![\sqrt[6]{729}\;](/wikipedia/images/math/6/4/5/645cad2d63e42973a6e2a66d954d5272.png) ;
; ![\sqrt[6]{-729}\;](/wikipedia/images/math/c/8/9/c89f55205c50d79be31feca9e8e7fe21.png)
- 7d)
![\sqrt[7]{128}\;](/wikipedia/images/math/e/4/e/e4e24abf54c49df327ec72213ca1b2bd.png) ;
; ![\sqrt[7]{-128}\;](/wikipedia/images/math/5/7/f/57ff532d80dc61569bbab4448a648df4.png)
8) Indica, en cada caso, la raíz, el índice y el radicando:
- 8a)
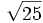
- 8b)
![\sqrt[3]{-64}\;](/wikipedia/images/math/1/a/c/1ac847b9288b852f7e2cd46adb661650.png)
- 8c)
![\sqrt[4]{81}\;](/wikipedia/images/math/0/4/d/04d103e445158aa43cb56526c68b98c2.png)
9) Completa:
- 9a)
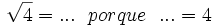
- 9b)
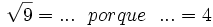
- 9c)
![\sqrt[3]{-8}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/b/b/c/bbc65bbad66511345d7cb3ac4f7a001c.png)
- 9d)
![\sqrt[3]{8}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/3/e/c/3ec4111d51daf4478bc80d3d1bd1ef0a.png)
- 9e)
![\sqrt[4]{16}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/2/0/8/208788fa3a4920a05007fa9edad8dbc6.png)
- 9f)
![\sqrt[5]{32}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/f/5/5/f552d101987249877deb51a2875a57db.png)
- 9g)
![\sqrt[5]{-32}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/a/b/9/ab988d19836d333dfc399b9f3fefee8c.png)
- 9f)
![\sqrt[6]{1}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/7/0/6/70646a208681230895b71a7e18b7317b.png)
10) Calcula las raíces enteras por exceso y por defecto:
- 10a)
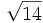 ;
; ![\sqrt[3]{14}\;](/wikipedia/images/math/4/d/9/4d90b08a8a7ba14e1c60f25be0fb24ef.png)
- 10b)
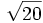 ;
; ![\sqrt[3]{20}\;](/wikipedia/images/math/f/a/a/faaf025a7b9f3b036eb836c60d8e4e34.png)
- 10c)
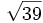 ;
; ![\sqrt[3]{39}\;](/wikipedia/images/math/c/9/f/c9f16a3fa799c3b21b4f313600db621c.png)
11) Calcula a mano las siguientes raíces:
- 11a)
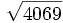
- 11b)

11) Calcula a mano las siguientes raíces:
- 11c)
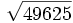
- 11d)
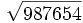
- 11e)
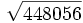
- 11f)
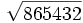
Actividades para que aprendas a calcular la raíz n-ésima de un número entero.
La raíz como potencia de exponente fraccionario
Proposición: La raíz como potencia de exponente fraccionario
Toda raíz se puede expresar como una potencia de la siguiente forma:
|
|
Basta con ver que se cumple la condición de la definición de raíz:
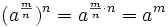
Ejemplo: La raíz como potencia de exponente fraccionario
Escribe las siguientes raíces como potencias de exponente fraccionario y calcula su valor:
a) 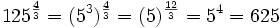
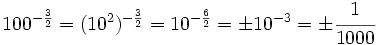 (por ser el índice par tiene dos soluciones de signos opuestos)
(por ser el índice par tiene dos soluciones de signos opuestos)Potencia de exponente fraccionario. Ejemplos.
Potencia de exponente fraccionario. Ejemplos.
Potencia de exponente fraccionario. Ejemplos.
Expresa como potencia de exponente fraccionario:
- a)
![\sqrt[5]{b^9}](/wikipedia/images/math/c/b/9/cb9fc88c51f111bf29a3da084ddafdb4.png)
- b)
![\sqrt[6]{g^5}](/wikipedia/images/math/b/8/2/b82a93b7500035423187e5a378387cc5.png)
- c)
![\cfrac{1}{\sqrt[7]{x}}](/wikipedia/images/math/7/1/1/711fca9584b1002a983e18467e624273.png)
Averigua el valor de a:
Averigua el valor de k:
Simplifica:
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Propiedades de las potencias de exponente fraccionario
Las potencias con exponente fraccionario tienen las mismas propiedades que con exponente natural o entero.
Calcula:
- a)
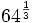
- b)
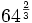
- c)
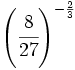
Calcula:
- a)
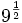
- b)
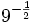
- c)
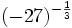
Calcula:
- a)
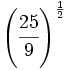
- b)
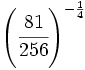
Calcula:
Simplifica:
Actividades para que aprendas a operar con raíces expresadas en forma de potencias de exponente fraccionario y a utilizar sus propiedades.
Simplifica expresiones radicales
Raíces exactas e inexactas
Se llaman raíces exactas de un número a aquellas que dan como resultado un número racional. En caso contrario diremos que son inexactas y el resultado será un número irracional.
Raíces exactas e inexactas
Para que una raíz sea exacta, al descomponer el radicando en factores primos, los exponentes de éstos deben ser todos divisibles por el índice de la raíz.
Ejemplo: Raíces exactas e inexactas
Calcula las siguientes raíces cuando sean exactas:
a) Descomponemos 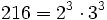 .
.
Como las potencias son divisibles por 3, la raíz es exacta. Para obtenerla, la regla práctica consiste en dividir cada exponente entre el índice. A continuación se explica el porqué de forma detallada:
![\sqrt[3]{216}=\sqrt[3]{2^3 \cdot 3^3}=(2^3 \cdot 3^3)^{\frac{1}{3}}=2^{\frac{3}{3}} \cdot 3^{\frac{3}{3}}=2^1 \cdot 3^1=6](/wikipedia/images/math/9/0/f/90ff62c218ce74b95403e00069fa46ec.png)
Luego ![\sqrt[3]{216}](/wikipedia/images/math/2/a/6/2a60cb9da80e1f9abad0623c37ccfb67.png) es racional.
es racional.
b) Descomponemos 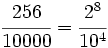 .
.
Como las potencias son divisibles por 4, la raíz es exacta. Para obtenerla, dividimos cada exponente entre el índice:
![\sqrt[4]{0.0256}=\sqrt[4]{\cfrac{256}{10000}}=\sqrt[4]{\cfrac {2^8}{10^4}}=\cfrac {2^{\frac{8}{4}}}{10^{\frac{4}{4}}}=\pm \cfrac{2^2}{10^1}=\pm \cfrac{4}{10}=\pm 0'4](/wikipedia/images/math/2/1/1/2111a7f15ed884cde82acb4bee2152c1.png)
Luego ![\sqrt[4]{0.0256}](/wikipedia/images/math/f/e/0/fe057f07425971a1f2db4869683fe6bd.png) es racional.
es racional.
c) Descomponemos 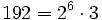 .
.
El exponente de 3 es 1, que no es divisible por 3. Por tanto, la raíz no es exacta.
Luego![\sqrt[3]{192}](/wikipedia/images/math/b/d/f/bdfe841e1073096ee42922125fc7e19d.png) es irracional.
es irracional.Tutorial que explica las raíces exactas e inexactas y pone ejemplos de ambas.
Raíces exactas:
Calcula:
- a)
![\sqrt[4]{16}](/wikipedia/images/math/0/8/5/08539911f08513b980a050e5bd399ead.png)
- b)
![\sqrt[5]{-243}](/wikipedia/images/math/6/3/5/635e97dd723ead900066d5383852216f.png)
Calcula:
- a)
![\sqrt[6]{64}](/wikipedia/images/math/4/7/2/472e429662dd1bbb544e8af33cf8e11b.png)
- b)
![\sqrt[3]{-216}](/wikipedia/images/math/1/9/0/1900c7889aa4b60b66f43b9dc348d52c.png)
Calcula:
- a)
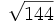
- b)
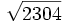
Raíces de fracciones
Cómo se calculan las raíces de fracciones. Ejemplos.
Cómo se suman y restan las raíces de fracciones. Ejemplos.
Cómo se multiplican raíces de fracciones. Ejemplos.
Cómo se dividen raíces de fracciones. Ejemplos.
Cómo se calculan las potencias de raíces de fracciones. Ejemplos.
Cómo se calculan las raíces de raíces de fracciones. Ejemplos.
Suma y resta de raíces de fracciones:
- 1)
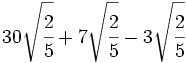
- 2)
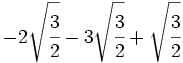
- 3)
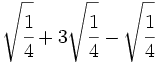
- 4)
![-\cfrac{1}{2}\sqrt[3]{\cfrac{-2}{3}}+\sqrt[3]{\cfrac{-2}{3}}-\cfrac{1}{4}\sqrt[3]{\cfrac{-2}{3}}](/wikipedia/images/math/f/5/5/f55a7abe041410d0d772b3f5f9249888.png)
- 5)
![-8\sqrt[3]{\cfrac{-3}{5}}+\cfrac{3}{2}\sqrt[3]{\cfrac{-3}{5}}-\cfrac{1}{4}\sqrt[3]{\cfrac{-3}{5}}](/wikipedia/images/math/c/7/e/c7e1346a8d6ef7ddeb7f7c7972383303.png)
Suma y resta de raíces de fracciones:
- 6)
![\sqrt[3]{\cfrac{-2}{3}}-\cfrac{1}{2}\sqrt[3]{\cfrac{-2}{3}}+2\sqrt[3]{\cfrac{-2}{3}}](/wikipedia/images/math/e/7/4/e74f2414908471712a21bcd2c0727973.png)
- 7)
![\sqrt[8]{\cfrac{9}{4}}+12\sqrt[8]{\cfrac{9}{4}}-\cfrac{1}{4}\sqrt[8]{\cfrac{9}{4}}](/wikipedia/images/math/7/9/5/7956651986adce493726a51fce226382.png)
- 8)
![\cfrac{-1}{3}\sqrt[11]{\cfrac{-3}{7}}+\cfrac{1}{9}\sqrt[11]{\cfrac{-3}{7}}-\cfrac{2}{3}\sqrt[11]{\cfrac{-3}{7}}](/wikipedia/images/math/f/c/e/fceb6863061e8ca281259ac86890e169.png)
- 9)
![-\sqrt[5]{\cfrac{5}{3}}-\cfrac{5}{2}\sqrt[5]{\cfrac{5}{3}}-\cfrac{1}{4}\sqrt[5]{\cfrac{5}{3}}](/wikipedia/images/math/9/2/2/92245797897977068795b35dc3cbcfc7.png)
Multiplicaciones de raíces de fracciones:
- 10)
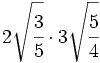
- 11)
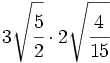
- 12)
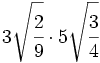
- 13)
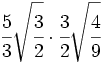
Multiplicaciones de raíces de fracciones:
- 14)
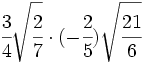
- 15)
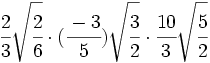
- 16)
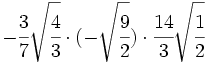
Multiplicaciones de raíces de fracciones:
- 17)
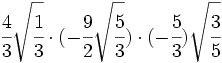
- 18)
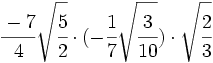
- 19)
![2\sqrt[3]{\cfrac{2}{5}} \cdot 3\sqrt[3]{\cfrac{4}{25}}](/wikipedia/images/math/f/8/1/f81614b373a70320fa5bbee491ded79d.png)
- 20)
![\sqrt[3]{\cfrac{9}{2}} \cdot \cfrac{5}{6}\sqrt[3]{\cfrac{2}{125}}](/wikipedia/images/math/f/d/b/fdbcdfd572102f2971190e92ad2b9ca8.png)
Multiplicaciones de raíces de fracciones:
- 21)
![\cfrac{-2}{5}\sqrt[3]{\cfrac{-1}{3}} \cdot 5\sqrt[3]{\cfrac{-1}{9}}](/wikipedia/images/math/e/1/d/e1dc683585b12c3e8f8b0336e6cd3dce.png)
- 22)
![2\sqrt[3]{\cfrac{7}{3}} \cdot \cfrac{1}{4}\sqrt[3]{\cfrac{9}{14}}](/wikipedia/images/math/4/e/5/4e5561c3d3d0f4cadb26ebea76193f5e.png)
- 23)
![8\sqrt[3]{\cfrac{3}{7}} \cdot \sqrt[3]{\cfrac{-7}{9}} \cdot \sqrt[3]{\cfrac{-7}{2}}](/wikipedia/images/math/9/9/9/99904e001c4c05d9a33cc7f20320c6eb.png)
Multiplicaciones de raíces de fracciones:
- 24)
![3\sqrt[3]{\cfrac{9}{4}} \cdot \left( -\cfrac{1}{2}\sqrt[3]{\cfrac{3}{2}} \right) \cdot \cfrac{2}{5}\sqrt[3]{125}](/wikipedia/images/math/d/3/c/d3cb69b0f72a7fed15f71aa8513dfbb6.png)
- 25)
![\cfrac{4}{3}\sqrt[4]{\cfrac{3}{7}} \cdot 3\sqrt[4]{\cfrac{16}{3}}](/wikipedia/images/math/b/d/5/bd5b5b76b496c2f6825e62489c158052.png)
- 26)
![\cfrac{1}{3}\sqrt[8]{\cfrac{1}{4}} \cdot \left( -\cfrac{9}{2}\sqrt[8]{\cfrac{2}{3}} \right) \cdot 4\sqrt[8]{\cfrac{3}{5}}](/wikipedia/images/math/7/4/4/74408c6f3e91a102054dcf8b4a208595.png)
División de raíces de fracciones:
- 27)
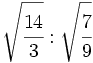
- 28)
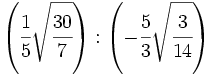
- 29)
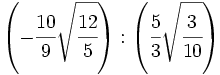
- 30)
![\left( -\cfrac{2}{3}\sqrt[3]{\cfrac{14}{5}} \right): \left( \cfrac{14}{12}\sqrt[3]{\cfrac{7}{10}} \right)](/wikipedia/images/math/a/9/1/a913d1108fd67aec4f52e62b81efa9e8.png)
División de raíces de fracciones:
- 31)
![\left( \cfrac{9}{2}\sqrt[3]{\cfrac{14}{9}} \right) : \left( \sqrt[3]{\cfrac{-7}{3}} \right)](/wikipedia/images/math/8/9/e/89e41ac40d647d9d9d10fd9f080b8f9c.png)
- 32)
![\left( \cfrac{12}{5}\sqrt[3]{\cfrac{18}{3}} \right): \left( -\cfrac{6}{5}\sqrt[3]{\cfrac{-9}{2}} \right)](/wikipedia/images/math/7/8/b/78b4e0f5d87c167f3b7d0e410f45c6ec.png)
División de raíces de fracciones:
- 33)
![\left( -\cfrac{10}{3}\sqrt[4]{\cfrac{15}{49}} \right) : \left( \cfrac{5}{27}\sqrt[4]{\cfrac{49}{125}} \right)](/wikipedia/images/math/a/6/4/a64ae58b74db2719880d0c4bceb986c7.png)
- 34)
![\left( -\cfrac{10}{4}\sqrt[5]{\cfrac{15}{7}} \right): \left( \cfrac{5}{6}\sqrt[5]{\cfrac{5}{14}} \right)](/wikipedia/images/math/9/4/7/9479dbe129a893330d386ef04c8dddcb.png)
- 35)
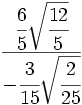
División de raíces de fracciones:
- 36)
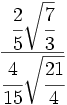
- 37)
![\cfrac{-\cfrac{10}{7}\sqrt[3]{\cfrac{15}{4}}}{5\sqrt[3]{\cfrac{8}{9}}}](/wikipedia/images/math/3/f/7/3f7ec32f3c77881d616b8760375d4d6f.png)
- 38)
![\cfrac{-\cfrac{10}{6}\sqrt[3]{\cfrac{15}{4}}}{\cfrac{5}{3}\sqrt[3]{\cfrac{2}{25}}}](/wikipedia/images/math/2/f/5/2f578dac94a33d0ddc501f0c60f4fffb.png)
Potencias de raíces de fracciones:
- 39)
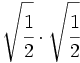
- 40)
![\sqrt[3]{\cfrac{-1}{5}} \cdot \sqrt[3]{\cfrac{-1}{5}} \cdot \sqrt[3]{\cfrac{-1}{5}}](/wikipedia/images/math/6/3/9/63995d3707778bdb86de378c75aca586.png)
- 41)
![\sqrt[3]{\cfrac{2}{3}} \cdot \sqrt[3]{\cfrac{2}{3}} \cdot \sqrt[3]{\cfrac{2}{3}}](/wikipedia/images/math/6/3/3/633c62efe0db98851d8196c7d058cbe0.png)
- 42)
![\sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}}](/wikipedia/images/math/9/0/e/90e63a779d9f738b1332ad73f20d0c44.png)
- 43)
![\sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}}](/wikipedia/images/math/9/f/0/9f0f9afc0dba273231a5b490e098027d.png)
Convierte en potencias de exponente fraccionario:
- 44)
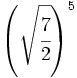 ; 45)
; 45) 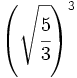 ; 46)
; 46) 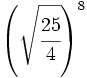
- 47)
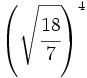 ; 48)
; 48) 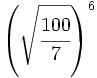 ; 49)
; 49) ![\left( \sqrt[3]{\cfrac{7}{3}} \right)^6](/wikipedia/images/math/7/6/3/763844586d27849f01b0f220f197d4d0.png)
- 50)
![\left( \sqrt[3]{\cfrac{5}{2}} \right)^9](/wikipedia/images/math/5/b/7/5b7af58a06ea229f4169c8f038eeb6a0.png) ; 51)
; 51) ![\left( \sqrt[4]{\cfrac{7}{4}} \right)^8](/wikipedia/images/math/0/e/0/0e0e0fafb99b320da94e2293f4f14701.png) ; 52)
; 52) ![\left( \sqrt[6]{\cfrac{21}{5}} \right)^{12}](/wikipedia/images/math/a/0/7/a07d93d0c3029249c9933a99a2eb2728.png)
- 53)
![\left( \sqrt[21]{\cfrac{12}{5}} \right)^{14}](/wikipedia/images/math/5/5/3/55309d54139afb8fbea7172261e4f109.png)
Convierte la potencia en raíz:
- 54)
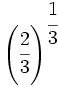 ; 55)
; 55) 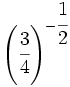 ; 56)
; 56) 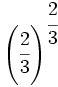
- 57)
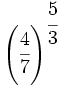 ; 58)
; 58) 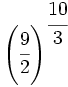 ; 59)
; 59) 
Raíces de una raíz de una fracción:
- 60)
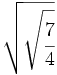 ; 61)
; 61) 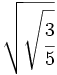 ; 62)
; 62) 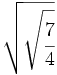
- 63)
![\sqrt[3]{\sqrt{\cfrac{2}{5}}}](/wikipedia/images/math/f/e/9/fe9d5ed19933ef100bc8b0f67559fa52.png) ; 64)
; 64) ![\sqrt[3]{\sqrt[3]{\cfrac{25}{4}}}](/wikipedia/images/math/7/b/3/7b3a4b58a2b91246bf250ff1abd743b3.png) ; 65)
; 65) ![\sqrt{\sqrt[3]{64}}](/wikipedia/images/math/0/e/d/0eddc7f2593e00fd623113cf77aff52f.png)
- 66)
![\sqrt[4]{\sqrt[3]{\cfrac{2}{7}}}](/wikipedia/images/math/e/b/e/ebedfae4b0471be70ea604bbe26e5e19.png) ; 67)
; 67) ![\sqrt[3]{\sqrt{\cfrac{12}{5}}}](/wikipedia/images/math/2/f/5/2f5c1b5dfc0e771272ee1b0c8e2ac6db.png)
Calculadora
Raíz cuadrada
|
Calculadora: Raíz cuadrada |
Raíz cúbica
|
Calculadora: Raíz cúbica |
Otras raíces
|
Calculadora: Otras raíces |
Radical
- Un radical es cualquier expresión del tipo:
![k \cdot \sqrt[n]{a}~,~k \in \mathbb{R}](/wikipedia/images/math/c/2/6/c26445b313b501056047ed7787606a37.png)
- Si dos radicales tienen el mismo índice diremos que son homogéneos.
- Si dos radicales tienen el mismo índice y el mismo radicando diremos que son semejantes.
Radicales: homogéneos y semejantes. Ejemplos.
Radicales equivalentes
Dos o más radicales son equivalentes si se pueden poner como potencias de exponente fraccionario con la misma base y cuyos exponentes sean fracciones equivalentes.
Actividades en las que podrás aprender lo que son radicales equivalentes y cómo obtener radicales equivalentes con un índice superior (amplificación) o inferior (simplificación)
Ejercicios de autoevaluación sobre radicales equivalentes.
Reducción de radicales a índice común
La amplificación y simplificación de radicales nos va a permitir reducir radicales a índice común realizando el mínimo común múltiplo de los índice al igual que para reducir fracciones a común denominador se hacía el m.c.m. de los denominadores. No olvidemos que índice y denominador del exponente es lo mismo.
Reducción de radicales a índice común. Ejemplos.
Ejercicios de autoevaluación sobre reducción de radicales a índice común.
Ordenación de radicales
La reducción de radicales a índice común nos va a permitir ordenar cómodamente varios radicales:
Ordenación de radicales. Ejemplos.
Operaciones con radicales
Propiedades de las operaciones con radicales
Propiedades de las operaciones con radicales
1. ![\sqrt[np]{a^p}=\sqrt[n]{a}](/wikipedia/images/math/1/9/0/19055926ec943d41884a4e4efb9e3958.png)
2. ![\left ( \sqrt[n]{a}\right )^p=\sqrt[n]{a^p}](/wikipedia/images/math/0/8/f/08f48fff6b28e5860652ad48624e9b54.png)
3. ![\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}](/wikipedia/images/math/8/8/2/882098878748f7e317a403bacf091e37.png)
4. ![\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a \cdot b}](/wikipedia/images/math/7/3/d/73d577cd0a118df1dda404e72e4a922d.png)
5. ![\cfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\cfrac{a}{b}}](/wikipedia/images/math/4/8/d/48d4191b86a6079638a33f860884bd8e.png)
Para demostrar estas propiedades basta con expresar el radical como potencia de exponente fraccionario y aplicar sus propiedades.
Ejercicios resueltos: Radicales. Propiedades
Simplificar: a) ![\sqrt[12]{x^9}](/wikipedia/images/math/9/4/2/942b2336ccb4cf42b2cbd07ed9c75ede.png) , b)
, b) ![\left ( \sqrt[3]{a^2} \right )^6](/wikipedia/images/math/9/a/1/9a1db4aea08869857d67618e54707551.png) , c)
, c) ![\sqrt{\sqrt[3]{a}}](/wikipedia/images/math/4/7/3/473cf1ea29276b3cfe84680bf3548a10.png) , d)
, d) ![\sqrt[3]{3} \cdot \sqrt[3]{9}](/wikipedia/images/math/6/d/2/6d24beca08bdb942089cf6ad8b4c7d1c.png) , e)
, e) 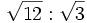
a) ![\sqrt[12]{x^9}=\sqrt[4 \cdot 3]{x^{3 \cdot 3}}=\sqrt[4]{x^{3}}](/wikipedia/images/math/d/1/9/d190b659acadff5f242846e5d6014e10.png) , usando la propiedad nº 1.
, usando la propiedad nº 1.
b) ![\left ( \sqrt[3]{a^2} \right )^6=\sqrt[3]{a^{12}}=a^{\frac{12}{3}}=a^4](/wikipedia/images/math/9/4/b/94b477fe13f98eac4d76261cf2c34d2c.png) , usando la propiedad nº 2 y transformando el radical en potencia de exponente fraccionario.
, usando la propiedad nº 2 y transformando el radical en potencia de exponente fraccionario.
c) ![\sqrt{\sqrt[3]{a}}=\sqrt[2 \cdot 3]{a}=\sqrt[6]{a}](/wikipedia/images/math/9/4/a/94ad123ac81d4cf1d017be5a726de942.png) , usando la propiedad nº 3.
, usando la propiedad nº 3.
d) ![\sqrt[3]{3} \cdot \sqrt[3]{9}= \sqrt[3]{3 \cdot 9} =\sqrt[3]{27}=3](/wikipedia/images/math/b/7/b/b7b21e3525e1caa80c30fe91bbb85c77.png) , usando la propiedad nº 4.
, usando la propiedad nº 4.
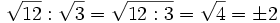 , usando la propiedad nº 5.
, usando la propiedad nº 5.Actividades en las que podrás aprender las propiedades de las operaciones con radicales del mismo índice.
Tutorial que explica las propiedades básicas de los radicales, con ejemplos resueltos.
Propiedades de las operaciones con radicales. Ejemplos.
Propiedades de las operaciones con radicales. Ejemplos.
Propiedades de las operaciones con radicales. Ejemplos.
Propiedades de las operaciones con radicales. Ejemplos.
Ejemplos sencillos de aplicación de las propiedades de las operaciones con radicales.
Simplifica: 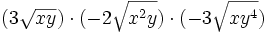
Simplifica: ![(-8\sqrt[3] {x^{10}y^2}) : (-4\sqrt[3] {xy^{11}})](/wikipedia/images/math/2/1/b/21b675f2e891ca1cd137acdf888cbcde.png)
Calcula: ![\sqrt[4]{\cfrac{81}{16}}](/wikipedia/images/math/9/e/d/9ed2bdc3b33dce510e788cce2d6938b7.png)
Calcula:
1) 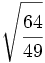 2)
2) ![\sqrt[4]{\cfrac{1}{81}}](/wikipedia/images/math/a/5/4/a54618bf9ee77a830fab9a825f43fad0.png) 3)
3) ![\sqrt[3]{\cfrac{-27~~}{125}}](/wikipedia/images/math/5/c/3/5c3b48c07709122b11aadf157c159924.png) 4)
4) ![\sqrt[5]{\cfrac{-32~~}{243}}](/wikipedia/images/math/7/5/8/758e101bb00fde536dd8dc589f2eab1d.png)
Suma y resta de radicales semejantes
Para sumar y restar radicales, éstos deben ser semejantes, es decir, tener el mismo radicando y el mismo índice. En tal caso el radical el radical resultante tiene como coeficiente la suma o resta de los coeficientes de cada uno de los radicales.
Ejemplo: Suma y resta de radicales semejantes
Efectúa las siguientes sumas y restas de radicales:
1. 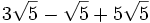
2. 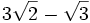
3. ![3\sqrt[3]{2}+\sqrt{2}](/wikipedia/images/math/f/5/5/f554a76b3698de9bd3d86d6600364c25.png)
1. 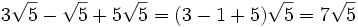
2. 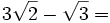 (No se puede simplificar)
(No se puede simplificar)
![3\sqrt[3]{2}+\sqrt{2}=](/wikipedia/images/math/a/6/e/a6edb4be927bfe44dff1ae00ac0eb772.png) (No se puede simplificar)
(No se puede simplificar)Actividades
En los siguientes videotutoriales vamos a repasar las operaciones con radicales vistas hasta ahora, antes de pasar a ver otros casos de mayor dificultad.
- Definición de radical y de radicales semejantes.
- Suma de radicales semejantes.
- Radicales opuestos.
- Resta de radicales semejantes.
- Producto de radicales del mismo índice.
- División de radicales del mismo índice.
- Potencia de un radical.
- Raíz de un radical.
1) Radicales semejantes:
- 1a) Escribe tres radicales semejantes y tres que no lo sean.
- 1b) Escribe dos radicales semejantes opuestos.
2) Calcula:
- 2a)
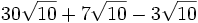
- 2b)
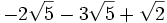
- 2c)
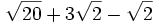
- 2d)
![-3 \sqrt[3]{11}+\sqrt[3]{11}-8 \sqrt[3]{11}\;](/wikipedia/images/math/3/8/6/386dda78a1c0a8e06a7d92ad446cca8a.png)
- 2e)
![-8 \sqrt[3]{11}+4 \sqrt[3]{11}-2 \sqrt[3]{11}\;](/wikipedia/images/math/9/b/c/9bc9cc4fe2abf85a102fd7edd8a91a3e.png)
- 2f)
![\sqrt[3]{-5}-5 \sqrt[3]{-5}+2 \sqrt[3]{-5}\;](/wikipedia/images/math/7/9/7/797db9d9f2a327215cf66dc0fd1a0989.png)
- 2g)
![6 \sqrt[8]{3}+12 \sqrt[8]{3}-4 \sqrt[8]{3}\;](/wikipedia/images/math/e/a/3/ea3c1128b9341e9ee92e9adf7dbf36e8.png)
- 2h)
![5 \sqrt[11]{-8}+9 \sqrt[11]{-8}- \sqrt[11]{-8}\;](/wikipedia/images/math/c/f/c/cfc360decb13c219ecfed5246e616bbc.png)
- 2i)
![-\sqrt[5]{3}- \sqrt[5]{3}-4 \sqrt[5]{3}\;](/wikipedia/images/math/c/d/0/cd013a1ff11c225a935a2891232efb7a.png)
3) Halla el opuesto de los siguiente radicales y después suma cada radical con su opuesto:
- 3a)
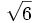
- 3b)

- 3c)
![-5\sqrt[3]{2}\;](/wikipedia/images/math/2/9/b/29ba151ca92717a7ec2fce60d9a43887.png)
- 3d)
![-8\sqrt[3]{-3}\;](/wikipedia/images/math/4/4/a/44af796a04099974506078fbdaa97c8e.png)
- 3e)
![14\sqrt[3]{5}\;](/wikipedia/images/math/a/8/b/a8b18bd1e94168e14bdfa178486c55de.png)
- 3f)
![-5\sqrt[4]{7}\;](/wikipedia/images/math/9/c/3/9c3b71fe66e4cd559e4c1c3e2d8f0d50.png)
4) Calcula:
- 4a)
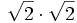
- 4b)
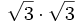
- 4c)
![\sqrt[3]{2} \cdot \sqrt[3]{2} \cdot \sqrt[3]{2} \;](/wikipedia/images/math/8/b/7/8b72eb2e695638b1b598aa91906d2afd.png)
- 4d)
![\sqrt[3]{5} \cdot \sqrt[3]{5} \cdot \sqrt[3]{5} \;](/wikipedia/images/math/4/7/0/4706a180f7cecca86f552cb03bc61723.png)
- 4e)
![\sqrt[4]{3} \cdot \sqrt[4]{3} \cdot \sqrt[4]{3} \cdot \sqrt[4]{3} \;](/wikipedia/images/math/8/7/1/871aec8b9c551d588f6bb0f7652776b0.png)
- 4f)
![\sqrt[6]{7} \cdot \sqrt[6]{7} \cdot \sqrt[6]{7} \cdot \sqrt[6]{7} \cdot \sqrt[6]{7} \cdot \sqrt[6]{7} \;](/wikipedia/images/math/c/6/1/c61ef44eacb7a1efa0af29b13e778c84.png)
- 4g)
![\sqrt[5]{-2} \cdot \sqrt[5]{-2} \cdot \sqrt[5]{-2} \cdot \sqrt[5]{-2} \cdot \sqrt[5]{-2}\;](/wikipedia/images/math/b/a/a/baaf1e13d7ae13183caee280ed997078.png)
- 4h)
![\sqrt[7]{-7} \cdot \sqrt[7]{-7} \cdot \sqrt[7]{-7} \cdot \sqrt[7]{-7} \cdot \sqrt[7]{-7} \cdot \sqrt[7]{-7} \cdot \sqrt[7]{-7} \;](/wikipedia/images/math/3/0/4/3044aa9fbabf7c1d05d005d3d067c642.png)
- 4i)
![\sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \cdot \sqrt[8]{6} \;](/wikipedia/images/math/f/2/4/f24f9a63eafe40b3e6d366a5e52f6be1.png)
- 4j)
![\sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2} \cdot \sqrt[10]{2}\;](/wikipedia/images/math/5/6/9/5699ece51e33ce84d469d13405c1a662.png)
5) Calcula:
- 5a)
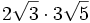
- 5b)
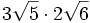
- 5c)
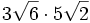
- 5d)
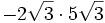
- 5e)
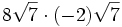
- 5f)
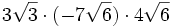
- 5g)
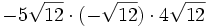
- 5h)
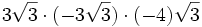
- 5h)
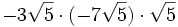
5) Calcula:
- 5i)
![2\sqrt[3]{3} \cdot 3\sqrt[3]{3} \;](/wikipedia/images/math/e/b/8/eb885ee9f22a7b60f1fba48b165a9bba.png) ; 5j)
; 5j) ![3\sqrt[3]{5} \cdot 2\sqrt[3]{5} \;](/wikipedia/images/math/7/4/8/74817e09bd26600d541bc7f27acc2721.png) ; 5k)
; 5k) ![3\sqrt[3]{6} \cdot 5\sqrt[3]{6} \;](/wikipedia/images/math/4/d/7/4d731dfeb72737e5ea4b3fae68d986bc.png)
- 5l)
![-2\sqrt[3]{3} \cdot 5\sqrt[3]{3} \;](/wikipedia/images/math/b/d/0/bd0bdd2316e3647e561f42eea5e49432.png) ; 5m)
; 5m) ![8\sqrt[3]{-7} \cdot \sqrt[3]{-2} \cdot \sqrt[3]{-7} \;](/wikipedia/images/math/d/e/6/de6d9da92635aa3ed672a1d37bbb9d1e.png) ; 5n)
; 5n) ![3\sqrt[3]{3} \cdot (-7\sqrt[3]{3}) \cdot 4\sqrt[3]{3} \;](/wikipedia/images/math/8/d/7/8d7ab02625222fb400fbef68aae4f1a9.png)
- 5o)
![-5\sqrt[3]{12} \cdot (-\sqrt[3]{12}) \cdot 4\sqrt[3]{12} \;](/wikipedia/images/math/2/4/d/24db05991b4866bee0cf063c06a2a5a4.png) ; 5p)
; 5p) ![3\sqrt[3]{3} \cdot (-3\sqrt[3]{3}) \cdot (-4\sqrt[3]{3}) \;](/wikipedia/images/math/0/b/1/0b12fb80b6b5d9ab9cff8bdda29e3670.png) ; 5q)
; 5q) ![-3\sqrt[3]{5} \cdot (-7\sqrt[3]{5}) \cdot \sqrt[3]{5} \;](/wikipedia/images/math/4/9/3/493e61292a0c10080a211793ad3d938a.png)
6) Calcula:
- 6a)
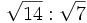 ; 6b)
; 6b) 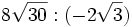 ; 6c)
; 6c) 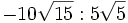
- 6d)
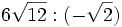 ; 6e)
; 6e) 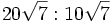 ; 6f)
; 6f) ![\sqrt[3]{14} : \sqrt[3]{7} \;](/wikipedia/images/math/e/5/5/e55782cffbcf990bcc3401f1a26c47b6.png)
- 6g)
![9\sqrt[3]{14} : (-\sqrt[3]{-7}) \;](/wikipedia/images/math/e/a/6/ea6ac7a2061e05e92f94b80d4af19663.png) ; 6h)
; 6h) ![-10\sqrt[3]{15} : 5\sqrt[3]{5} \;](/wikipedia/images/math/c/3/0/c308580a14622890c46723f7fdf783fb.png) ; 6i)
; 6i) ![12\sqrt[3]{18} : (-6\sqrt[3]{-9}) \;](/wikipedia/images/math/0/5/9/05982cd16e41d3ae4cdc9d011905ad4b.png)
- 6j)
![-30\sqrt[3]{14} : 6\sqrt[3]{7} \;](/wikipedia/images/math/0/0/9/00930632b62d29b0446beb2eb4585c39.png) ; 6k)
; 6k) ![\sqrt[4]{14} : \sqrt[4]{7} \;](/wikipedia/images/math/3/7/d/37d6db29364ddf586bf938556c44bf69.png) ; 6l)
; 6l) ![9\sqrt[4]{14} : (-\sqrt[4]{7}) \;](/wikipedia/images/math/c/1/2/c12d93323a255c0807c702a7d1c4fd3a.png)
- 6m)
![-10\sqrt[4]{15} : 5\sqrt[4]{5} \;](/wikipedia/images/math/f/b/4/fb47b8279375acea84ad3b6776fe52d9.png) ; 6n)
; 6n) ![12\sqrt[4]{18} : (-6\sqrt[4]{9}) \;](/wikipedia/images/math/0/e/e/0ee9a8d792aa42be622074880b8c1737.png) ; 6o)
; 6o) ![-30\sqrt[4]{14} : 6\sqrt[4]{7}) \;](/wikipedia/images/math/f/8/6/f86747fe7edf79f2f565ae3b47c5f5cc.png)
- 6p)
![\sqrt[5]{14} : \sqrt[5]{7} \;](/wikipedia/images/math/c/e/d/cedeedebf22023c7095857fdb5f89cd9.png) ; 6q)
; 6q) ![9\sqrt[5]{14} : (-\sqrt[5]{7}) \;](/wikipedia/images/math/a/0/8/a0809badb27cd335d6d595e07efabe29.png) ; 6r)
; 6r) ![-10\sqrt[5]{15} : 5\sqrt[5]{5}) \;](/wikipedia/images/math/b/9/9/b99dbf9eb1bd9e64b5651116476d3105.png)
7) Calcula:
- a)
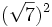 ; b)
; b) ![(\sqrt[3]{7})^3\;](/wikipedia/images/math/e/3/6/e3645d99093cd9065fb2082d8c6c6c01.png) ; c)
; c) ![(\sqrt[4]{7})^4\;](/wikipedia/images/math/8/4/f/84f808c115fe3de548ae9bfe5824709f.png) ; d)
; d) 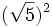 ; e)
; e) ![(\sqrt[3]{5})^3\;](/wikipedia/images/math/f/2/b/f2bf6748d06d16bcaae81f483dfd71c9.png)
- f)
![(\sqrt[4]{21})^4\;](/wikipedia/images/math/d/e/7/de71424f30904a433e21926aea5c19ea.png) ; g)
; g) 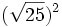 ; h)
; h) ![(\sqrt[3]{-25})^3\;](/wikipedia/images/math/4/7/8/478cc6706fac0d47cfc87e4c40c1a9fa.png) ; i)
; i) ![(\sqrt[4]{100})^4\;](/wikipedia/images/math/6/1/d/61d8bd6207295d4b3de801045656acdb.png) ; j)
; j) 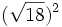
- k)
![(\sqrt[3]{-100})^3\;](/wikipedia/images/math/e/1/6/e16420641a6f36c33546ff527203864c.png) ; l)
; l) ![(\sqrt[5]{16})^5\;](/wikipedia/images/math/8/0/2/802fdd52c9cc6b2275f4ecb0a8ca4ae1.png) ; m)
; m) 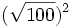 ; n)
; n) ![(\sqrt[3]{18})^3\;](/wikipedia/images/math/b/c/c/bcc549d18d80fd5c5888a59db21937bf.png) ; o)
; o) ![(\sqrt[6]{12})^6\;](/wikipedia/images/math/5/9/7/597c0afad70f17b1f3788787dfd0974a.png)
8) Calcula:
- a)
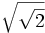 ; b)
; b) 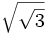 ; c)
; c) 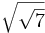 ; d)
; d) ![\sqrt[3]{\sqrt{2}}\;](/wikipedia/images/math/5/7/5/5750c75c078868e9954cfd490001321d.png)
- e)
![\sqrt[3]{\sqrt[3]{25}}\;](/wikipedia/images/math/a/6/1/a61140b4f250a3cb23f5d4156fc505bd.png) ; f)
; f) ![\sqrt{\sqrt[3]{64}}\;](/wikipedia/images/math/e/2/3/e23312ed4b7fe23d8f48d5afad9e73be.png) ; g)
; g) ![\sqrt[4]{\sqrt[3]{2}}\;](/wikipedia/images/math/1/7/7/17747fd8e1ef3646625fd5f03e380c01.png) ; h)
; h) ![\sqrt[3]{\sqrt{128}}\;](/wikipedia/images/math/1/7/e/17e0360d6aab8d041cd7f8c090dbc6c1.png)
Extracción e introducción de factores en un radical
El siguiente videotutorial resume lo que se va a a ver en este apartado:
Tutorial que explica cómo extraer factores de un radical, que se utiliza principalmente para simplificar radicales, y de cómo introducir factores dentro.
Extracción de factores
Procedimiento
Para extraer factores de un radical se divide el exponente (m) del factor entre el índice (n) del radical. A continuación, se saca el factor elevado al cociente (c) de la división, quedando dentro del radical el factor elevado al resto (r).
![\sqrt[n]{a^m}= a^c \cdot \sqrt[n]{a^r}](/wikipedia/images/math/5/e/c/5ecb8e4f6515ae774c6eef7fea5c576e.png)
Para la demostración transformaremos la expresión radical en potencias y aplicaremos las propiedades de las operaciones con potencias:
Fíjate que en (1) hemos usado la regla de la divsión:
Para extraer factores de un radical se divide el exponente entre el índice y se saca el factor elevado al cociente de la división quedando ese factor elevado al resto.
Ejemplo: Extracción de factores de un radical
Extrae todo lo que se pueda de este radical: ![\sqrt[3]{6000}](/wikipedia/images/math/5/c/2/5c28fba2f76ed7b33ea1b13e448c224f.png)
![\sqrt[3]{6000}=\sqrt[3]{2^4 \cdot 3 \cdot 5^3}=2 \cdot 5 \sqrt[3]{2 \cdot 3}=10\sqrt[3]{6}](/wikipedia/images/math/6/9/f/69fad43d23404b125d2e89b1f9479c74.png)
Extracción de factores de un radical. Ejemplos.
Extracción de factores de un radical utilizando un símil curioso.
Extracción de factores de un radical. Ejemplos
Extracción de factores de un radical.
Simplifica: a) Simplifica: a) Simplifica: a) Simplifica: a) Simplifica: a) Simplifica: a) Simplifica: Simplifica: Simplifica: | Simplifica: Extrae todos los factores posibles del radicando:
Extrae todos los factores posibles del radicando:
Simplifica: Simplifica: Simplifica:
Simplifica: Simplifica: Simplifica: |
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Extrae factores fuera del radical.
Extrae factores fuera del radical.
Extrae factores fuera del radical (con variables).
Extrae factores fuera del radical (con variables).
Introducción de factores
Procedimiento
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical.
![a \sqrt[n]{b}= \sqrt[n]{a^n \cdot b}](/wikipedia/images/math/8/5/f/85f82704cfc0f9e1418d853a9e18061d.png)
Para la demostración transformaremos la expresión radical en potencias y aplicaremos las propiedades de las operaciones con potencias:
Ejemplo: Introducción de factores en un radical
Introduce los factores dentro del radical: ![10 \sqrt[3]{6}](/wikipedia/images/math/b/0/5/b059e301f3cf30968be2c858922be777.png)
![10 \sqrt[3]{6}=\sqrt[3]{6 \cdot 10^3}=\sqrt[3]{6000}](/wikipedia/images/math/f/c/a/fca24b7a66a69b8d0a52ef1d1f43ef96.png)
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Introduce dentro del radical: 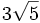
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical. De esta manera, y teniendo en cuenta las propiedades de las operaciones con potencias, para introducir una potencia dentro de un radical multiplicaremos el exponente de la potencia por el índice del radical. La potencia resultante pasará dentro del radical multiplicando al radicando.
Introduce los factores dentro del radical: ![a^3 b^2 \sqrt[4]{c}](/wikipedia/images/math/0/f/2/0f257d67a28e35c2fe66d6e47ec6170b.png)
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical. De esta manera, y teniendo en cuenta las propiedades de las operaciones con potencias, para introducir una potencia dentro de un radical multiplicaremos el exponente de la potencia por el índice del radical. La potencia resultante pasará dentro del radical multiplicando al radicando.
Introduce los factores dentro del radical: ![m^2 n^5 \sqrt[5]{m^3 p^2}](/wikipedia/images/math/2/7/6/276aa6fd087cafe6e44377e54dfae158.png)
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical. De esta manera, y teniendo en cuenta las propiedades de las operaciones con potencias, para introducir una potencia dentro de un radical multiplicaremos el exponente de la potencia por el índice del radical. La potencia resultante pasará dentro del radical multiplicando al radicando. Si dentro del radical tenemos otra potencia con la misma base entonces sumaremos el exponente de la potencia que entra con el de dentro del radical.
Introduce factores dentro del radical:
- a)
![4 \sqrt[3]{6}](/wikipedia/images/math/0/9/8/09832a2fdbea98af094bc3b99a2f71fb.png)
- b)
![2^4 \cdot 3^2 \sqrt[6]{2^2 \cdot 3^5}](/wikipedia/images/math/a/3/e/a3e7fc4c36dc72ff46d3e14c87570f8c.png)
- b)
![a^7 \cdot b^8 \sqrt[5]{b^2}](/wikipedia/images/math/7/1/c/71c6e44e4a1a1f816fefc0e45b931acc.png)
Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien.
Ejercicios de autoevaluación sobre introducción y extracción de factores de un radical.
Suma y resta de radicales con el mismo índice y distinto radicando
Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando.
Ejemplo: Suma y resta de radicales con el mismo índice y distinto radicando
Resta los siguientes radicales: 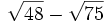
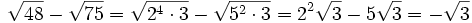
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Tutorial que explica cómo sumar y restar radicales. La suma y resta son operaciones que "se llevan muy mal" con el resto de operaciones y hay que tener mucho cuidado a la hora de hacerlo con radicales.
Suma y resta de radicales con el mismo índice. Ejemplos.
Simplifica: 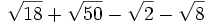
Simplifica: 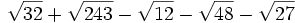
Calcula:
- a)
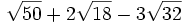
- b)
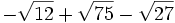
- c)
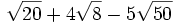
- d)
![\sqrt[3]{48}+\sqrt[3]{1080}-\sqrt[3]{96}\;](/wikipedia/images/math/2/d/6/2d67b353649768215c317a719b4f248d.png)
- e)
![-\sqrt[3]{-27}+2\sqrt[3]{272}-9\sqrt[3]{-81}\;](/wikipedia/images/math/c/0/f/c0ff906569b1db6871629962fc420418.png)
Calcula:
- a)
![\sqrt[4]{32}+8\sqrt[4]{16}-\sqrt[4]{80}\;](/wikipedia/images/math/4/c/a/4cac9ae91631e9811be06e223293e340.png)
- b)
![\sqrt[5]{64}-6\sqrt[5]{32}+5\sqrt[5]{96}\;](/wikipedia/images/math/7/a/f/7af16a27ecbd28162b9ffd8bcc06a665.png)
- c)
![-9\sqrt[6]{64}+\sqrt[6]{192}-\sqrt[6]{960}\;](/wikipedia/images/math/4/5/c/45c6fc0df3cf3b4245b56dcf055735ec.png)
Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien.
Producto y cocientes de radicales con distinto índice
Para multiplicar o dividir radicales con distinto índice, primero se reducen a índice común y luego se multiplican o dividen los radicandos.
Ejemplo: Producto y cocientes de radicales con distinto índice
Reduce a un solo radical ![\sqrt[3]{10} \cdot \sqrt[4]{5}:\sqrt{8}](/wikipedia/images/math/5/9/7/597ebbc8a8a1e63faeabbecf3da740ef.png)
Para reducir los radicales a índice común calculamos el m.c.m de los índices: m.c.m.(3,4,2)=12 y elevamos cada radicando al resultado de dividir el m.c.m. por el índice de cada radical.
![\sqrt[3]{10} \cdot \sqrt[4]{5}:\sqrt{8}=\sqrt[12]{10^4} \cdot \sqrt[12]{5^3}:\sqrt[12]{8^6}](/wikipedia/images/math/e/8/1/e81ffde8d1c752d66e97b66e25149a0f.png)
Luego multiplicamos o dividimos los radicandos, ya que ahora los índices son iguales:
![\sqrt[12]{10^4} \cdot \sqrt[12]{5^3}:\sqrt[12]{8^6}=\sqrt[12]{10^4 \cdot 5^3 : 8^6}](/wikipedia/images/math/6/d/1/6d1f82fd6b85971e0e493c1e7eb2d485.png)
Finalmente simplificamos:
![\sqrt[12]{10^4 \cdot 5^3 : 8^6}=\sqrt[12]{2^4 \cdot 5^4 \cdot 5^3 : (2^3)^6}=\sqrt[12]{2^{-14} \cdot 5^7}](/wikipedia/images/math/7/0/e/70e1e7afd0d65ac459a2b76336b7fbb6.png)
Producto y cociente de radicales con el mismo o con distinto índice. Ejemplos.
Simplifica: ![(8\sqrt[3]{a^2b}) \cdot (4\sqrt{ab^3})](/wikipedia/images/math/8/e/a/8ea372bbacf499b888b5f31aeb1cae8b.png)
Simplifica: ![\sqrt[3]{27^{-2}} : \sqrt[4]{16}](/wikipedia/images/math/1/0/d/10dcb2912a1fddcdb4f0013df23cedc3.png)
Actividades en las que podrás aprender a multiplicar y dividir radicales de distinto índice previa reducción a índice común.
Ejercicios de autoevaluación sobre productos de radicales.
Ejercicios de autoevaluación sobre cocientes de radicales.
Potencias de radicales
Potencias de radicales. Ejemplos.
Ejercicios de autoevaluación sobre potencias de radicales.
Radicales dobles (Avanzado)
Convierte los siguientes radicales dobles en sencillos:
a) 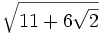
b) 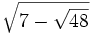
Convierte los siguientes radicales dobles en sencillos:
a) 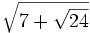
b) 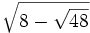
Convierte los siguientes radicales sencillos en dobles:
a) 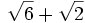
b) 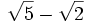
Actividades
Simplifica:
a)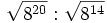
b)![\sqrt[6]{\sqrt{8}}](/wikipedia/images/math/b/d/b/bdbeee310b4a724e942f08bffbfa8d23.png)
c)![\sqrt[9]{12} \cdot \sqrt{3}](/wikipedia/images/math/7/2/8/72833303cca23937986fcffc7c483ab7.png)
Simplifica: 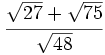
Simplifica: ![\sqrt [4]{\sqrt{x^3} \cdot 16 \sqrt{x}}](/wikipedia/images/math/c/b/1/cb16004d071779fc6b1ffc6f93945a68.png)
Simplifica: ![\left(\cfrac{\sqrt [6]{32}}{\sqrt{8}} \right)^3](/wikipedia/images/math/e/a/c/eacfafeb055cc8c9cdb0aad1d2009d5a.png)
Simplifica (Extracción e introducción de factores en un radical):
a) ![\sqrt[3]{5^{17} \cdot 4^6}](/wikipedia/images/math/0/0/5/005d7f0a77ef68096dbc57b6faf62174.png)
b) ![\sqrt[3]{16\, a^4\, b^{21}}](/wikipedia/images/math/1/0/a/10a9ce8e21e1692804f04887051c25a2.png)
c) ![7^3 \cdot 6^9 \sqrt[11]{y^3}](/wikipedia/images/math/6/d/d/6dd037766dcba2853e802af0eb172662.png)
Simplifica:
a) 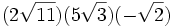
b) ![(5\sqrt[3]{4})(2\sqrt[3]{2})](/wikipedia/images/math/c/4/a/c4a86a9d45d3ab1a13edab27c030aed9.png)
c) ![(7\sqrt{2})(5\sqrt[3]{3})](/wikipedia/images/math/9/8/1/981355fbebaebcc7ed55c7fad7b969d5.png)
Simplifica:
a) 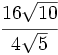
b) ![\cfrac{24\sqrt[4]{2}}{4\sqrt[5]{3}}](/wikipedia/images/math/b/3/c/b3c493d2101ba7fdd69acb88e870ea21.png)
Simplifica:
a) 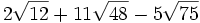
b) 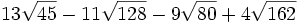
Simplifica:
a) ![3\sqrt[5]{2}+7\sqrt[5]{2}](/wikipedia/images/math/d/2/7/d27d96074bab9896a713780d59467405.png)
b) 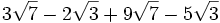
c) ![3\sqrt[3]{54}-2\sqrt[3]{2}+9\sqrt[3]{16}](/wikipedia/images/math/1/d/0/1d09e34f1f3456a7a3bee748760e4d4f.png)
d) ![4\sqrt[4]{25}-\sqrt{45}](/wikipedia/images/math/d/d/b/ddb97312176c5bcecf2ee242e8ad1131.png)
e) ![\cfrac{1}{2}\sqrt[3]{108}-\cfrac{3}{2}\sqrt[3]{4}](/wikipedia/images/math/b/d/5/bd562c177c7713390d93927f9b4bc7d4.png)
Calcula y simplifica:
- a)
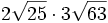 ; b)
; b) 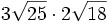 ; c)
; c) 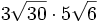
- d)
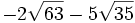 ; e)
; e) 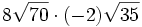 ; f)
; f) 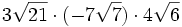
- g)
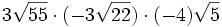 ; f)
; f) 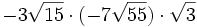
Opera y simplifica:
- a)
![2\sqrt[3]{18} \cdot 3\sqrt[3]{12}\;](/wikipedia/images/math/0/3/1/031733f0fbd54f968faa9fe5eda8d0a5.png) ; b)
; b) ![3\sqrt[3]{50} \cdot 2\sqrt[3]{20}\;](/wikipedia/images/math/5/3/2/5325b2d9d555d9f858cb45e672a5d4f1.png) ; c)
; c) ![3\sqrt[3]{45} \cdot 5\sqrt[3]{75}\;](/wikipedia/images/math/d/0/3/d03eb8f8d36666972cc949f4aa84135f.png)
- d)
![-2\sqrt[3]{28} \cdot 5\sqrt[3]{98}\;](/wikipedia/images/math/a/e/0/ae069089d23479aab015b6e60f86d52f.png) ; e)
; e) ![8\sqrt[3]{-12} \cdot (-3\sqrt[3]{3}) \cdot \sqrt[3]{-6}\;](/wikipedia/images/math/4/c/2/4c2775ca1af101fe6d39c7594ff03cf3.png) ; f)
; f) ![3\sqrt[3]{8} \cdot (-7\sqrt[3]{9}) \cdot 4\sqrt[3]{3}\;](/wikipedia/images/math/7/6/2/762033e0f8daa6c889ef1b8ff3aedd7a.png)
- g)
![-5\sqrt[3]{27} \cdot (-\sqrt[3]{4}) \cdot 4\sqrt[3]{2}\;](/wikipedia/images/math/c/7/a/c7a78297a356e0f2492f0896287bf16f.png) ; h)
; h) ![3\sqrt[3]{20} \cdot (-3\sqrt[3]{10}) \cdot (-4\sqrt[3]{5})\;](/wikipedia/images/math/6/6/6/666f233d469263babf8b6568f8816f5f.png) ; i)
; i) ![3\sqrt[6]{324} \cdot 5\sqrt[6]{144}\;](/wikipedia/images/math/d/3/e/d3ec755367d0b6a0b64cb68db1a7cd6d.png)
- j)
![-2\sqrt[4]{250} \cdot 5\sqrt[4]{40}\;](/wikipedia/images/math/4/5/9/45941ba5c1a9b2af7e5f5acfe1ab8614.png) ; k)
; k) ![3\sqrt[4]{88} \cdot (-7\sqrt[8]{216}) \cdot 4\sqrt[8]{162}\;](/wikipedia/images/math/4/8/6/48604a9cfa646b3261cb09804c4afc34.png)
Opera y simplifica:
- a)
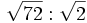 ; b)
; b) 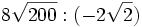
Opera y simplifica:
- a)
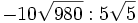 ; b)
; b) 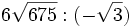 c)
c) 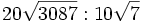
- d)
![9\sqrt[3]{432} : (-\sqrt[3]{-2})\;](/wikipedia/images/math/f/b/9/fb95dd8cbe8cfd4e0c49eec43dda6ff7.png) ; e)
; e) ![-10\sqrt[3]{1458} : 5\sqrt[3]{2}\;](/wikipedia/images/math/e/e/f/eef5a8ba7329df0a841ecd829db26562.png) ; f)
; f) ![12\sqrt[3]{192} : (-6\sqrt[3]{-3})\;](/wikipedia/images/math/8/0/7/807881bc4d10def8325191dac48379b0.png)
- g)
![-30\sqrt[3]{3000} : 6\sqrt[3]{3}\;](/wikipedia/images/math/f/f/e/ffec5e6b75ac1f80c24af9caa431a158.png) ; h)
; h) ![\sqrt[4]{512} : \sqrt[4]{2}\;](/wikipedia/images/math/0/b/5/0b5ce95019fc14a1775557e6ba43ac1b.png) ; i)
; i) ![9\sqrt[4]{768} : (-\sqrt[4]{3})\;](/wikipedia/images/math/0/6/5/06566e947dc6e1be1bb70ce72612c1b0.png)
- j)
![-10\sqrt[4]{2592} : 5\sqrt[4]{2}\;](/wikipedia/images/math/5/9/c/59c73064c6c6c8edd9a75643e619e889.png) ; k)
; k) ![12\sqrt[4]{3888} : (-6\sqrt[4]{3})\;](/wikipedia/images/math/e/6/f/e6f826708d9b60ae3eec0ce03419beaa.png) ; l)
; l) ![-30\sqrt[4]{13122} : 6\sqrt[4]{2}\;](/wikipedia/images/math/f/3/8/f38325af6ab9a4b792be123712a935eb.png)
Calcula:
- a)
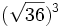 ; b)
; b) 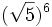 ; c)
; c) 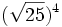 ; d)
; d) 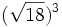
Calcula:
- a)
![(\sqrt[3]{-100})^4\;](/wikipedia/images/math/f/9/8/f9898c4fea7d81c6a960d595902aed45.png) ; b)
; b) ![(\sqrt[3]{18})^4\;](/wikipedia/images/math/b/8/2/b821a9571353a23729e0d70db373b576.png) ; c)
; c) ![(\sqrt[4]{7})^5\;](/wikipedia/images/math/7/e/5/7e5c3062446a9e6e968bcc8e047c05f2.png) ; d)
; d) ![(\sqrt[4]{21})^7\;](/wikipedia/images/math/d/2/2/d2219bd465cdf2cd6bd4ee043a87fa68.png)
- e)
![(\sqrt[4]{100})^5\;](/wikipedia/images/math/d/e/e/dee501759eec044d5e4b65b67661a26a.png) ; f)
; f) ![(\sqrt[5]{16})^7\;](/wikipedia/images/math/c/4/7/c477f227f0e345150bd5d4465006a35c.png) ; g)
; g) ![(\sqrt[6]{12})^7\;](/wikipedia/images/math/a/f/f/aff12187841d83e96f42fc74b7813d9e.png)
Calcula y simplifica:
- a)
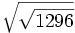 ; b)
; b) 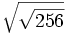 ; c)
; c) ![\sqrt[3]{\sqrt{46\,656}}\;](/wikipedia/images/math/4/4/b/44b6d41e62a3bb8b4f098b0be493b394.png)
- d)
![\sqrt[3]{\sqrt[3]{4096}}\;](/wikipedia/images/math/b/a/5/ba5c5b911a2c67423eff1042451512d8.png) ; e)
; e) ![\sqrt{\sqrt[3]{1024}}\;](/wikipedia/images/math/0/d/f/0df78f26900c5ba4320ea30e1acdadc1.png) ; f)
; f) ![\sqrt[4]{\sqrt[3]{4096}}\;](/wikipedia/images/math/4/3/8/4388e0aec792ebc9974cea4ab170a49d.png)
En esta escena podrás practicar la suma y resta de radicales con o sin el mismo índice.
Ejercicios de autoevaluación sobre sumas y restas de radicales.
Ejercicios de autoevaluación sobre raíces de radicales.
Racionalización de denominadores
Se llama racionalización al procedimiento por el cual a partir de una fracción con raíces en el denominador obtenemos otra fracción equivalente sin raíces en el denominador.
Los dos videotutoriales siguientes resumen lo que vamos a ver en este apartado:
Tutorial en el que se explica y trabaja la racionalización de quebrados con radicales, en el caso en que el denominador es un monomio, es decir, un único término.
- 00:00 a 02:50: Explicación del proceso de racionalización.
- 02:50 a 09:50: Ejemplos donde se analizan los errores más típicos cometidos en la racionalización con un monomio en el denominador.
- 09:50 a 17:18: Ejercicios de racionalización con monomios en el denominador.
Tutorial en el que se explica y trabaja la racionalización de quebrados con radicales, en el caso en que el denominador es un binomio, es decir, suma de dos términos.
- 00:00 a 01:30: Explicación del proceso de racionalización.
- 01:30 a 09:40: Ejemplo donde se analizan los errores más típicos cometidos en la racionalización con un binomio en el denominador.
- 09:40 a 13:35: Ejercicios de racionalización con binomios en el denominador.
- 13:35 a 17:14: Ejercicio de racionalización con un trinomio en el denominador.
Qué es racionalizar y cómo resolver los diferentes casos.
Cómo se racionalizan los denominadores de las fracciones. Ejemplos.
Caso 1: Denominador con raíces cuadradas
Procedimiento
Para racionalizar una fracción con una raíz cuadrada en el denominador se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma.
Ejemplo: Caso 1: Denominador con raíces cuadradas
Racionalizar 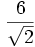
En este caso hay que multiplicar numerador y denominador por 
Racionaliza: 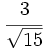 .
.
Racionaliza: 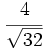 .
.
Racionaliza: 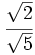 .
.
Racionaliza: 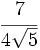 .
.
Racionaliza: 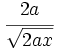 .
.
Caso 2: Denominador con otras raíces
Procedimiento
Para racionalizar una fracción con una raíz de índice distinto de dos en el denominador, se deben multiplicar el numerador y denominador de la fracción por una raíz con el mismo índice en la que cada exponente de los factores del radicando se calculará como:
- La diferencia entre el índice del radical y el exponente actual, caso de que el índice sea mayor o igual que el exponente actual.
- La diferencia entre el exponente actual y el múltiplo del indice más cercano a dicho exponente, caso de que el exponente actual supere al índice.
Ejemplo: Caso 2: Denominador con otras raíces
Racionalizar ![\frac{{2}}{\sqrt[5]{a^3b^4}}](/wikipedia/images/math/5/3/3/533185378740f77c6d3da802a18e1fdd.png)
En este ejemplo, hay que multiplicar numerador y denominador por ![\sqrt[5] {a^2b}](/wikipedia/images/math/3/d/5/3d57844c30135fee650c9bcfd98d40d1.png) , ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz:
, ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz:
Racionaliza: ![\cfrac{2}{\sqrt[4]{3}}](/wikipedia/images/math/3/6/3/363cdd6889755a849dc9a7ea0bac576d.png) .
.
Racionaliza: ![\cfrac{1}{\sqrt[5]{8}}](/wikipedia/images/math/b/a/0/ba08551ff4220087d9fbb68dee2ffd73.png) .
.
Racionaliza: ![\cfrac{5}{2\,\sqrt[3]{7}}](/wikipedia/images/math/8/3/b/83b21b3caaf20fd75d0e6b3f0a3cc8c3.png) .
.
Racionaliza: ![\cfrac{4}{\sqrt[5]{72}}](/wikipedia/images/math/6/b/b/6bb931ba83b1b6b45859a0561fd025ca.png) .
.
Racionaliza: ![\cfrac{6}{5\sqrt[3]{3x}}](/wikipedia/images/math/d/e/5/de5a661d559994439a2bc7870429d027.png) .
.
Racionaliza: ![\cfrac{9}{5\sqrt[4]{27x^2}}](/wikipedia/images/math/7/8/2/7822ef646d2405a4313f31ef0d3bfa53.png) .
.
Caso 3: Denominador con sumas y restas de raíces cuadradas
Procedimiento
Para racionalizar fracciones en cuyo denominador aparezcan binomios con alguna raíz cuadrada, se multiplica y divide por la expresión conjugada del denominador, esto es, por la misma expresión en la que solo se le cambia el signo del segundo término del binomio.
Ejemplo: Caso 3: Denominador con sumas y restas de raíces
Racionalizar 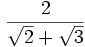
En este caso hay que multiplicar el numerador y el denominador por 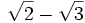 (este resultado es el que da el producto notable de los binomios conjugados):
(este resultado es el que da el producto notable de los binomios conjugados):
Racionaliza: 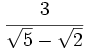 .
.
Racionaliza: 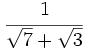 .
.
Racionaliza: 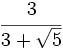 .
.
Racionaliza: 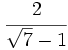 .
.
Racionaliza: 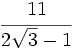 .
.
Racionaliza: 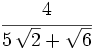 .
.
Racionaliza: 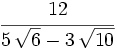 .
.
Racionaliza: 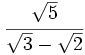 .
.
Racionaliza: 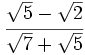 .
.
Racionaliza: 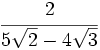 .
.
Racionaliza: 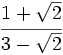 .
.
Racionaliza: 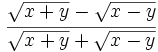 .
.
Caso 4: Denominador con sumas y restas de raíces cúbicas (Avanzado)
Para este caso deberás conocer primero las siguientes identidades de la suma y diferencia de cubos:
Demostración y ejemplos de las identidades:
- Suma de cubos:
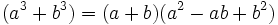
- Diferencia de cubos:
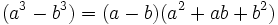
Racionaliza: ![\cfrac{1}{\sqrt[3]{9}+\sqrt[3]{2}}](/wikipedia/images/math/5/2/5/525844969b81af2a18046b55c583cf16.png) .
.
Racionaliza: ![\cfrac{2}{\sqrt[3]{7}-\sqrt[3]{3}}](/wikipedia/images/math/2/5/b/25b5b6bd40a7dd60bcdc8736b47d38e9.png) .
.
Racionaliza: ![\cfrac{2}{\sqrt[3]{25}+\sqrt[3]{15}+\sqrt[3]{9}}](/wikipedia/images/math/8/6/3/863071bfa12d745b2ba15899c0fb3793.png) .
.
Racionaliza: ![\cfrac{22}{\sqrt[3]{25}-\sqrt[3]{5}+1}](/wikipedia/images/math/c/e/1/ce1cad8992e279a2b317175de6241c79.png) .
.
Actividades
Racionaliza:
a)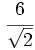 b)
b) ![\cfrac{6}{\sqrt[5]{2^2}}\;](/wikipedia/images/math/4/5/3/45300658ad66f636e45d5a937abb9ce2.png) c)
c) 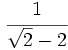 d)
d) 
Racionaliza:
a)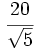 b)
b) ![\cfrac{16}{\sqrt[3]{2}}\;](/wikipedia/images/math/d/c/e/dce724def14d2562ee1fd77bf2833432.png) c)
c) ![\cfrac{22}{3\,\sqrt[5]{4}}\;](/wikipedia/images/math/2/b/0/2b086052936cad993cb0c4a22d48db74.png)
Racionaliza: ![\cfrac{3ab}{\sqrt[4]{a^2b^3c}}\;](/wikipedia/images/math/7/0/9/709ab631d1a8344d94c8314001dfa88f.png)
Racionaliza: 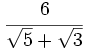
Simplifica: ![\cfrac{\sqrt[4]{a^3} \cdot a^{-1}}{a\,\sqrt{a}}\;](/wikipedia/images/math/d/c/4/dc4044e264b4425b4d26164a0f610b4d.png)
Racionaliza: 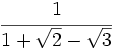
Racionaliza:
a) 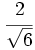 b)
b) ![\cfrac{4}{\sqrt[3]{5}}](/wikipedia/images/math/5/5/a/55ace2b51fb5fc69060e01f2b64ae22a.png) c)
c) ![\cfrac{3}{\sqrt[4]{729}}](/wikipedia/images/math/4/4/1/4414906695a164be992fb3ccd577a118.png) d)
d) ![\cfrac{5}{\sqrt[5]{125}}](/wikipedia/images/math/c/5/f/c5ffa5189009ca20a4f17a6a26380002.png)
Racionaliza:
a) 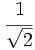 b)
b) 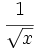 c)
c) 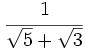 d)
d) 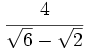 e)
e) ![\cfrac{1}{\sqrt[3]{2}}](/wikipedia/images/math/d/e/9/de9cd45023621984a57f028dd79d3f13.png) f)
f) ![\cfrac{1}{\sqrt[4]{8}}](/wikipedia/images/math/3/c/7/3c78c7350c28bda84045acdb35b5491a.png)
Racionaliza:
- 68)
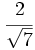 69)
69) 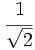 70)
70) 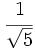 71)
71) 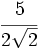
- 72)
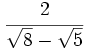 73)
73) 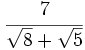 74)
74) 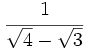
Racionaliza:
- 75)
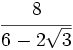 76)
76) 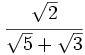 77)
77) 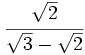
- 78)
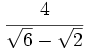 79)
79) 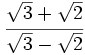 80)
80) 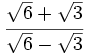
Actividades en las que podrás aprender a racionalizar denominadores
Ejercicios de autoevaluación sobre racionalización.
Ejercicios propuestos
|
Ejercicios propuestos: Radicales |
![\sqrt[5]{32}=2\;](/wikipedia/images/math/e/f/a/efae07f29bbbaaef03acb5b46afffb59.png) porque
porque 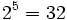 .
.
![\sqrt[3]{1}=1](/wikipedia/images/math/d/5/3/d53d30c7123945d21786c0fb38eeeb18.png) .
.
![\sqrt[5]{0}=0](/wikipedia/images/math/e/9/5/e95b8cee4e9e352608032036b0bd68d7.png) .
.
![\sqrt[4]{16}=\pm 2](/wikipedia/images/math/3/5/c/35cc75069a6350b569ad8c8f72bf6ae2.png) porque
porque 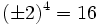 .
.
![\sqrt[3]{64}=4](/wikipedia/images/math/f/2/4/f2482a82a1ce97518a3bbef09d9575b5.png) porque
porque 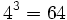 .
.
![\sqrt[3]{-8}=-2](/wikipedia/images/math/1/5/4/154ab22db729e6b6490caa36d8669830.png) porque
porque 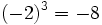 .
.
![\sqrt[4]{-8}= no \ existe](/wikipedia/images/math/a/2/1/a21d3d89fedd78f5c9a6378b3cf240f3.png) porque ningún número elevado a 4 puede dar negativo (-8).
porque ningún número elevado a 4 puede dar negativo (-8).
![\sqrt[n]{a^m}=a^\frac{m}{n}](/wikipedia/images/math/3/b/0/3b0234682d54453ceee722e89c782c2e.png)
![a)\ \sqrt[3] {125^4} \quad b)\ \sqrt {100^{-3}}](/wikipedia/images/math/5/9/e/59ebdba87736732560d47ebf9c21a75e.png)
![3^a=\sqrt[5]{3^2}](/wikipedia/images/math/6/d/8/6d842078dcc499bd8f7362de399b3095.png)
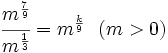
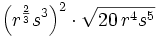
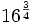
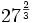
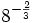
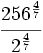
![6^{\frac{1}{2}} \cdot \left(\sqrt[5]{6}\right)^3](/wikipedia/images/math/6/5/e/65e6f10ec848c362c461db20665256a8.png)
![a) \sqrt[3]{216} \quad b) \sqrt[4]{0.0256}\quad c) \sqrt[3]{192}](/wikipedia/images/math/d/f/7/df7f4bb983c565de5f6c5ab3ff89efdd.png)
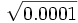
![\sqrt[3] {-512}](/wikipedia/images/math/d/5/0/d5007990ae7e9a5dddf6e4eff90d9a71.png)
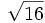
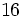
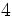
![\sqrt [3] {8}](/wikipedia/images/math/f/5/2/f5234f8dd97fefc954cf62fa258a3b72.png)
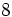

![\sqrt [4]{81}](/wikipedia/images/math/e/c/6/ec6e7957bf989cbaf4c80a2e4c59755c.png)
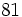

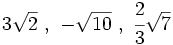
![3\sqrt[3]{2} \ , \ -\sqrt[3]{2} \ , \ \cfrac{2}{3}\sqrt[3]{2}](/wikipedia/images/math/1/1/c/11ca38664b260e771d7b6b60dd01d52b.png)
![\sqrt[n]{a^m}= a^{\frac{m}{n}} \begin{matrix} ~_{(1)}~ \\ = \\ \, \end{matrix} a^{c+\frac{r}{n}}= a^c \cdot a^{\frac{r}{n}}= a^c \cdot \sqrt[n]{a^r}](/wikipedia/images/math/d/3/9/d39083130ff7fc81f2df907b77c139e4.png)
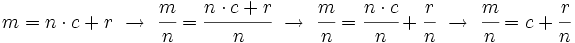
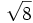 b)
b) 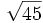
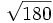
![\sqrt[3]{16}\;](/wikipedia/images/math/5/3/a/53a3c4a84f10981709eb9cbe55fd96d6.png) b)
b) ![\sqrt[3]{72}\;](/wikipedia/images/math/7/3/2/73202ad33b01491941443d47216fb27f.png)
![\sqrt[5]{96}\;](/wikipedia/images/math/9/d/c/9dcae009beea43dfbe3404b5f004cc4a.png) b)
b) ![\sqrt[4]{405}\;](/wikipedia/images/math/a/8/9/a890f47fe2c93a2f06c95c8202cb8251.png)
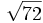 b)
b) ![\sqrt[4]{3645}\;](/wikipedia/images/math/6/4/e/64e81b0470d1d706dc6259ee3c15b821.png) c)
c) 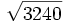 c)
c) ![5\,\sqrt[3]{384}\;](/wikipedia/images/math/4/9/0/4905ec017f8b5e0d98f7ee1f7eec1207.png)
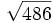 b)
b) ![6\sqrt[3]{1250}\;](/wikipedia/images/math/4/3/4/4346e96a7c5105fca5f88837843083a9.png) c)
c) ![m^3n\sqrt[5]{m^{20}n^{37}}\;](/wikipedia/images/math/4/9/6/496807e951625205ca38c068a23ebc66.png)
![-2\sqrt [3]{16x^5yz^9}](/wikipedia/images/math/5/d/a/5da6c4122805a4279103f0cf5cfb13c0.png)
![\sqrt [4]{32x^4y^{21}z^{43}}](/wikipedia/images/math/c/4/f/c4f4294a30ee9a53a181d8f3abd8d54b.png)
![\sqrt [5]{32x^5y^{-10}z^{-35}}](/wikipedia/images/math/e/f/b/efb9fab775fddc918c97f70c90e23eb4.png)
![\sqrt [5]{-243a^{20}}](/wikipedia/images/math/e/e/3/ee38623c8fe3fac34be9faf93f9e8457.png)
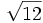 ; b)
; b) 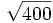 ;
;
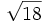 ; e)
; e) 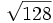
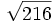 ; g)
; g) 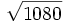 ; h)
; h) ![\sqrt[3]{625}\;](/wikipedia/images/math/e/5/d/e5d68b00dfbd79e2f3d58e0aca3d7c0f.png)
![\sqrt[3]{432}\;](/wikipedia/images/math/6/d/1/6d13f38f4d1eb2019980f043401b4212.png) ; j)
; j) ![\sqrt[3]{-216}\;](/wikipedia/images/math/f/2/e/f2e9196b5535a696cacaea492b5fca1f.png) ; k)
; k) ![\sqrt[3]{243}\;](/wikipedia/images/math/8/f/5/8f5ffd08c6adee125672bdaceac21095.png)
![\sqrt[4]{1296}\;](/wikipedia/images/math/d/f/8/df8a4653fd51d5f3a467722317d864f7.png) ; m)
; m) ![\sqrt[4]{20736}\;](/wikipedia/images/math/e/0/3/e0364ebd0e97bb3e82e855e75e9794bd.png) ; n)
; n) ![\sqrt[5]{-480}\;](/wikipedia/images/math/f/5/e/f5e99ceeb09f023ea88f8aae9d707acc.png)
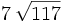
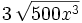
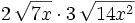
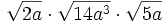
![5\,\sqrt[3]{2x^2} \cdot 3\,\sqrt[3]{4x^4}\;](/wikipedia/images/math/b/4/5/b4564f0c1cace422e46c7b4e8bef605e.png)
![\sqrt[3]{125x^6y^3}](/wikipedia/images/math/6/4/b/64b184793ed736d13012a61c0bb6a166.png)
![\sqrt[4]{5a^4b^{12}}](/wikipedia/images/math/a/b/a/abab543450564364e8ced43319182eb4.png)
![a \sqrt[n]{b}=a \cdot b^{\frac{1}{n}}=(a^n)^{\frac{1}{n}} \cdot b^{\frac{1}{n}}= (a^n \cdot b)^{\frac{1}{n}}= \sqrt[n]{a^n \cdot b}](/wikipedia/images/math/7/9/3/793321a371ba1c1c188fd5e877399640.png)
![\sqrt[4]{3} - \sqrt[4]{243}](/wikipedia/images/math/e/6/6/e66fc6d8653c96dff0e3c0b95dc93b55.png)
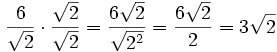
![\frac{{2}}{\sqrt[5]{a^3b^4}} \cdot \frac{\sqrt[5] {a^2b} }{\sqrt[5]{a^2b}} = \frac{{2\sqrt[5]{a^2b}}}{\sqrt[5]{a^5b^5}} = \frac{{2\sqrt[5]{a^2b}}}{{ab}}](/wikipedia/images/math/0/a/6/0a6d73fa5ee1fe441c50539e138ae167.png)