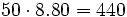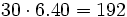Problemas clásicos (3ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 47)
Repartos proporcionales
En los repartos proporcionales tenemos que repartir una cantidad en varias partes, de manera que cada parte sea proporcional a cada fracción en que se parte el total.
Ejercicio resuelto: Repartos proporcionales
Tres grifos aportan 2 l/s, 5 l/s y 7l/s, respectivamente. Se abren los tres simultaneamente para llenar una balsa de 17080 l. Cuando la balsa está llena, ¿qué volumen de agua habrá manado de cada grifo?
Los tres grifos aportan 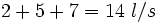 , de manera que:
, de manera que:
El primero aporta 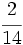 del total
del total 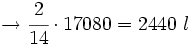
El segundo aporta 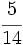 del total
del total 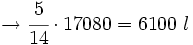
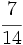 del total
del total 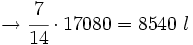
|
Ejercicios propuestos: Repartos proporcionales |
(Pág. 48)
Mezclas
Ejercicio resuelto: Mezclas
- Se muelen conjuntamente 50 kg de café de 8.80 €/kg y 30 kg de otro café de inferior calidad, de 6.40 €/kg. ¿A cómo resulta el kilo de la mezcla obtenida?
Para resolverlo haremos uso de la siguiente tabla:
| Precio de la mezcla = 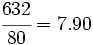 € €
|
|
Ejercicios propuestos: Mezclas |
(Pág. 49)
Móviles
A tener en cuenta ...
- Dos móviles que van uno al encuentro del otro, se aproximan con una velocidad relativa igual a la suma de las velocidades absolutas de cada móvil.
- Dos móviles que van uno en persecusión del otro, se aproximan con una velocidad relativa igual a la diferencia de las velocidades absolutas de cada móvil.
Ejercicios resueltos: Móviles
- 1. Un ciclista profesional, entrenándose, avanza por una carretera a una velocidad de 38 km/h. Más adelante, a 22 km, un cicloturista avanza en el mismo sentido a 14 km/h. ¿Cuánto tarda el ciclista profesional en alcanzar al cicloturista?
- b) Un motorista y un coche avanzan por una carretera, dirigiéndose el uno hacia el otro, a unas velocidades de 50 km/h y 100 km/h, respectivamente. Si los separa una distancia de 10 km, ¿cuánto tiempo tardarán en encontrarse?
- Solución 1:
- Los ciclistas se aproximan a una velocidad de 38 - 14 = 24 km/h.
- Calculamos el tiempo hasta que se encuentran, sabiendo que les separan 22 km:
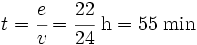
- Solución 2:
- Los dos se aproximan a una velocidad de 50 + 100 = 150 km/h.
- Calculamos el tiempo hasta que se encuentran, sabiendo que les separan 10 km:
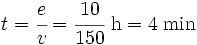
|
Ejercicios propuestos: Móviles |