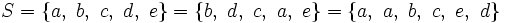Conjuntos
De Wikipedia
Tabla de contenidos |
Los conjuntos son un concepto primitivo, en el sentido de que no es posible definirlos en términos de nociones más elementales, por lo que su estudio puede realizarse de manera informal, apelando a la intuición y a la lógica. Por otro lado, son el concepto fundamental de la matemática: mediante ellos puede formularse el resto de objetos matemáticos, como los números y las funciones, entre otros. Su estudio detallado requiere pues la introducción de axiomas y conduce a la teoría de conjuntos.
Definición y notación
- Un conjunto es una colección bien definida de objetos, entendiendo que dichos objetos pueden ser cualquier cosa: números, personas, letras, otros conjuntos, etc. Los conjuntos se denotan habitualmente por letras mayúsculas. Al definir un conjunto es habitual meter sus elementos entre llaves:
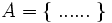
- Relación de pertenecia: Los objetos que componen el conjunto se llaman elementosmiembros. Un elemento se dice que «pertenece» al conjunto y se denota mediante el símbolo
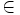 , si forma parte de él. Este símbolo lo introdujo Peano. La expresión
, si forma parte de él. Este símbolo lo introdujo Peano. La expresión 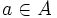 se lee «a pertenece a A». Para la noción contraria se usa el símbolo
se lee «a pertenece a A». Para la noción contraria se usa el símbolo 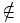 .
.
- Formas de definir un conjunto:
- Por comprensión: mediante una propiedad que todos sus elementos poseen.
- Por extensión: mediante la lista de todos sus elementos.
- Si para los números naturales se considera la propiedad de "ser un número natural menor que 5", entonces, el conjunto de los números naturales menores que 5 sería:
- Por extensión:
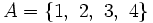
- Por comprensión:
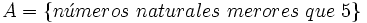 ó
ó 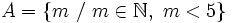
- (En la segunda expresión la barra oblicua "/" significa «tal que». En lugar de la barra oblicua se utiliza también la barra vertical " | " o los dos puntos ":")
- Por extensión:
Igualdad de conjuntos
Un conjunto está definido únicamente por los elementos que lo componen, y no por la manera en la que se lo representa. Por ello, la igualdad de conjuntos se establece como:
Axioma de extensionalidad: Dos conjuntos A y B que tengan los mismos elementos son el mismo conjunto, A=B.
Esta propiedad tiene varias consecuencias.
Consecuencias del axioma de extensionalidad
- Un mismo conjunto puede especificarse de muchas maneras distintas, por extensión o por comprensión, y ser el mismo conjunto.
- El orden en el que se listan los elementos no se tiene en cuenta para comparar dos conjuntos.
- Un conjunto no puede tener elementos «repetidos», ya que un objeto solo puede o bien ser un elemento de dicho conjunto o no serlo. Si en la lista aparece un elemento repetido es como si sólo apareciese una vez.
Conjunto vacío
Plantilla:AP El conjunto que no contiene ningún elemento se llama el conjunto vacío y se denota por Plantilla:Math o simplemente {}. Existe un único conjunto vacío, ya que lo único que distingue a un conjunto son sus elementos.
Subconjuntos
Plantilla:AP [[Archivo:Subset-2.svg|thumb|280px|Subconjunto. Plantilla:Math es un subconjunto de Plantilla:Math (en particular un subconjunto propio).]] Un subconjunto Plantilla:Math de un conjunto Plantilla:Math, es un conjunto que contiene algunos de los elementos de Plantilla:Math (o quizá todos): Plantilla:Definición Cuando Plantilla:Math es un subconjunto de Plantilla:Math, se denota como Plantilla:Math y se dice que «Plantilla:Math está contenido en Plantilla:Math». También puede escribirse Plantilla:Math, y decirse que Plantilla:Math es un superconjunto de Plantilla:Math y también «Plantilla:Math contiene a Plantilla:Math» o «Plantilla:Math incluye a Plantilla:Math».
Todo conjunto Plantilla:Math es un subconjunto de sí mismo, ya que siempre se cumple que «cada elemento de Plantilla:Math es a su vez un elemento de Plantilla:Math». Es habitual establecer una distinción más fina mediante el concepto de subconjunto propio: Plantilla:Math es un subconjunto propio de Plantilla:Math si es un subconjunto de Plantilla:Math pero no es igual a Plantilla:Math. Se denota como Plantilla:Math, es decir: Plantilla:Math pero Plantilla:Math (y equivalentemente, para un superconjunto propio, Plantilla:Math).<ref group="n">También se utiliza la notación Plantilla:Math y Plantilla:Math, pero según el autor esto puede denotar subconjunto, Plantilla:Math y Plantilla:Math; o subconjunto propio, Plantilla:Math y Plantilla:Math. Véase Subconjunto.</ref>
Ejemplos.
- El «conjunto de todos los hombres» es un subconjunto propio del «conjunto de todas las personas».
- Plantilla:Math}
- Plantilla:Math}
Conjuntos disjuntos
Plantilla:Ap Dos conjuntos Plantilla:Math y Plantilla:Math son disjuntos si no tienen ningún elemento en común. Por ejemplo, los conjuntos de los números racionales y los números irracionales son disjuntos: no hay ningún número que sea a la vez racional e irracional. La intersección de dos conjuntos disjuntos es el conjunto vacío.