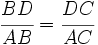Semejanza de triángulos (3ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 186)
Triángulos semejantes
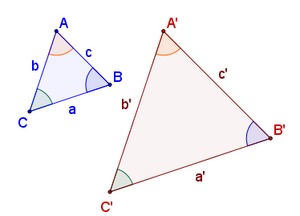
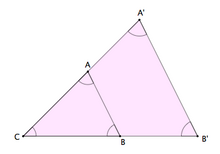
Se dice que dos figuras geométricas, y en particular dos triángulos, son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes.
Matemáticamente, la semejanza de triángulos la podemos expresar de la siguiente manera:
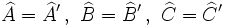
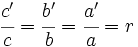
|
(*) Dos elementos de dos figuras son homólogos si ocupan el mismo lugar en ambas figuras.
Nota: Cuando veamos los criterios de semejanza de triángulos, veremos que para que dos triángulos sean semejantes bastará con que se cumpla una de las dos condiciones: que los lados homólogos sean proporcionales o que los ángulos homólogos sean iguales. En tal caso, la otra condición se cumplirá automáticamente.
En este video exploraremos el comportamiento del área respecto a la longitud de los lados de un triángulo equilátero.
Criterios de semejanza de triángulos
Los criterios de semejanza de triángulos simplifican el número de condiciones que deben comprobarse para que dos triángulos sean semejantes:
Criterios de semejanza de triángulos
- Dos triángulos son semejantes si tienen los lados proporcionales:
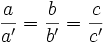
- Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales:
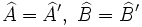
- Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo comprendido:
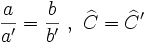
Actividades para aprender y practicar los criterios de semejanza de triángulos.
Tutorial en el que se explica y trabaja los criterios de semejanza de triángulos y se resuelven algunos ejercicios sencillos en los que se aplican dichas propiedades.
- 00:00 a 06:08: Criterios de Igualdad (Congruencia) de Triángulos.
- 06:08 a 08:30: Definición de Triángulos Semejantes.
- 08:30 a 15:30: 1er criterio de semejanza, lados proporcionales.
- 11:00 - Ejemplo del 1er criterio de semejanza.
- 15:30 a 21:30: 2º criterio de semejanza, ángulos iguales.
- 17:00 - Ejemplo del 2º criterio de semejanza.
- 21:30 a 26:30: 3er criterio de semejanza, ángulo igual y sus lados proporcionales.
- 23:05 - Ejemplo del 3er criterio de semejanza.
- 26:30 a 32:54 : Ejercicio donde se aplica la semejaza de triángulos.
Ejemplos de aplicación de los criterios de semejanza.
Los lados de un triángulo miden 3, 4 y 6 cm, y los lados de otro triángulo miden 9,12 y 18 cm. Comprueba si son semejantes.
Dos ángulos de un triángulo miden 55º y 85º, y dos de los ángulos de otro triángulo miden 55º y 65º. ¿Son semejantes?.
Cálculo altura inaccesible usando dos triángulos semejantes
En esta escena podrás ver los tres criterios de semejanza de triángulos.
Aplicaciones de los criterios de semejanza
Los criterios de semejanza que hemos visto tienen numerosas aplicaciones. Veamos algunas de ellas.
Ejercicios de aplicación de los criterios de semejanza de triángulos:
- Medición de alturas con sombras.
- Medición de alturas con espejos.
- ¿Cómo pudo medir Tales la altura de una pirámide?
En esta escena podrás hallar la altura de una casa utilizando un espejo y una cinta métrica.
Cuenta la historia que un sacerdote egipcio le preguntó a Tales de Mileto (s. IV a. C) acerca de la altura de la Pirámide de Keops, cuando ya las pirámides rondaban los 2.000 años de edad, y éste respondió con un método de lo más ingenioso para medir dicha altura..
Aplicación del teorema de la bisectriz.
Problema:
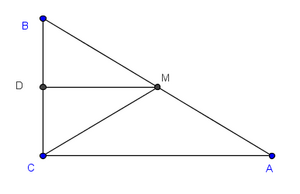
En un triángulo ABC se traza la mediana CM y desde A se traza el segmento AN que corta a la mediana CM en su punto medio T. Sabiendo que TN = 5 cm, calcula el valor de AT.
Solución:
Véase el video para ver la solución.
Demostración:
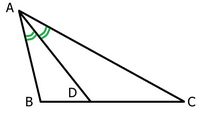
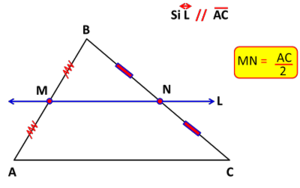
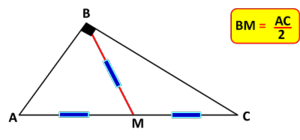
Los triángulos ABC y MBN son semejantes por estar en la posición de Tales. Además la razón de semejanza es claramente 2, por lo que lo que se nos pide es bastante inmediato.
| Problema:
Halla el valor de "x" en la figura:
Solución: Véase el video para ver la solución. | 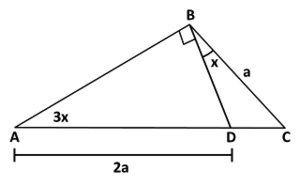
|
Teorema de Tales
Primer teorema de Tales
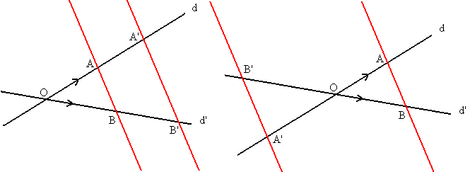
| Dos rectas paralelas, AB y A'B', que cortan a dos rectas secantes, d y d', determinan en éstas segmentos proporcionales:
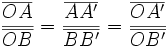 |
Demostración del primer teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
En esta escena podrás comprobar el primer teorema de Tales.
Triángulos en la posición de Tales
Dos triángulos ABC y A'B'C', con sus lados paralelos y encajados con un vértice común, se dice que están en la posición de Tales Teorema de Tales. Ejemplos. Tutorial en el que se explica y trabaja el teorema de Tales y se resuelven algunos ejercicios sencillos en los que se aplican dichas propiedades.
División de un segmento en partes proporcionales. Dibujo y cálculo del 4º proporcional a tres segmentos dados. Cálculo y dibujo del 3º proporcional a dos segmentos dados. Ejercicio de aplicación del primer teorema de Tales. Ejercicio de aplicación del primer teorema de Thales. Otra forma equivalente de enunciar el teorema de Tales utilizando la semejanza de triángulos: Dos triángulos encajados (en la posición de Tales) son semejantes y en consecuencia sus lados son proporcionales. Ejemplo de aplicación del teorema de Tales. Ejemplo de aplicación del teorema de Tales. Ejemplo de aplicación del teorema de Tales. Ejemplo de aplicación del teorema de Tales. Ejemplo de aplicación del teorema de Tales. Ejemplo de aplicación del teorema de Tales. |
Apéndice
Polígonos semejantes
Dos polígonos son semejantes si cumplen que sus ángulos homólogos son iguales y sus lados homólogos son proporcionales.
Propiedades
Si dos polígonos son semejantes y k es la constante de proporcionalidad, entonces:
- La razón entre sus perímetros también es k.
- La razón entre sus áreas es k2.
Observa los dos polígonos de la figura. Se dice que son semejantes porque cumplen las dos condiciones antes mencionadas:
- Los ángulos correspondientes son todos iguales.
- Los segmentos correspondientes son proporcionales.
En efecto,
1. Los ángulos son iguales ya que los lados correspondientes son paralelos.
2. Para comprobar que los lados son proporcionales usa los segmentos MN y XY que puedes mover libremente. Mide con ellos dos segmentos correspondientes AB y A'B' por ejemplo y calcula la razón de semejanza.
Mueve ahora el punto rojo para comprobar el valor de r.
Polígonos semejantes. Razón de los perímetros y de las áreas.
La razón entre dos cuadrados semejantes es 3/4. Calcula cuánto miden los lados del segundo sabiendo que los del primero miden 24 cm. Calcula el área del primero si la del segundo es 1024 cm2.
Figuras semejantes. Escalas
- De manera intuitiva, dos figuras son semejantes si tienen la misma forma, pero el tamaño es diferente.
- Matematicamente, dos figuras son semejantes si cumplen:
- Los ángulos correspondientes son iguales (misma forma).
- Los segmentos correspondientes son proporcionales.
- Se llama razón de semejanza o escala,
 , al cociente entre dos longitudes correspondientes.
, al cociente entre dos longitudes correspondientes.
Escala y razón de semejanza significan lo mismo. Sin embargo, el término escala suele utilizarse a la hora de confeccionar planos o mapas.
Así, por ejemplo, decimos que un plano está a escala 1:100 si 1 cm en el plano son 100 cm en la realidad. Es lo mismo que decir que la razón de semejanza entre la figura dibujada y la real es 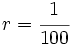 .
.
En una fotografía, la imagen de un persona mide 12 cm, ¿qué escala se ha utilizado si la persona mide en realidad 1.80 m?.
Los planos de un juguete están a escala 1:10. ¿Cuál es la longitud del juguete si en el plano mide 8 cm?.
Ejercicios propuestos
|
Ejercicios propuestos: Semejanza de triángulos |