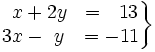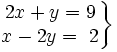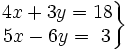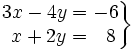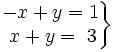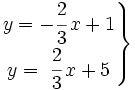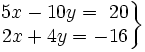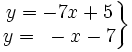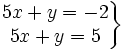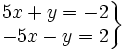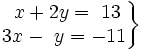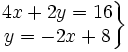Sistemas de ecuaciones lineales (2º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Introducción
Los siguientes videotutoriales resumen gran parte de los conceptos que vamos a ver en esta página:
Tutorial en el que se dan los conceptos básicos respecto a las ecuaciones y sistemas de ecuaciones.
- 00:00 a 01:40: Definición de expresión algebraica.
- 01:40 a 04:00: Definición y ejemplos de ecuaciones.
- 04:00 a 08:32: Definición y ejemplo de solución de una ecuación.
- 08:32 a 10:02: Definición de tipos de igualdades según sus soluciones.
- 10:02 a 10:48: Definición y ejemplos de sistemas de ecuaciones.
- 10:48 a 14:20: Definición y ejemplo de solución de un sistema de ecuaciones.
- 14:20 a Fin: Definición de tipos de sistema de ecuaciones según sus soluciones.
- Definición de sistema de dos ecuaciones lineales con dos incógnitas.
- Sistemas equivalentes.
- Clasificación de los sistemas atendiendo al número de soluciones.
Videotutorial
(Pág. 162)
Sistemas de ecuaciones lineales 2x2
- Un sistema de dos ecuaciones de primer grado con dos incógnitas o simplemente, sistema 2x2 de ecuaciones lineales, es la agrupación de dos ecuaciones de primer grado con dos incógnitas:
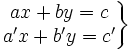
- Se llama solución de un sistema 2x2, a cualquier pareja de valores
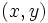 que sea solución de ambas ecuaciones a la vez. Las soluciones de este tipo de sistemas son los puntos de corte de las rectas que representan cada una de las ecuaciones del sistema.
que sea solución de ambas ecuaciones a la vez. Las soluciones de este tipo de sistemas son los puntos de corte de las rectas que representan cada una de las ecuaciones del sistema.
Ejemplo: Solución de un sistema de ecuaciones
Comprueba si las parejas de números (1,2) y (-1,3) son o no soluciones del sistema:
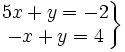
- Para comprobar si (1,2) es solución, sustituimos x=1 e y=2 en las dos ecuaciones del sistema:
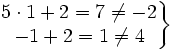
Como no se verifican las dos ecuaciones, la pareja (1,2) no es solución del sistema.
- Para comprobar si (-1,3) es solución, sustituimos x=-1 e y=3 en las dos ecuaciones del sistema:
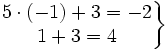
Ejercicios de autoevaluación sobre sistemas de ecuaciones lineales.
Comprueba soluciones de sistemas de ecuaciones lineales.
Método grafico de resolución de sistemas de ecuaciones lineales 2x2
Procedimiento
Para resolver un sistema de ecuaciones lineales, representaremos gráficamente las rectas de las soluciones de cada una de las ecuaciones:
- Si las rectas se cortan, el punto de corte será la única solución del sistema.
- Si las rectas son paralelas, el sistema no tendrá solución.
- Si las rectas son coincidentes, el sistema tendrá infinitas soluciones.
Resolución de sistemas por el método grafico. Ejemplos.
Tutorial en el que se muestra la resolución de sistemas de ecuaciones lineales (grado 1) de dos variables por el método gráfico.
- 00:00 a 01:50: Definiciones iniciales.
- 01:50 a 15:10: Explicación del método gráfico. Ejemplo 1.
- 15:10 a 18:40: Ejemplo 2.
- 18:40 a 22:30: Explicación de los distintos tipos de sistema en función a sus soluciones. Ejemplos 3-4-5.
- 22:30 a Fin: Utilización de la aplicación online DESMOS para la resolución de sistemas de ecuaciones.
Resuelve gráficamente:
Resuelve gráficamente:
Resuelve gráficamente:
Resuelve gráficamente:
Resuelve gráficamente:
1) Resuelve gráficamente:
2) Dada la gráfica (ver video), obtén la solución aproximada del sistema.
3) Resuelve gráficamente:
- Actividad en la que aprenderás a resolver gráficamente un sistema de ecuaciones lineales con dos incógnitas.
- Actividad en la que deberás comprobar si una pareja de números son o no solución de un sistema.
Escena en la que podrás representar graficamente un sistema lineal 2x2 y resolverlo gráficamente.
Resolución de sistemas de ecuaciones por medio de gráficas.
|
Actividad: Método grafico de resolución de sistemas lineales 2x2 Resuelve los siguientes sistemas por el método gráfico:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios propuestos
|
Ejercicios propuestos: Sistemas de ecuaciones lineales |
Número de soluciones de un sistema
Discutir un sistema consiste en decir si el sistema tiene o no tiene solución, y caso de tener, si hay un número finito o infinito de soluciones.
- Un sistema es compatible si tiene solución e incompatible si no la tiene.
- Un sistema es determinado si tiene un número finito de soluciones e indeterminado si tiene infinitas soluciones.
Al discutir un sistema usaremos las siguientes siglas para abreviar:
- S.C.D. : Sistema Compatible Determinado (un número finito de soluciones)
- S.C.I. : Sistema Compatible Indeterminado (infinitas soluciones)
- S.I. : Sistema Incompatible (sin solución)
Discusión de sistemas lineales 2x2
Un sistema 2x2 de ecuaciones lineales puede ser:
- Compatible determinado (S.C.D.): 1 solución
- Compatible indeterminado (S.C.I.): Infinitas soluciones.
- Incompatible (S.I): 0 soluciones.
En efecto, razonando a partir de sus representaciones gráficas:
- Si las dos rectas se cortan en un punto: 1 solución (S.C.D.)
- Si las dos rectas son coincidentes: Infinitas soluciones (S.C.I.)
- Si las rectas son paralelas: 0 soluciones (S.I.)
Averigua si el siguiente sistema es compatible (consistente) o incompatible (inconsistente):
Averigua si el siguiente sistema es compatible determinado o compatible indeterminado:
A partir de la gráfica del video identifica sistemas con o sin solución.
Determina el número de soluciones del siguiente sistema:
Determina el número de soluciones de los siguientes sistemas:
- a)
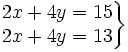
- b)
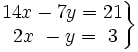
- c)
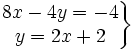
- d)
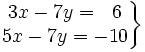
- e)
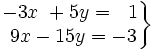
¿Cuántas soluciones tiene un sistema si tiene al menos dos?
Actividades en las que aprenderás a determinar el número de soluciones de un sistema de ecuaciones lineales con dos incógnitas y a interpretarlo gráficamente.
Actividades en las que aprenderás a determinar el número de soluciones de un sistema de ecuaciones lineales con dos incógnitas y a interpretarlo gráficamente.
En esta escena podrás interactuar para ver la representación gráfica de los distintos tipos de sistemas según el número de soluciones y contestar a algunas preguntas.
En esta escena podrás ver 3 ejemplos con los distintos tipos de sistemas según el número de soluciones y contestar a una serie preguntas en relación a ellos.
Número de soluciones de un sistema de ecuaciones: método gráfico.
Ejercicios de autoevaluación sobre los tipos de sistemas lineales dependiendo del número de soluciones.