Ecuaciones de segundo grado
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Ecuación de segundo grado
Una ecuación de segundo grado con una incógnita es aquella que se puede expresar de la forma:
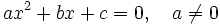
que llamaremos forma general.
Ejemplo: Ecuación de segundo grado
Pasa a forma general la ecuación:
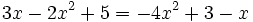
Para ponerla en forma general, pasaremos todos los términos al miembro de la izquierda:
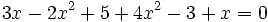
Agrupando términos semejantes:
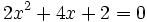
Resolución de la ecuación de segundo grado
Teorema: Fórmula de la ecuación de segundo grado
Las soluciones de la ecuación de segundo grado son:
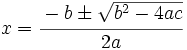
donde el signo 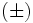 significa que una solución se obtiene con el signo
significa que una solución se obtiene con el signo 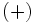 y otra con el signo
y otra con el signo 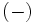 .
.
Ejemplo: Resolución de la ecuación de segundo grado
- Ejemplos de ecuaciones de segundo grado resueltas.
Pulsa "Inicio" para ver otros ejemplos:
Discriminante y número de soluciones de una ecuación de segundo grado
Llamamos discriminante de una ecuación de segundo grado a:
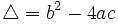
por tanto:
- Si
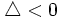 la ecuación no tiene solución.
la ecuación no tiene solución.
- Si
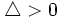 la ecuación tiene dos soluciones.
la ecuación tiene dos soluciones.
- Si
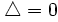 la ecuación tiene una solución (doble).
la ecuación tiene una solución (doble).
|
Actividad Interactiva: Discriminante de una ecuación de segundo grado
Actividad 1: Calcula el discriminante de las siguientes ecuaciones de segundo grado.
Actividad:
|
Ecuaciones de segundo grado incompletas
Una ecuación de segundo grado 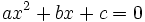 es incompleta, si ocurre uno de los siguientes casos:
es incompleta, si ocurre uno de los siguientes casos:
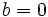 :
: 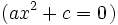
- En este caso las soluciones se obtienen despejando x:
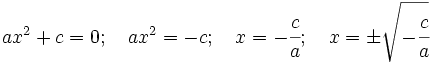
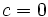 :
: 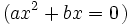
- En este caso, sacando factor común e igualando a cero cada factor:
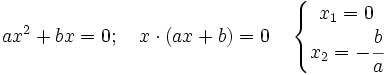
Ejemplo: Ecuaciones de segundo grado incompletas
- Ejemplos de ecuaciones de segundo grado incompletas resueltas.
Pulsa "INICIO" para ver otros ejemplos:
- Caso 1:
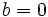 :
: 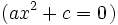
- Caso 2:
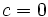 :
: