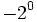Números enteros: Potencias
De Wikipedia
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Números enteros I | WIRIS Geogebra Calculadora Números enteros |
Potencias de enteros
Dependiendo del signo de la base tenemos estas dos posibilidades:
- Si la base es positiva: Al elevar un número positivo a una potencia, el resultado es positivo.
- Si la base es negativa: Al elevar un número negativo a una potencia, el resultado es positivo si el exponente es par y negativo si es impar.
Ejemplos:
|
Actividad Interactiva: Potencias de números enteros
Actividad 1. Potencias de base negativa.
Actividad: Calcula las siguientes potencias y comprueba los resultados en la escena siguiente: a) ( − 3)4 b) ( − 4)5 c) ( − 10)5 d) ( − 2)10 Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. |
Propiedades de las potencias de enteros
Las potencias de números enteros cumplen las mismas propiedades que las potencias de números naturales.
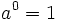
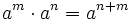
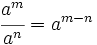
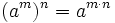
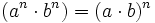
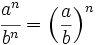
|
Ejercicios: Potencias de enteros 1. Calcula:
Solución: a) -8 b) -16 c) 64 d) 1 e) -1 f) -1 |
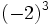 b)
b) 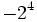 c)
c) 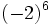 d)
d) 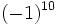 e)
e) 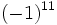 f)
f)