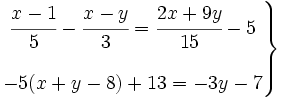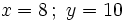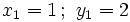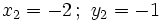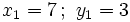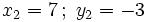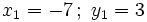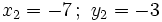Resolución de sistemas lineales y no lineales (3ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 131)
Reglas para resolver sistemas lineales
Procedimiento
Para resolver un sistema de ecuaciones lineales podemos proceder de la siguiente forma:
- Transformar las ecuaciones del sistema hasta que tengan la forma
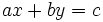 . Para ello deberás quitar denominadores y paréntesis (si los hay), transponer términos y simplificar.
. Para ello deberás quitar denominadores y paréntesis (si los hay), transponer términos y simplificar.
- Elegir un método de resolución adecuado: el método de sustitución es cómodo si alguna incógnita tiene coeficiente 1 o -1; el de reducción es cómodo si alguna incógnita tiene el mismo coeficiente en las dos ecuaciones o sus coeficientes son uno múltiplo del otro; el de igualación es cómodo por su mecánica de despejar, igualar y multiplicar en cruz.
- Podemos, opcionalmente, comprobar las soluciones. Para ello sustituiremos las incógnitas por los valores obtenidos en las dos ecuaciones del sistema de partida y los resultados deben coincidir.
Resolución de sistemas no lineales
Para resolver sistemas no lineales también podemos usar los métodos algebraicos de sustitución, igualación y reducción.
Ejercicios resueltos:
Resuelve los siguientes sistemas:
- 1.
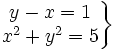
- 2.
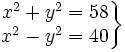
Soluciones:
1. Tiene dos soluciones:
2. Tiene cuatro soluciones:
Ejercicios propuestos
|
Ejercicios y problemas propuestos: Resolución de sistemas no lineales |
Resolución de problemas mediante sistemas
Procedimiento
Para resolver un problema mediante sistemas de ecuaciones hay que seguir los siguientes pasos:
- Determinar las incógnitas.
- Expresar el enunciado del problema en lenguaje algebraico mediante dos ecuaciones en la que intervengan las incógnitas.
- Resolver el sistema, es decir, hallar el valor de las incógnitas.
- Dar la solución del problema, a partir de los valores obtenidos de las incógnitas.
Pulsa el botón EJEMPLO para ver más problemas.
Pulsa el botón DATOS para ver otro problema similar, pero con datos diferentes.
{{Ejemplo|titulo=Ejercicios resueltos|enunciado=
- Un repostero ha mezclado 12 kg de azúcar de 1.10 €/kg con una cierta cantidad de miel de 4.20 €/kg para que la mezcla le salga a 2.34 €/kg. ¿Cuánta miel tuvo que poner?
- La distancia entre dos ciudades, A y B, es de 280 km. Untren sale de A hacia B a 80 km/h, y media hora más tarde sale un coche de B hacia A que tarda 1.2 horas en cruzarse con el tren. ¿Qué velocidad lleva el coche?
- Tres amigos trabajan 20, 30 y 50 días en un negocio. Al cabo de tres meses se reparten los beneficios y al tercero le corresponden 300 € más que al segundo. ¿Cuál es la cantidad repartida?
- Dos grifos llenan un depósito en 3 horas. Si sólo se abre uno de ellos, tardaría 5 horas. ¿Cuánto tardará el otro grifo en llenar el depósito?
|sol=
Ejercicios propuestos
|
Ejercicios y problemas propuestos: Resolución de problemas mediante sistemas |