Ángulos (3ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 184)
Ángulos
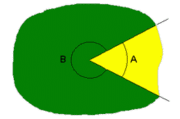
En el dibujo de la derecha puedes ver como dos semirrectas con un origen común determinan siempre dos porciones del plano y por tanto dos ángulos, A y B. Actividad en la que deberás construir un ángulo usando las herramientas de dibujo que se te proporcionan. Ángulos: definición, clasificación y medida. Ángulos: definición, clasificación y medida. Concepto de ángulo. Elementos. Amplitud. Región angular |
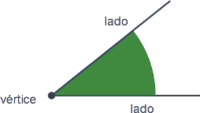
Tipos de ángulos
Clasificación de los ángulos según su amplitud
Por su amplitud, distinguimos los siguientes tipos de ángulos:
- Ángulo nulo es aquel definido por dos semirrectas que coinciden. No abarca ninguna porción del plano.
- Ángulo llano es aquel definido por dos semirrectas con la misma dirección, aunque sentidos opuestos. Abarca un semiplano, esto es, la mitad del plano.
- Ángulo convexo es aquel que es menor que un ángulo llano.
- Ángulo cóncavo es aquel que es mayor que un ángulo llano.
- Ángulo recto es aquel ángulo convexo definido por dos semirrectas perpendiculares. Abarca la cuarta parte de un plano.
- Ángulo agudo es aquel que es menor que un ángulo recto.
- Ángulo obtuso es aquel que es mayor que un ángulo recto y menor que un ángulo llano.
- Ángulo completo es aquel que abarca todo el plano.
En esta escena podrás ver una animación con los distintos tipos de ángulos según su abertura.
En este video vamos a ver cómo se clasifican los ángulos según su amplitud: rectos agudos, obtusos, llanos, completos, nulos, convexos y cóncavos.
En este video vamos a clasificar los ángulos según su amplitud de manera dinámica en: nulo, obtuso, llano, cóncavo, convexo, recto y agudo.
En este video vamos a ver la clasificación de los ángulos de acuerdo a sus medidas: ángulo agudo, ángulo recto, ángulo obtuso, ángulo llano, ángulo completo, ángulo entrante o cóncavo, ángulo negativo y ángulo nulo.
Actividad en la que comprobarás tus conocimientos sobre los tipos de ángulos.
Ángulos complementarios, suplementarios y opuestos por el vértice
Plantilla:Ángulos complementarios, suplementarios y opuestos por el vértice
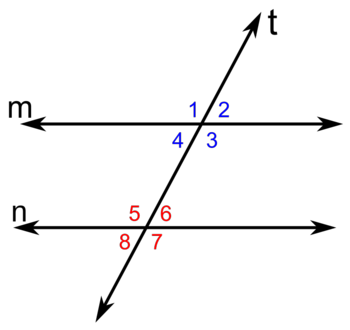
Ángulos entre dos paralelas cortadas por una transversal
Si una recta transversal corta a dos rectas paralelas:
Propiedades
En esta escena podrás ver los distintos tipos de ángulos que se forman al cortar dos rectas paralelas mediante otra recta transversal. También podrás ver cuando estos ángulos coinciden o son suplementarios. |
Ángulos en los polígonos
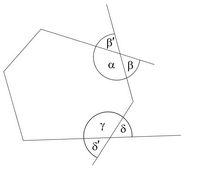
Ángulos interiores y exteriores
En el dibujo de la derecha, el ángulo |
Polígonos cóncavos y convexos
- Un polígono es convexo si todos sus ángulos interiores miden menos de 180º.
- Un polígono es cóncavo si alguno de sus ángulos interiores mide más de 180º.
Ángulos en un triángulo
Propiedad
Los tres ángulos interiores de un triángulo suman 180º.
Demostración de que la suma de los ángulos de un triángulo es un ángulo llano (180º).
En esta escena podrás ver como se obtiene la suma de los ángulos triángulo.
Ejemplos que ilustran la propiedad de que la suma de los ángulos internos de un triángulo es 180º.
Los ángulos de un triángulo miden 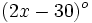 ,
, 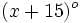 y
y 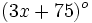 . Determina el valor de dichos ángulos.
. Determina el valor de dichos ángulos.
Ángulos en un cuadrilátero
Propiedad
Los cuatro ángulos interiores de un cuadrilátero suman 360º.
En la siguiente escena de Geogebra.
En esta escena podrás ver como se calcula la suma de los ángulos interiores de un cuadrilátero.
Halla el ángulo que falta en los siguientes cuadriláteros.
Halla los ángulos que faltan en los siguientes cuadriláteros.
Halla el ángulo que falta en el siguiente cuadrilátero.
Los ángulos de un cuadrilátero miden 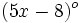 ,
, 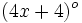 ,
, 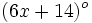 y
y 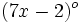 . Determina el valor de dichos ángulos.
. Determina el valor de dichos ángulos.
Ángulos en un polígono de n lados
Propiedades
- La suma de los ángulos interiores de un polígono de
 lados es igual a
lados es igual a 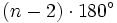 .
.
- Si el polígono de
 lados es regular:
lados es regular:
- Cada ángulo interior mide
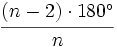 .
.
- Cada ángulo exterior mide
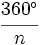 .
.
- Cada ángulo interior mide
- Desde un vértice cualquiera del polígono se pueden trazar n-3 diagonales que dividen al polígono en n-2 triángulos. Sumando los ángulos de todos esos triángulos se obtiene la fórmula, ya que la suma de los ángulos de cada triángulo es 180º.
- Si además el polígono es regular:
- Al tener todos sus ángulos interiores iguales, cada uno de ellos se obtendrá dividiendo el valor del primer apartado por el número de lados, n.
- Para ver la medida del ángulo exterior restaremos a 180º el ángulo interior:
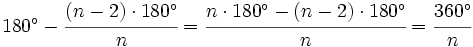
- Deducción de la fórmula de la suma de los ángulos interiores de un polígono cualquiera.
- Ejemplos de aplicación.
- Deducción de la fórmula para hallar la medida de los ángulos interiores de un polígono regular.
Deducción de la fórmula de la suma de los ángulos interiores de un polígono de n lados.
Suma de los ángulos interiores de un polígono.
- Suma de los ángulos interiores de un triángulo.
- Cálculo de los ángulos interiores de un polígono regular y de su suma.
Ángulos interiores de un cuadrado y de un hexágono regular.
¿Existe un polígono convexo cuyos ángulos sumen 1440º? Indica su nombre y la cantidad de lados que tiene.
Ángulo exterior de un polígono regular
Ángulos en la circunferencia
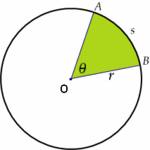
Ángulo central
En esta actividad podrás ver cómo es un ángulo central y el arco de circunferencia que determina.
Ángulo inscrito
Propiedades
Propiedades
- Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales.
- La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente.
- Todo ángulo inscrito en una semicircunferencia es recto.
Las dos primeras propiedades se pueden comprobar (no es una demostración) en la siguiente escena:
En esta escena podrás comprobar la relación que hay entre ángulos centrales y ángulos inscritos en una circunferencia.
La tercera propiedad la puedes comprobar en esta otra escena:
En esta escena podrás comprobar qué propiedad tienen todos los ángulos inscritos en una semicircunferencia.
En esta actividad podrás ver cómo es un ángulo inscrito y su relación con el ángulo central correspondiente.
En esta actividad podrás ver cómo un ángulo inscrito en una semicircunferencia es recto.
Otros ángulos
Ángulos en una circunferencia: Interior, central, inscrito, semiinscrito, interior y circunscrito.
En esta escena podrás ver los distintos tipos de ángulos que puede haber en una circunferencia: central, inscrito, semiinscrito, circunscrito, interior, exterior.
En esta escena podrás practicar el cálculo del valor de distintos tipos de ángulos en una circunferencia.
Medida de ángulos
Ejercicios propuestos
|
Ejercicios propuestos: Relaciones angulares |
 es interno y los ángulos
es interno y los ángulos 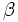 y
y  son sus correspondientes ángulos externos.
son sus correspondientes ángulos externos.
 y su arco correspondiente AB.
y su arco correspondiente AB.
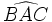 .
.