Semejanza de triángulos. Teorema de Tales (2º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 202)
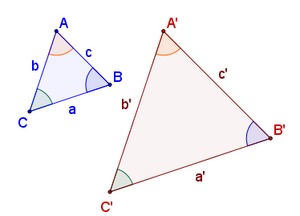
Triángulos semejantes
Se dice que dos figuras geométricas, y en particular dos triángulos, son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes.
Matemáticamente, la semejanza de triángulos la podemos expresar de la siguiente manera:
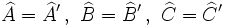
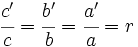
|
(*) Dos elementos de dos figuras son homólogos si ocupan el mismo lugar en ambas figuras.
Nota: Cuando veamos los criterios de semejanza de triángulos, veremos que para que dos triángulos sean semejantes bastará con que se cumpla una de las dos condiciones: que los lados homólogos sean proporcionales o que los ángulos homólogos sean iguales. En tal caso, la otra condición se cumplirá automáticamente.
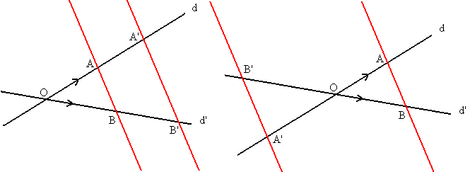
Teorema de Tales
Primer teorema de Tales
| Dos rectas paralelas, AB y A'B', que cortan a dos rectas secantes, d y d', determinan en éstas segmentos proporcionales:
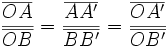 |
Demostración del primer teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
En esta escena podrás comprobar el primer teorema de Tales.
Ejercicios
Ejercicios propuestos
|
Ejercicios propuestos: Teorema de Tales |
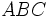
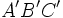
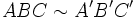
 se le llama razón de semejanza.
se le llama razón de semejanza.