Semejanza de triángulos
De Wikipedia
← Revisión anterior | Revisión siguiente →
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Triángulos | Semejanza | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Triángulos semejantes
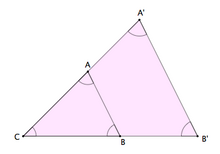
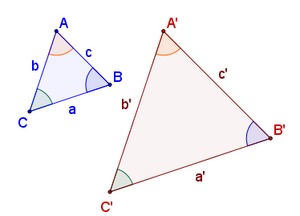
Se dice que dos figuras geométricas, y en particular dos triángulos, son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes.
Matemáticamente, la semejanza de triángulos la podemos expresar de la siguiente manera:
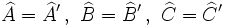
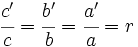
|
(*) Dos elementos de dos figuras son homólogos si ocupan el mismo lugar en ambas figuras.
Nota: Cuando veamos los criterios de semejanza de triángulos, veremos que para que dos triángulos sean semejantes bastará con que se cumpla una de las dos condiciones: que los lados homólogos sean proporcionales o que los ángulos homólogos sean iguales. En tal caso, la otra condición se cumplirá automáticamente.
Criterios de semejanza de triángulos
Los criterios de semejanza de triángulos simplifican el número de condiciones que deben comprobarse para que dos triángulos sean semejantes:
Criterios de semejanza de triángulos
- Dos triángulos son semejantes si tienen los lados proporcionales:
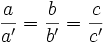
- Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales:
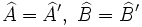
- Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo comprendido:
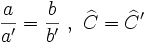
Actividades para aprender y practicar los criterios de semejanza de triángulos.
Tutorial en el que se explica y trabaja los criterios de semejanza de triángulos y se resuelven algunos ejercicios sencillos en los que se aplican dichas propiedades.
- 00:00 a 06:08: Criterios de Igualdad (Congruencia) de Triángulos.
- 06:08 a 08:30: Definición de Triángulos Semejantes.
- 08:30 a 15:30: 1er criterio de semejanza, lados proporcionales.
- 11:00 - Ejemplo del 1er criterio de semejanza.
- 15:30 a 21:30: 2º criterio de semejanza, ángulos iguales.
- 17:00 - Ejemplo del 2º criterio de semejanza.
- 21:30 a 26:30: 3er criterio de semejanza, ángulo igual y sus lados proporcionales.
- 23:05 - Ejemplo del 3er criterio de semejanza.
- 26:30 a 32:54 : Ejercicio donde se aplica la semejaza de triángulos.
Ejemplos de aplicación de los criterios de semejanza.
Los lados de un triángulo miden 3, 4 y 6 cm, y los lados de otro triángulo miden 9,12 y 18 cm. Comprueba si son semejantes.
Dos ángulos de un triángulo miden 55º y 85º, y dos de los ángulos de otro triángulo miden 55º y 65º. ¿Son semejantes?.
Cálculo altura inaccesible usando dos triángulos semejantes
En esta escena podrás ver los tres criterios de semejanza de triángulos.
Aplicaciones de los criterios de semejanza
Los criterios de semejanza que hemos visto tienen numerosas aplicaciones. Veamos algunas de ellas.
Ejercicios de aplicación de los criterios de semejanza de triángulos:
- Medición de alturas con sombras.
- Medición de alturas con espejos.
- ¿Cómo pudo medir Tales la altura de una pirámide?
En esta escena podrás hallar la altura de una casa utilizando un espejo y una cinta métrica.
Cuenta la historia que un sacerdote egipcio le preguntó a Tales de Mileto (s. IV a. C) acerca de la altura de la Pirámide de Keops, cuando ya las pirámides rondaban los 2.000 años de edad, y éste respondió con un método de lo más ingenioso para medir dicha altura..
Aplicación del teorema de la bisectriz.
Problema:
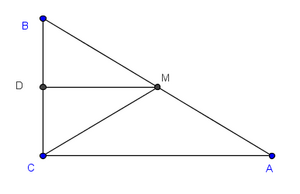
En un triángulo ABC se traza la mediana CM y desde A se traza el segmento AN que corta a la mediana CM en su punto medio T. Sabiendo que TN = 5 cm, calcula el valor de AT.
Solución:
Véase el video para ver la solución.
Demostración:
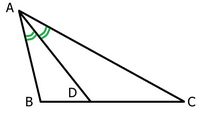
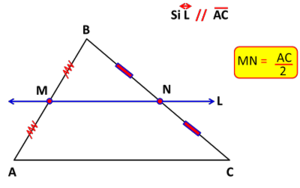
Los triángulos ABC y MBN son semejantes por estar en la posición de Tales. Además la razón de semejanza es claramente 2, por lo que lo que se nos pide es bastante inmediato.
| Problema:
Halla el valor de "x" en la figura:
Solución: Véase el video para ver la solución. | 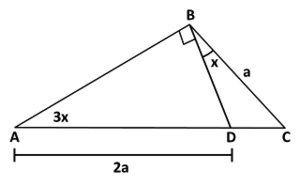
|
Teoremas del cateto y de la altura
Tutorial en el que se demuestra tanto el teorema de la altura como del cateto y aplica dichos teorema a la representación en la recta numérica de raíces cuadradas.
- 00:00 a 10:00: Demostración del Teorema de la Altura y del Cateto mediante la semejanza de triángulos.
- 10:00 a 10:35: Enunciado del Teorema de la Altura.
- 10:40 a 11:10: Enunciado del Teorema del Cateto.
- 11:10 a 15:40: Aplicación del Teorema de Pitágoras para representar raíces cuadradas..
- 15:50 a 19:45: Aplicación del Teorema de la Altura para representar raíces cuadradas..
- 19:45 a 22:15: Aplicación del Teorema del Cateto para representar raíces cuadradas.
Teoremas de la altura y del cateto. Ejemplos.
Teorema del cateto En todo triángulo rectángulo, un cateto, 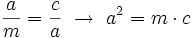 Y análogamente con el otro cateto, 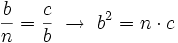 Demostración: Véase cualquiera de los siguientes videotutoriales.
Uno de los catetos de un triángulo rectángulo mide 16.5 cm y su proyección sobre la hipotenusa mide 7.5 cm. Halla el otro cateto, la proyección del otro cateto sobre la hipotenusa y la altura sobre la hipotenusa. En un triángulo rectángulo los catetos miden 20 y 21 cm. Calcula el valor de las proyecciones de los catetos sobre la hipotenusa. En un triángulo rectángulo las proyecciones de los catetos sobre la hipotenusa miden 2 y 10 cm, respectivamente. Halla a medida de los catetos. En un triángulo rectángulo uno de los catetos mide 12 cm, y su proyección sobre la hipotenusa 9 cm. Calcula la hipotenusa y el otro cateto. En un triángulo rectángulo las proyecciones de los catetos sobre la hipotenusa miden 25 y 36 m, respectivamente. Halla a medida de la hipotenusa. Teorema de la altura En todo triángulo rectángulo, la altura, 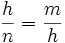 Demostración: Véase cualquiera de los siguientes videotutoriales:
Las proyecciones de los actetos sobre la hipotenusa de un triángulo rectángulo miden 18 m y 32 m, respectivamente. Halla la medida de los catetos y la de la altura sobre la hipotenusa. Problema de aplicación del teorema de la altura En un triángulo rectángulo las proyecciones de los catetos sobre la hipotenusa miden 2 y 10 cm, respectivamente. Halla la altura sobre la hipotenusa. Una torre eléctrica está sujeta al suelo con dos tensores. La distancia entre los pies de ambos tensores es 50 m. Los cables que sujetan la torre forman un ángulo recto y miden 30 y 40 m, respectivamente. Calcula la altura de la torre. En un triángulo rectángulo los catetos miden 20 y 21 cm, respectivamente. Calcula la altura del triángulo que cae sobre la hipotenusa. |
Relación entre las áreas de figuras semejantes
En este video exploraremos el comportamiento del área respecto a la longitud de los lados de un triángulo equilátero.
Teorema de Tales
Primer teorema de Tales
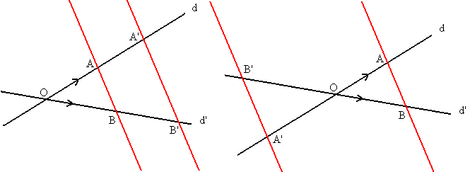
| Dos rectas paralelas, AB y A'B', que cortan a dos rectas secantes, d y d', determinan en éstas segmentos proporcionales:
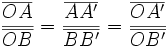 |
Demostración del primer teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
Ejemplo de aplicación del teorema de Tales.
En esta escena podrás comprobar el primer teorema de Tales.
Triángulos en la posición de Tales
Dos triángulos ABC y A'B'C', con sus lados paralelos y encajados con un vértice común, se dice que están en la posición de Tales Teorema de Tales. Ejemplos. Tutorial en el que se explica y trabaja el teorema de Tales y se resuelven algunos ejercicios sencillos en los que se aplican dichas propiedades.
División de un segmento en partes proporcionales. Dibujo y cálculo del 4º proporcional a tres segmentos dados. Cálculo y dibujo del 3º proporcional a dos segmentos dados. Ejercicio de aplicación del primer teorema de Tales. Ejercicio de aplicación del primer teorema de Thales. Otra forma equivalente de enunciar el teorema de Tales utilizando la semejanza de triángulos: Dos triángulos encajados (en la posición de Tales) son semejantes y en consecuencia sus lados son proporcionales. Ejemplo de aplicación del teorema de Tales. Ejemplo de aplicación del teorema de Tales. Ejemplo de aplicación del teorema de Tales. Ejemplo de aplicación del teorema de Tales. Ejemplo de aplicación del teorema de Tales. Ejemplo de aplicación del teorema de Tales. |
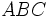
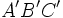
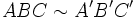
 se le llama razón de semejanza.
se le llama razón de semejanza.
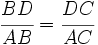
 , es media proporcional entre la hipotenusa,
, es media proporcional entre la hipotenusa, 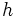 , y la proyección,
, y la proyección,  , de dicho cateto sobre la hipotenusa,
, de dicho cateto sobre la hipotenusa,  .
.
 , y su proyección,
, y su proyección,  .
.