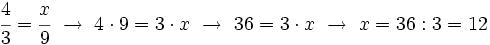Fracciones equivalentes (1º ESO)
De Wikipedia
← Revisión anterior | Revisión siguiente →
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 125)
Fracciones equivalentes
| El siguiente videotutorial condensa todo lo que se va a ver en este tema sobre fracciones equivalentes:
Tutorial que explica el concepto de fracciones equivalentes y como obtener la fracción irreducible a una dada.
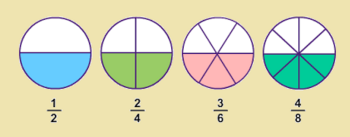
Dos fracciones son equivalentes si tienen el mismo valor. En la Fig.1 tienes ejemplos de fracciones equivalentes. Fíjate como representan la misma porción de la unidad aunque sus numeradores y denominadores sean diferentes.
Introducción a fracciones equivalentes. Modelos de fracciones equivalentes. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe las fracciones que representen cada uno de los puntos representados en la recta numérica. ¿Qué puedes decir de esas fracciones? Escribe las fracciones que representen cada uno de los puntos representados en la recta numérica. ¿Qué puedes decir de esas fracciones? Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Calcula cuatro fracciones equivalentes a Calcula cuatro fracciones que representen al número racional |
Obtención de fracciones equivalentes
| Piensa un número. Multiplícalo por 2. Divide el resultado entre 2. ¿Qué sucede?. Lógicamente, el número vuelve a ser el que era al principio porque la multiplicación y la división son operaciones inversas.
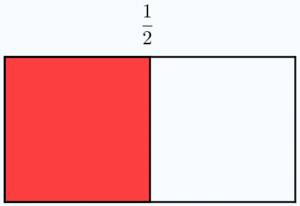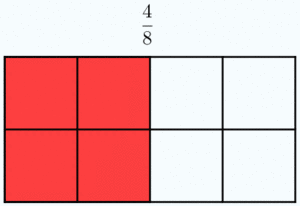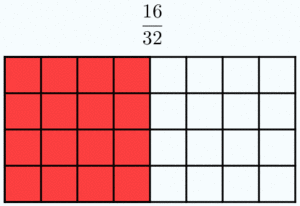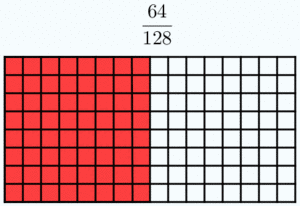
Esta idea, junto al hecho de que las fracciones sean el cociente de dos números enteros, permite que muchas fracciones representen el mismo número racional. Más que muchas, infinitas. Piensa, por ejemplo, en la fracción 1/2. Si multiplicamos su numerador y su denominador por el mismo número entero distinto de cero, en realidad, no estamos variando el valor de la fracción. Gráficamente, multiplicar el numerador y el denominador de una fracción por el mismo número significa partir el "todo" que estamos considerando en piezas más pequeñas, pero en realidad no varía la cantidad de ese "todo" que se toma. Fíjate en la animación para entenderlo mejor. |
Obtención de fracciones equivalentes
Si se multiplica o se divide (de forma exacta) el numerador y el denominador de una fracción por un mismo número distinto de cero, se obtiene una fracción equivalente. Si además el número por el que multiplicamos o dividimos es distinto de 1, estos procedimientos reciben el nombre de amplificación y simplificación, respectivamente.
En realidad, estos dos procesos son inversos el uno del otro. La única diferencia importante entre uno y otro es que, mientras la amplificación se puede hacer siempre, la simplificación sólo es posible si el numerador y el denominador tienen un divisor común mayor que 1.
Amplificación
| Simplificación
|
Obtención de fracciones equivalentes: por amplificación y por simplificación.
Obteniendo fracciones equivalentes por simplificación.
Obteniendo fracciones equivalentes por amplificación y simplificación.
Obtén dos fracciones equivalentes a 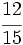 : una por amplificación y otra por simplificación.
: una por amplificación y otra por simplificación.
Escribe tres fracciones equivalentes a 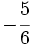 por amplificación.
por amplificación.
Escribe tres fracciones equivalentes a 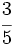 por amplificación.
por amplificación.
Escribe tres fracciones equivalentes a 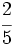 por amplificación.
por amplificación.
Escribe dos fracciones equivalentes a 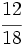 por amplificación.
por amplificación.
Halla una fracción equivalente a 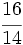 por amplificación y otra por simplificación.
por amplificación y otra por simplificación.
Escribe dos fracciones equivalentes a 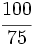 por simplificación.
por simplificación.
Escribe dos fracciones equivalentes a 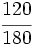 por simplificación.
por simplificación.
Escribe tres fracciones equivalentes a 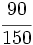 por simplificación.
por simplificación.
Busca una fracción equivalente a la dada con la ayuda del gráfico.
- a) Escribe una fracción equivalente a la dada.
- b) Empareja las fracciones equivalentes.
Fracciones equivalentes. Representación en la recta numérica.
Encontrar fracciones equivalentes por medio de la multiplicación.
Completa la fracción para que se cumpla la igualdad.
Completa la fracción para que se cumpla la igualdad.
Completa la fracción para que se cumpla la igualdad.
Encontrar fracciones equivalentes por medio de la multiplicación.
Simplificación de fracciones
- Simplificar una fracción es sustituirla por otra equivalente con el numerador y denominador menores que los de partida.
- Cuando una fracción no se puede simplificar se dice que es irreducible.
Procedimiento: Simplificación
- Para simplificar fracciones se divide numerador y denominador por un mismo número, distinto de 0 y 1. Este proceso se puede repetir hasta hacer la fracción irreducible.
- Si queremos hacer la fracción irreducible en un solo paso debemos dividir numerador y denominador por el m.c.d. de ambos.
Simplifica 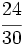 :
:
Solución:
- Paso a paso: Dividimos por 2 y luego por 3
- En un solo paso: Calculamos el m.c.d.(24,30) = 6, y dividimos directamente por 6:
Simplificación de fracciones (3 métodos). Fracción irreducible. Ejemplos.
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: | Simplifica: Simplifica: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: |
- Actividades en las que deberás simplificar fracciones con o sin ayuda.
- Actividad en la que debes emparejar cada fracción con su irreducible.
Actividad en las que deberás encontrar la fracción irreducible.
Actividades de nivel variable en las que deberás simplificar fracciones.
Simplifica fracciones.
La simplificación de fracciones me proporciona un método para saber si dos fracciones son equivalentes.
Procedimiento
Si al simplificar dos fracciones se obtiene la misma fracción irreducible, entonces las dos fracciones son equivalentes.
Determina si 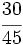 y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
son fracciones equivalentes.
Ejercicios propuestos
|
Ejercicios propuestos: Fracciones equivalentes |
Relación entre los términos de dos fracciones equivalentes
Cómo averiguar si dos fracciones son equivalentes
Con lo que llevamos visto hasta ahora, tenemos dos formas de comprobar que dos fracciones son equivalentes:
- Calculando el valor de cada una de ellas, dividiendo numerador entre denominador, y viendo si el resultado es el mismo.
- Calculando la fracción irreducible de cada una de ellas y viendo si ambas fracciones irreducibles son iguales.
A continuación vamos a ver un resultado que permite hacer la comprobación de forma más simple. Lo llamaremos el método de multiplicar "en cruz".
Comprobación de que dos fracciones son equivalentes
Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden.
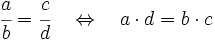
Cómo averiguar el término que falta en una igualdad entre fracciones
Si nos dan dos fracciones equivalentes y en una de ellas desconocemos uno de sus términos, utilizaremos el resultado anterior para averiguarlo.
Cálculo del término desconocido en una proporción. Ejemplos.
- Actividad 2a: Deberás escribir una fracción equivalente a la dada y verás la comprobación por el método de los productos cruzados.
- Actividad 2b: Actividad guiada en la que debes encontrar el término que falta de una igualdad entre fracciones.
Actividad en la que debrás averiguar el término que falta en una igualdad de fracciones.
Ejercicios propuestos
|
Ejercicios propuestos: Relación entre los términos de dos fracciones equivalentes |
Actividades
- Escribe, para cada apartado, las tres fracciones equivalentes que resultan de multiplicar el numerado y el denominador de la fracción dada por 2, 3 y 4, en ese orden.
- Encuentra la fracción irreducible para cada apartado.
- De la siguientes parejas de fracciones, señala aquellas que sean equivalentes.
- Completa para que las igualdades sean ciertas.
Ejercicios sobre fracciones equivalentes.
Ejercicios de autoevaluación sobre fracciones propias e impropias, fracciones equivalentes, fracciones irreducibles.
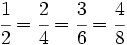
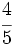 y
y 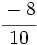 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
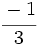 y
y 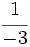 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
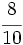 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
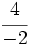 y
y 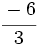 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
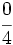 y
y 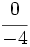 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
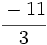 y
y 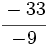 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
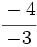 y
y 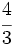 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
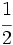 y represéntalas en la recta numérica. ¿Qué observas?
y represéntalas en la recta numérica. ¿Qué observas?
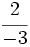 y represéntalas en la recta numérica.
y represéntalas en la recta numérica.
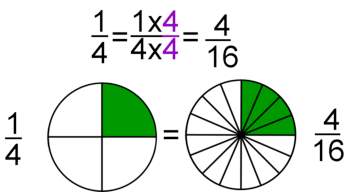
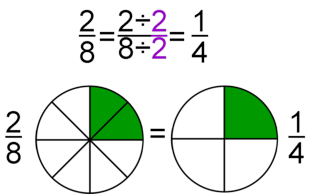
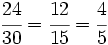
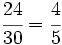
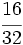 b)
b) 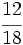
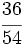 b)
b) 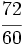
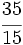 b)
b) 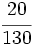
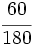 b)
b) 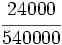
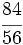 b)
b) 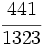
 b)
b) 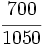
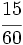
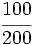 .
.
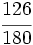 .
.
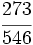 .
.
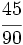 .
.
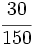 .
.
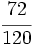 .
.
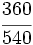 .
.
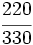 .
.
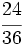 .
.
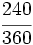 .
.
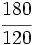 .
.
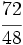 .
.
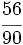 .
.
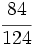 .
.
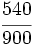 .
.
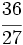 .
.
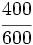 .
.
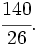
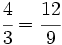 , porque
, porque 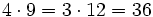 (son equivalentes)
(son equivalentes)
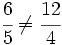 , porque
, porque 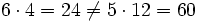 (no son equivalentes)
(no son equivalentes)
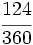 y
y 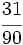 ?
?