El conjunto de los números naturales (2º ESO)
De Wikipedia
← Revisión anterior | Revisión siguiente →
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Sistemas de numeración (1º ESO) | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 10)
El conjunto de los números naturales
El conjunto de los números naturales es:
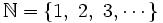
Se trata de un conjunto con infinitos elementos y sirven para:
- Contar (números cardinales: 1, 2, 3, ...).
- Ordenar (números ordinales: 1º, 2º, 3º, ...).
- Identificar y diferenciar los distintos elementos de un conjunto.
Puesto que los números naturales se utilizan para contar elementos, el cero (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero.
Veamos distintos ejemplos de uso de los números naturales:
- Como número cardinal: Los días de la semana son 7.
- Como número ordinal: El atleta británico quedó 3º en la prueba de cien metros lisos.
- Como identificador: Tú número de carnet de socio del Atleti es el 2868.
El conjunto de los números naturales: origen y definición.
El conjunto de los números naturales: origen y definición.
Tutorial de introducción al tema:
- Números naturales.
- Sistemas de numeración.
- Sistema de numeración decimal.
Hace unas horas tenía 16 años y el año que viene cumpliré 19. ¿Cómo explicas esta situación?
Ejercicios de autoevaluación sobre números naturales.
Existen dos teorías sobre el origen de la numeración, que además está relacionada con la cuestión de qué números aparecieron primero, los cardinales (1, 2, 3,...) o los ordinales (1º, 2º, 3º,...) La teoría que genera más consenso defiende el argumento de la necesidad. Todo habría comenzado a causa de la necesidad de contar objetos; por ello se habrían creado primero los números cardinales y después, los ordinales.
La otra teoría defiende la base espiritual de los números, que habrían tenido un uso ritual: cierto tipo de ceremonias requerían que los participantes se desplazaran o se situaran en un orden ritual preestablecido; por eso los números ordinales serían anteriores a los cardinales. Esta teoría además postula que los números se originaron en un lugar geográfico determinado, desde el que se propagaron al resto del mundo; también establece la división de los números naturales en pares e impares, considerando los impares masculinos y los pares, femeninos, una clasificación que comparten hoy en día muchas culturas del planeta.
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 10)"
Véanse los artículos de la BBC:
- ¿Sabes que el 1 y el 2 no son del mismo género y que los números tienen personalidades?
- Lo que quizás no sabías de los números
Sistemas de numeración
| Los números surgen de la necesidad de contar. Por ejemplo, el hombre primitivo, para contar los animales de su rebaño, hacia uso de semillas o guijarros; muescas en palos, huesos o piedras; etc.
En numerosas civilizaciones el hombre uso su cuerpo, dándole a sus partes (manos, pies, falanges, ...) valores numéricos. A medida que la sociedad fue evolucionando, surgió la necesidad de contar cantidades más grandes, para lo que hubo que inventar nuevos símbolos. Los símbolos utilizados para representar los números y sus normas de uso forman un sistema de numeración. |

(Wikipedia)
Las pruebas más remotas del empleo de los números son los huesos con marcas hallados en excavaciones arqueológicas. El más antiguo descubierto hasta la fecha posee 35 000 años de antigüedad; se trata de un hueso de papio (primate popularmente conocido como babuino) encontrado en la coordillera de Lebombo, en Suazilandia (África), en el curso de una excavación realizada en 1973. Contiene 29 marcas y se cree que debía de utilizarse como contador de las fases lunares, aunque quizá se usara también para seguir el ciclo menstrual. Su aspecto es parecido al de los bastones que aún hoy en día utilizan los bosquimanos de Namibia.
Otro hallazgo destacado es un hueso de lobo descubierto en 1937 en Vestonice, en la región checa de Moravia, que posee 55 marcas agrupadas de 5 en 5 y una marca adicional después de la marca 25; pertenece a la cultura auriñaciense y tiene unos 30 000 años de antigüedad. En sus proximidades se halló también la cabeza de una Venus de marfil.
El siguiente ejemplar destacado es mas "reciente"; se trata del llamado "hueso de ishango", que fue hallado en el Congo en 1960 y tiene unos 20 000 años de antigüedad.
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 9)"
El hueso de Ishango es un utensilio de hueso que data del Paleolítico superior, aproximadamente del año 20 000 a. C. Este objeto consiste en un largo hueso marrón (más específicamente, el peroné de un papio con un pedazo punzante de cuarzo incrustado en uno de sus extremos, quizás utilizado para grabar o escribir. En un principio se pensaba que se empleaba como palo de conteo, ya que el hueso tiene una serie de muescas talladas divididas en tres columnas que abarcan toda la longitud de la herramienta, pero algunos científicos han sugerido que las agrupaciones de muescas indican un conocimiento matemático que va más allá del conteo. No obstante para algunos autores que no descartan la perspectiva del conteo primigenio, el hueso de Ishango representa el origen de la contabilidad, o al menos de la racionalidad del conteo que permitió la civilización.
Alexander Marshack examinó el hueso de Ishango con un microscopio y concluyó que esta antigua herramienta puede representar un calendario lunar de seis meses. Claudia Zaslavsky ha sugerido que esto puede indicar que el creador del instrumento era una mujer, investigando la relación entre las fases lunares con el ciclo menstrual.
El belga Jean de Heinzelin de Braucourt encontró en 1960 el hueso de Ishango mientras exploraba lo que entonces era el Congo Belga. Lo descubrió en el área africana de Ishango, cerca de la zona donde nace el río Nilo, en el lago Eduardo (que se encuentra entre la frontera de Uganda y la República Democrática del Congo). Esto significa que la población establecida hace unos 20 000 años a orillas del lago en Ishango pudo haber sido una de las primeras sociedades en realizar conteos, pero esta sociedad tan solo sobrevivió unos pocos cientos de años antes de quedar sepultada por una erupción volcánica.
En un principio se estimó que el hueso databa de entre los años 9000 a. C. y 6500 a. C. Sin embargo, la datación del sitio donde fue descubierto fue revaluada y ahora se cree que tiene más de 20 000 años.
El hueso de Ishango se exhibe de forma permanente en el Real Instituto Belga de Ciencias Naturales de Bruselas, Bélgica.
(Extracto de Wikipedia)
Tipos de sistemas de numeración
A lo largo de la historia ha habido diferentes sistemas de numeración. Podemos distinguir dos tipos de sistemas de numeración: aditivos y posicionales.
Algunos sistemas de numeración son mixtos, es decir, tienen algo de aditivos y algo de posicionales. (Ej. sist. num. romano, maya y babilónico). Tutorial que muestra una breve introducción a los sistemas de numeración: aditivos, multiplicativos y posicionales. Explicación de algunos de los más importantes sistemas de numeración a lo largo de la historia, del egipcio hasta el binario, pasando por el babilónico, griego, maya, chino, hindú... - 00:00 a 01:30: Introducción. - 01:30 a 03:41: Sistema Egipcio. Sistema Aditivo. - 03:41 a 07:40: Sistema Babilónico. Sistema Posicional. - 07:40 a 10:10: Sistema Griego. Sistema Aditivo. - 10:10 a 12:10: Sistema Chino. Sistema Multiplicativo. - 12:10 a 16:00: Sistema Maya. Sistema Posicional. - 16:00 a 17:10: Sistema Romano. Sistema Aditivo. - 17:10 a 22:20: Sistema Hindú. Sistema Posicional. + 18:45 : Sistema Decimal. - 22:20 a 25:42: Sistemas de Numeración en la Informática (Binario, Octal, Hexadecimal). Si quieres ser más geek, tienes que aprender el código binario, un sistema numérico de base dos. ¿Te animas a conocer este método de codificación con ceros y unos? Tutorial que explica a fondo el sistema de numeración binario, tanto su fundamento como su paso al sistema decimal y viceversa. El video comienza recordando qué es un sistema de numeración y la mecánica del sistema de numeración decimal. También se dan algunas pinceladas del sistema hexadecimal y octal. Una mirada con humor a los primeros intentos de crear sistemas de numeración, que conducen a nuestro moderno sistema decimal de base 10, el cual hace uso de la "notación posicional". La historia transcurre en la ficticia isla de Cocoloco. Our modern decimal number system is base-10. Other number systems used in fields like computer engineering are base-2 (binary), base-8 (octal) and base-16 (hexadecimal). (Disponibles los subtítulos en inglés) Con la llegada del euro volverán los céntimos y unos viejos conocidos van a adquirir un protagonismo social que no tenían desde hace mucho tiempo: los números decimales. Unos números que, a pesar de la creencia popular de que existen desde los comienzos de las matemáticas, sólo llevan entre nosotros cuatro siglos. Y es que la historia de los números es más compleja de lo que sospechamos. A lo largo del programa haremos una excursión por el tiempo para descubrir la historia de las cifras. Descubriremos las cifras y la forma de utilizarlas de babilonios, egipcios, griegos y romanos hasta llegar hasta nuestras populares 10 cifras: 1, 2, 3, 4, 5… Pero incluso estas cifras heredadas de los árabes no siempre han sido la herramienta habitula para calcular. Conoceremos las aventuras de estos símbolos desde su nacimiento hasta nuestros días, en que sin duda son los símbolos más universalmente utilizados. ¿Para qué sirven los números romanos? ¿Cuáles son los números romanos? ¿Y sus reglas? ¿Cuál es su origen? Descubre los números romanos y aprende a escribir como lo hicieron nuestros antepasados. Sistema de numeración romano. Reglas. Cómo pasar del sistema de numeración romano al decimal y del sistema decimal al romano. Ejemplos. Números romanos son un sistema antiguo de numeración decimal. La comprensión de las cifras romanas (con notación aditiva) puede arrojar luz sobre nuestro moderno sistema de numeración que emplea notación posicional. Tutorial que explica a el sistema de numeración maya. Tutorial que explica a el sistema de numeración maya. Tutorial que explica a el sistema de numeración maya y las operaciones de suma, resta, multiplicación y división.
|
Ejercicios propuestos
|
Ejercicios propuestos: El conjunto de los números naturales |