Ley de Laplace (3ºESO)
De Wikipedia
| Revisión de 08:08 3 jun 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:09 3 jun 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 18: | Línea 18: | ||
| }} | }} | ||
| <br> | <br> | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/wiki_Estadistica/Azar_y_Probabilidad/probable.html | ||
| + | width=100% | ||
| + | height=150 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| <br> | <br> | ||
| + | |||
| {{Ejemplo|titulo=Ejemplo: ''Ley de Laplace'' | {{Ejemplo|titulo=Ejemplo: ''Ley de Laplace'' | ||
| |enunciado= | |enunciado= | ||
| Línea 27: | Línea 34: | ||
| P(OROS)=número de oros/número total de cartas=10/40=0.25 | P(OROS)=número de oros/número total de cartas=10/40=0.25 | ||
| }} | }} | ||
| - | <br> | + | {{p}} |
| - | <br> | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/wiki_Estadistica/Azar_y_Probabilidad/probable.html | + | |
| - | width=100% | + | |
| - | height=150 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <br> | + | |
| {{Video | {{Video | ||
| |titulo=Las Leyes del Azar | |titulo=Las Leyes del Azar | ||
Revisión de 08:09 3 jun 2009
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Ley de Laplace
Definición de probabilidad de Laplace. En el caso de que todos los sucesos elementales del espacio muestral E sean equiprobables, Laplace define la probabilidad del suceso A como el cociente entre el número de resultados favorables a que ocurra el suceso A en el experimento y el número de resultados posibles del experimento.
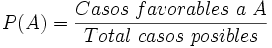
|
Ejemplo: Ley de Laplace
En una baraja de 40 cartas, ¿cuál es la probabilidad de AS?, ¿Y de OROS
P(As)=número de ases/número total de cartas=4/40=0.1
P(OROS)=número de oros/número total de cartas=10/40=0.25Video: Las Leyes del Azar (17´)
El ser humano siempre ha estado preocupado por lo que le deparará el futuro. Las matemáticas han intentado iluminar, al menos en parte, las pautas que rigen el futuro inmediato sujeto al azar. En nuestro país nos gastamos todas las semanas miles de millones de pesetas en loterías, bonolotos, primitiva, sorteos... Ponemos nuestra suerte y nuestro dinero en manos del azar. Pero el azar tiene sus leyes y en algunas de esas leyes profundizaremos en este programa. Descubriremos, entre otras, cosas la probabilidad de acertar un pleno en la primitiva. Lo que empezó como un juego, un problema de dados planteado a Pascal, se ha convertido en la Teoría de la Probabilidad, una de las herramientas matemáticas más utilizadas en la actualidad. Desde loa aficionados a los juegos de azar, hasta las aseguradoras y las multinacionales toman sus decisiones basándose en las Leyes del Azar.
|
Ejercicios: Cálculo de probabilidades 1. Si escogemos al azar dos números de teléfono y observamos la última cifra de cada uno, determina las probabilidades siguientes: a) Que las dos cifras sean iguales b) Que su suma sea 11 c) Que su suma sea mayor que 7 y menor que 13Solución: a) El espacio muestral de este experimento está formado por los cien sucesos elementales: 00, 01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 11, ..., 98, 99. Para cada sucesos del enunciado calculamos sus casos favorables, aplicamos la regla de Laplace y obtenemos: Los casos favorables son: 00, 11, 22, ..., 99. La probabilidad de que las últimas cifras sean iguales es: P(últimas cifras iguales) = 10/100 = 1/10 = 0.1 Los casos favorables a que la suma de las últimas cifras sea 11 son: 29, 38, 47, 56, 65, 74, 83 y 92. Por tanto, b) P(últimas cifras suman once) = 8/100 = 0.08 c) Deben contarse los números de dos cifras cuya suma sea 8, 9, 10, 11 y 12. Haciendo un recuento ordenado, se obtienen 43 casos favorables. La probabilidad buscada es: P(últimas cifras suman un valor mayor que 7 y menor que 13) = 43/100 = 0.432. Se lanzan dos dados equilibrados con seis caras marcadas con los números del 1 al 6. Se pide: a) Halla la probabilidad de que la suma de los valores que aparecen en la cara superior sea múltiplo de tres. b) ¿Cuál es la probabilidad de que los valores obtenidos difieran en una cantidad mayor de dos?Solución: a) El espacio muestral del experimento es: E = {(1,1); (1,2); (1,3); (1,4); (1,5); (1,6); (2,1); ...; (6,6)} y está formado por 36 sucesos elementales equiprobables. Constituyen el número de casos posibles del experimento. Utilizando la regla de Laplace, calculamos las probabilidades de los sucesos que nos piden: Si llamamos A al suceso "obtener una suma múltiplo de 3", los casos favorables al suceso A son: A = {(1,2); (2,1); (1,5); (2,4); (3,3); (4,2); (5,1); (3,6); (4,5); (5,4); (6,3); (6,6)}. Por tanto, P( A ) = 12/36 = 1/3
B = {(1,4); (4,1); (1,5); (5,1); (1,6); (6,1); (2,5); (5,2); (2,6); (6,2); (3,6);(6,3)}.
3.Se tiran tres dados al mismo tiempo. Encuentra la probabilidad de que: a) La suma de los números aparecidos sea menor que 8. b) La suma de los números sea mayor que 4 y menor que 8.Solución: Los casos posibles de este experimento son las 216 ternas siguientes: 111, 112, 121, 211, ..., 665, 666. Realizando un recuento ordenado de los casos favorables a los sucesos del enunciado, obtenemos las siguientes probabilidades: a) P(suma de valores menor que 8)= 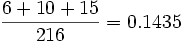 |