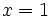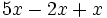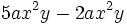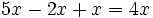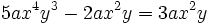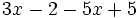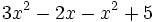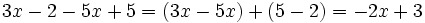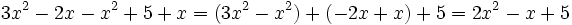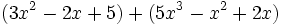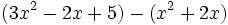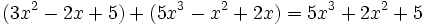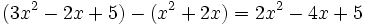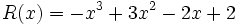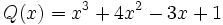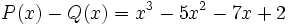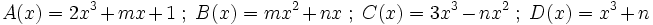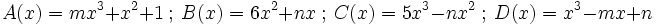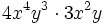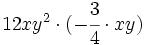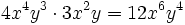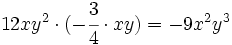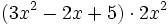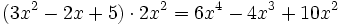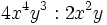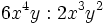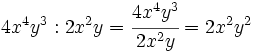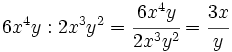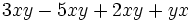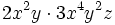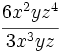Expresiones algebraicas (1º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 172)
Expresiones algebraicas
- Una expresión algebraica es una combinación de letras y números ligados por las operaciones matemáticas (suma, resta, multiplicación, división, potenciación, radicación, ...), que respeta las reglas del lenguaje algebraico.
- Las letras, que suelen representar cantidades desconocidas, no tienen un valor fijo y se denominan variables. Los números se denominan constantes porque tienen un valor fijo.
- Se puede usar cualquier letra del alfabeto para expresar una variable, excepto la "e" y la "i", porque están reservadas para unos números especiales. Las letras más habituales son x, y, z, a, b, c, ...
- Las reglas que se mencionan en la definición son las mismas que ya teníamos en cuenta al trabajar únicamente con números y alguna otra que aparecerá más adelante. Entre ellas tenemos:
- Dos símbolos de operación no pueden aparecer juntos sin estar separados por otro elemento (paréntesis, corchetes, raya de fracción...)
- Cuando realizamos una operación combinada en varias etapas, cada una de ellas tiene que estar precedida del símbolo =, y los elementos que no se operan deben repetirse en la misma posición o en una equivalente, siempre respetando las propiedades de las operaciones.
- Si el símbolo = está seguido por una raya de fracción, ésta debe aparecer a una altura intermedia entre las dos rayas del igual.
- El número 1 puede omitirse cuando está multiplicando a otro número o cuando actúa como exponente.
- El símbolo de la multiplicación puede omitirse cuando a continuación del mismo aparecen unos paréntesis, o cuando se indica el producto de dos variables (letras).
- ...
Expresiones algebraicas: definición y ejemplos.
Expresiones algebraicas. Tipos de expresiones algebraicas: enteras y fraccionarias.
Indica si las siguientes expresiones algebraicas son enteras o fraccionarias:
- 44)
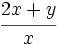 ; 45)
; 45) 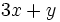 ; 46)
; 46) 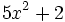
- 47)
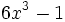 ; 48)
; 48) 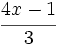 ; 49)
; 49) 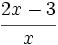
- 50)
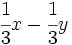
Ejemplos de expresiones algebraicas.
Actividad en la que deberás encontrar la expresión algebraica adecuada para cada situación.
Actividad en la que deberás encontrar la expresión algebraica adecuada para cada situación.
Tipos de expresiones algebraicas
Hay distintos tipos de expresiones algebraicas. Nosotros nos vamos a centrar, de manera especial, en unas que llamaremos monomios y polinomios.
- Monomio: es una expresión algebraica que consta de un número (coeficiente), multiplicado por letras (variables) con exponentes naturales.
- Polinomio: es la suma de varios monomios. Algunos polinomios tienen nombre propio: binomio (2 sumandos), trinomio (3 sumandos), ...
En general, cuando hablemos de polinomios, nos referiremos tanto a los monomios como a los polinomios. Es decir, un monomio lo veremos como un polinomio con un solo sumando.
- Monomios:
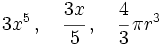
- Polinomios:
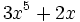 (binomio)
(binomio)
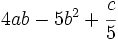 (trinomio)
(trinomio)
- No son monomios, ni polinomios:
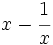 , porque la variable aparece dividiendo.
, porque la variable aparece dividiendo.
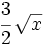 , porque la variable aparece dentro de una raíz.
, porque la variable aparece dentro de una raíz.
Elementos que componen una término algebraico.
Elementos que componen una expresión algebraica. Clasificación de las expresiones algebraicas.
Monomios, binomios, trinomios y polinomios. Ejemplos.
Actividad en la que deberás decir de qué tipo es la expresión algebraica dada.
Valor numérico de una expresión algebraica
| El lenguaje algebraico sirve para pasar de casos particulares a casos generales, sin embargo, en muchas ocasiones haremos el proceso inverso, pasaremos de una expresión general a un valor concreto.
Si en una expresión algebraica se sustituyen las letras (variables) por números y se realizan las operaciones correspondientes, se obtiene un número al que llamaremos el valor númerico de la expresión algebraica para los valores de las letras asignados. |
Ejemplo: Valor numérico de una expresión algebraica
Halla el valor numérico:
- a)
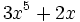 para
para 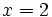
- b)
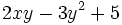 para
para 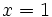 e
e 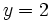 .
.
a) El valor numérico es: 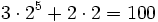
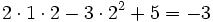
Tutorial en el que se explica y trabaja el cálculo del valor numérico de expresiones algebraicas de una o más variables, así como las tablas de valores.
En este video vamos a ver lo que es el valor numérico de una expresión algebraica y cómo se calcula.
Calcula el valor numérico de la expresión algebraica 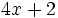 para
para 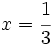 .
.
Calcula el valor numérico de la expresión algebraica 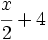 para
para 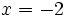 .
.
Calcula el valor numérico de la expresión algebraica 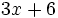 para
para 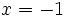 .
.
Calcula el valor numérico de la expresión algebraica 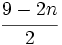 para
para 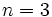 .
.
Calcula el valor numérico de la expresión algebraica 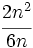 para
para 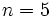 .
.
Calcula el valor numérico de la expresión algebraica 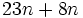 para
para 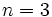 .
.
Calcula el valor numérico de la expresión algebraica 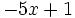 para
para 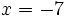 .
.
Calcula el valor numérico de las siguientes expresiones algebraicas para los valores indicados de las variables:
- 51)
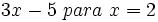
- 52)
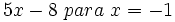
- 53)
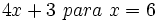
- 54)
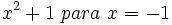
- 55)
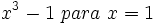
- 56)
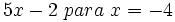
- 57)
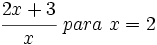
- 58)
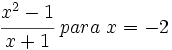
- 59)
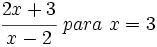
Un hospital local está realizando una rifa para recolectar fondos. El coste individual para participar en la rifa está dado por la expresión 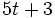 , donde
, donde 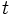 representa el número de boletos que la persona adquiere. Evalúa la expresión para
representa el número de boletos que la persona adquiere. Evalúa la expresión para 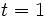 ,
, 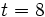 y
y 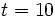 .
.
- a) Evalúa la expresión
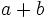 para
para 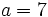 y
y 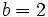 .
.
- b) Evalúa la expresión
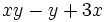 para
para  e
e 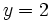 .
.
- a) Evalúa la expresión
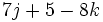 para
para 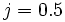 y
y 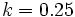 .
.
- b) Evalúa la expresión
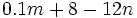 para
para 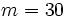 y
y  .
.
- a) ¿Qué le ocurre a la expresión
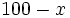 cuando la variable
cuando la variable  va disminuyendo?
va disminuyendo?
- b) ¿Qué le ocurre a la expresión
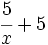 cuando la variable
cuando la variable  va disminuyendo, pero manteniéndose positiva?
va disminuyendo, pero manteniéndose positiva?
Expresa 25º Celsius (C) como una temperatura en grados Fahrenheit (F), usando la fórmula:
El área de la superficie de un cubo es igual a la suma de las áreas de sus 6 caras. En consecuencia, vendrá dada por la fórmula 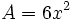 , siendo
, siendo  el valor de la arista del cubo.
el valor de la arista del cubo.
Julia tiene dos recipientes de forma cúbica que quiere pintar. Uno tiene arista 2 y otro 1.5. Calcula el área total que quiere pintar.
Evalúa la expresión 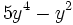 cuando
cuando 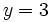 .
.
Actividades en la que aprenderás y practicarás el cálculo del valor numérico de una expresión algebraica.
Actividades en la que aprenderás y practicarás el cálculo del valor numérico de una expresión algebraica.
Evaluar expresiones con una sola variable.
Evaluar expresiones con dos variables.
Evaluar expresiones con dos variables: fracciones y decimales.
Intuición sobre el valor de una expresión.
Intuición sobre el valor de una expresión.
Evaluar expresiones con variables: problemas verbales.
Evaluar expresiones con una sola variable.
Evaluar expresiones con múltiples variables.
Evaluar expresiones con múltiples variables: fracciones y decimales.
Intuición sobre el valor de una expresión.
Evaluar expresiones con variables: problemas verbales.
Evaluar expresiones con potencias.
Autoevaluación sobre el valor numérico de una expresión algebraica.
Monomios
|
Para nombrar un monomio usaremos una letra mayúscula (lo normal es usar las letras: P, Q, R, S, ...) seguida de las variables que forman parte del monomio, entre paréntesis.
Por ejemplo:
a) 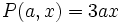 es un monomio de grado 2 y coeficiente 3.
es un monomio de grado 2 y coeficiente 3.
b) 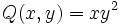 es un monomio de grado 3 y coeficiente 1.
es un monomio de grado 3 y coeficiente 1.
c) 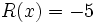 es un monomio de grado 0 y coeficiente -5.
es un monomio de grado 0 y coeficiente -5.
d) 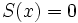 es el monomio nulo. Su grado es 0.
es el monomio nulo. Su grado es 0.
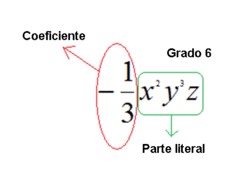
e) En la siguiente escena se puede observar el coeficiente y el grado de un monomio. En la parte superior se pueden cambiar los exponentes de las letras a, b, y x. Para cambiar el coeficiente del monomio modifica la casilla de abajo.
- Álgebra.
- Valor numérico de una expresión algebraica.
- Tipos de expresiones algebraicas.
- Monomios.
- Partes y grado de un monomio.
Monomios: Expresión general, coeficiente, parte literal y grado.
Aprende a calcular el grado relativo y absoluto de un monomio.
Nota: Al "grado absoluto" de un monomio se le llama simplemente "grado" del monomio.
Indica el coeficiente, la parte literal y el grado de los siguientes monomios: 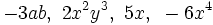
1) Indica cuáles de estas expresiones son monomios:
- a)
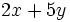 ; b)
; b) 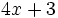 ; c)
; c)  ; d)
; d) 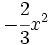 ;
;
- e)
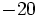 ; f)
; f) 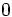 ; g)
; g) 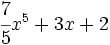
2) Escribe cinco expresiones que sean monomios.
3) Escribe el coeficiente y el grado de cada monomio:
- a)
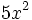 ; b)
; b) 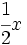 ; c)
; c) 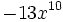 ; d)
; d) 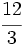 ; e)
; e) 
4) Escribe un monomio de coeficiente -2, otro de coeficiente 7 y otro de coeficiente 1/2.
5) Escribe un monomio de grado 2, otro de grado 1, otro de grado 0 y otro de grado 10.
6) Escribe un monomio de coeficiente -2 y grado 3.
7) Escribe un monomio tal que su coeficiente y su grado sean iguales.
8) Escribe un monomio que no tenga grado y otro que tenga grado cero.
9) Haz una tabla en la que se recojan el coeficiente, la parte literal y el grado de los siguientes monomios:
- a)
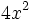 ; b)
; b) 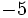 ; c)
; c) 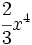 ; d)
; d) 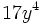 ; e)
; e) 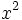
Actividades en la que aprenderás y practicarás a hallar los elementos y el grado de un monomio.
Ejercicios de autoevaluación sobre el grado y los elementos de un monomio.
Monomios semejantes
Son monomios semejantes aquellos que tienen la misma parte literal, es decir, aquellos en los que intervienen las mismas variables con los mismos exponentes.
Son monomios semejantes: 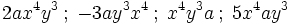
Las letras pueden aparecer en distinto orden ya que por la propiedad conmutativa las podemos reordenar.
Actividades en la que aprenderás y practicarás a hallar los elementos y el grado de un monomio. También practicaras con monomios semejantes y opuestos.
Aprende a distiguir cuando dos monomios son o no semejantes.
Aprende a distiguir cuando dos monomios son o no semejantes.
Aprende a distiguir cuando dos monomios son o no semejantes.
Monomios semejantes. Ejemplos.
Valor numérico de un monomio. Monomios constantes, monomios nulos y monomios semejantes. Ejemplos.
Encuentra los términos semejantes.
10) Indica cuáles de los siguientes monomios son semejantes:
11) Escribe tres monomios semejantes a 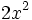 .
.
12) Escribe tres monomios semejantes a 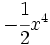 .
.
13) Escribe tres monomios semejantes a 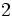 .
.
14) Escribe tres monomios semejantes a 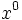 .
.
15) Escribe cinco monomios constantes.
16) Escribe cinco monomios nulos.
Monomios opuestos
Dos monomios se dicen opuestos si son semejantes y tienen coeficientes opuestos.
Calcula el opuesto de los siguientes monomios y luego súmalos:
- 33)
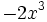 ; 34)
; 34) 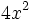 ; 35)
; 35) 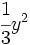 ; 36)
; 36) 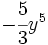
Valor numérico de un monomio
El valor numérico de un monomio es el número que se obtiene al sustituir las letras por ciertos números.
Con la notación que utilizamos para nombrar los monomios y que hemos visto anteriormente, resulta más sencillo hacer referencia al valor numérico de un monomio. El nombre que escogemos está acompañado de las variables del monomio, así que si queremos referirnos a un valor numérico en concreto no tenemos más que escribir el nombre del monomio cambiando las variables por el valor que corresponda. Fíjate cómo se hace en los siguientes ejemplos:
Halla el valor numérico de los siguientes monomios:
a) 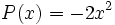 para x = 2.
para x = 2.
b) 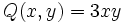 para x = 1 e y = -2.
para x = 1 e y = -2.
Solución:
a) 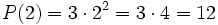
b) 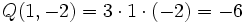
Ejemplo de cálculo del grado y del valor numérico de un monomio con varias variables.
Ejemplos de cálculo del valor numérico de un monomio.
Calcula el valor numérico de los siguientes monomios para los valores de las variables indicados:
- 17)
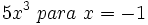
- 18)
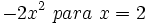
- 19)
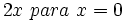
- 20)
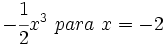
- 21)
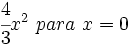
Polinomios
|
Para nombrar un polinomio usaremos una letra mayúscula (lo normal es usar las letras: P, Q, R, S, ...) seguida de las variables que forman parte del polinomio, entre paréntesis.
Por ejemplo:
a) El polinomio 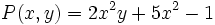 está en forma reducida y es un trinomio de grado 3.
está en forma reducida y es un trinomio de grado 3.
b) El polinomio 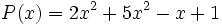 no está en forma reducida. Su forma reducida es
no está en forma reducida. Su forma reducida es 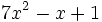 . Es de grado 2.
. Es de grado 2.
c) Los polinomios constantes, como por ejemplo 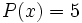 , tienen grado 1. Sin embargo, el polinomio nulo,
, tienen grado 1. Sin embargo, el polinomio nulo, 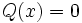 , tiene grado cero.
, tiene grado cero.
d) Los polinomios 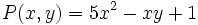 y
y 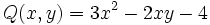 son semejantes.
son semejantes.
e) Los polinomios 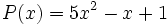 y
y 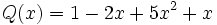 son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
Tutorial en el que se dan las definiciones básicas del álgebra: expresión algebraica, monomios, polinomios, grado, término independiente, coeficientes...
Polinomios. Grado de un polinomio. Ejemplos.
Polinomios. Grado de un polinomio. Ejemplos.
Aprende a calcular el grado relativo y absoluto de un polinomio.
Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio.
Aprende a calcular el grado relativo y absoluto de un monomio y de un polinomio.
Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio.
Polinomios: términos y tipos de polinomios. Polinomios nulos.
Forma reducida de un polinomio. Grado. Polinomios iguales y semejantes.
- Polinomios ordenados, completos / incompletos, homogéneos / heterogéneos.
- Valor numérico de un polinomio.
Polinomios. Monomios. Grado y término independiente de un polinomio.
1) Indica de qué tipo son los polinomios siguientes, atendiendo al número de términos que tienen:
- a)
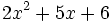
- b)
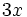
- c)
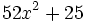
- d)
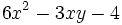
- e)
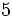
- f)
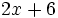
2) Expresa en forma reducida los siguientes polinomios:
- a)
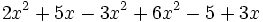
- b)
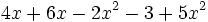
- c)
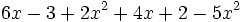
- d)
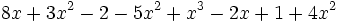
3) Indica el grado de cada polinomio:
- a)
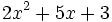 ; b)
; b) 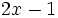 ; c)
; c) 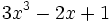
- d)
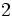 ; e)
; e) 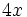 ; f)
; f) 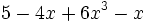
- g)
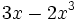 ; h)
; h) 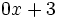 ; i)
; i) 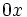
4) Indica cuáles de estos polinomios son iguales:
- a)
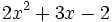 ; b)
; b) 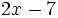 ; c)
; c) 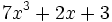 ; d)
; d) 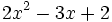
- e)
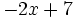 ; f)
; f) 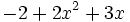 ; g)
; g) 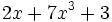 ; h)
; h) 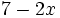
- i)
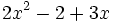 ; j)
; j) 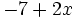 ; k)
; k) 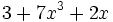 ; l)
; l) 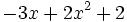
5) Indica cuáles de estos polinomios son semejantes entre sí:
- a)
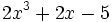 ; b)
; b) 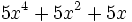 ; c)
; c) 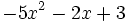
- d)
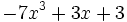 ; e)
; e) 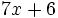 ; f)
; f) 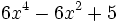
- g)
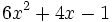 ; h)
; h) 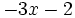
6) Ordena, tanto de forma creciente como decreciente, e indica el grado de los siguientes polinomios:
- a)
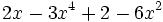
- b)
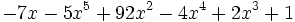
- c)
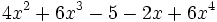
- d)
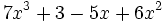
- e)
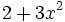
- f)
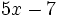
7) Clasificar polinomios en homogéneos/heterogéneos.
- a)
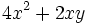
- b)
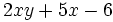
- c)
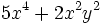
- d)
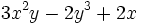
- e)
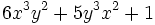
- f)
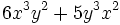
- g) 5x3 − 6y3
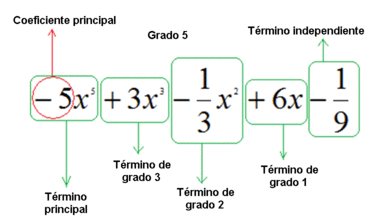
Dado el polinomio 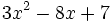 , identifica sus términos junto con el coeficiente y exponente de cada uno de ellos.
, identifica sus términos junto con el coeficiente y exponente de cada uno de ellos.
Escribe un polinomio que exprese el valor de "p" billetes de 20 pesos, "q" monedas de 10 pesos y "r" monedas de 5 pesos.
Elementos y grado de un polinomio.
Expresiones algebraicas: monomios y polinomios.
- Actividad en la que deberás encontrar la expresión polinómica adecuada para cada situación.
- Actividad en la que deberás construir un polinomio conocida cierta información sobre su grado y los coeficientes de sus términos.
- Actividad en la que deberás encontrar el valor de algún coeficiente de un polinomio.
- Actividad en la que aprenderás a escribir polinomios en su forma usual.
- Actividad en la que deberás decir cual es el coeficiente de cada grado de un polinomio.
Actividad sobre polinomios.
Valor numérico y raíces de un polinomio
Si en un polinomio se sustituyen las letras por números y se realiza la operación indicada se obtiene un número que es el valor númerico del polinomio para los valores de las letras dados.
Si trabajamos con una sola variable, dado un polinomio P(x), el valor numérico de dicho polinomio para x=a es el número que se obtiene al sustituir la x por a y efectuar las operaciones indicadas. A ese número se le llama P(a).
Por ejemplo:
Dado 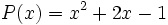 , el valor númerico de dicho polinomio para
, el valor númerico de dicho polinomio para  es
es 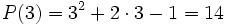
Valor numérico de un polinomio.
Aprende a calcular el valor numérico de un polinomio
Valor numérico de un polinomio.
Halla el valor numérico del polinomio 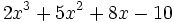 cuando
cuando 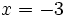
Dado el polinomio 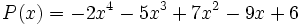 , determina
, determina 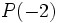 .
.
Halla el valor numérico del polinomio 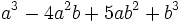 cuando
cuando 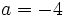 y
y 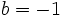
8) Calcula el valor numérico de los siguientes polinomios para el valor de la variable indicado:
- a)
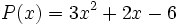 para
para 
- b)
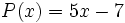 para
para 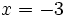
- c)
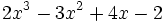 para
para 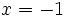
- d)
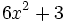 para
para 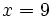
- e)
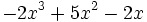 para
para 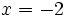
Evalúa el polinomio 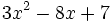 en
en  .
.
Distintas situaciones en las que se hace uso del valor numérico de un polinomio. Por ejemplo, cuando se expresa un número en un sistema de numeración de una determinada base.
Actividades en las que deberás calcular el valor numérico de un polinomio.
Un número se dice que es una raíz de un polinomio si el valor numérico del polinomio para dicho número es cero.
Esto es,  es una raíz de un polinomio
es una raíz de un polinomio  si y solo si
si y solo si 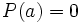 .
.
O dicho de otra manera, las raíces de un polinomio  son las soluciones de la ecuación
son las soluciones de la ecuación 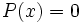 .
.
Veamos como el número 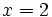 es una raíz del polinomio
es una raíz del polinomio 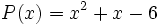 .
.
En efecto, al sustituir la x por 2, el valor numérico del polinomio es cero: 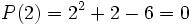
|
Actividad: Valor numérico y raíces de un polinomio Calcula el valor numérico del polinomio
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
De a) y c) se deduce que x=2 y x=1 son raíces del polinomio. Prueba a introducir lo siguiente: roots x^2-3x+2 |
Operaciones con monomios y polinomios
Suma y resta de monomios
Procedimiento
Para sumar o restar dos monomios tienen que ser semejantes. La suma o resta es otro monomio semejante a ellos que tiene por coeficiente la suma o diferencia, según el caso, de los coeficientes.
Suma y resta de monomios. Monomios opuestos.
Aprende a sumar y restar monomios
Aprende a sumar y restar monomios
Aprende a sumar y restar monomios
Agrupa (reduce) términos semejantes:
a) 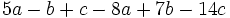
b) 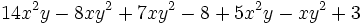
Reduce:
a) 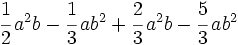
b) 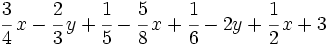
Realiza las siguientes sumas y restas de monomios:
- 22)
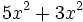 ; 23)
; 23) 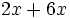 ; 24)
; 24) 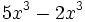
- 25)
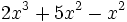 ; 26)
; 26) 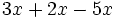 ; 27)
; 27) 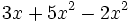
- 28)
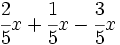 ; 29)
; 29)  ; 30)
; 30) 
- 31)
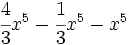 ; 32)
; 32) 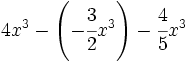
Actividades en la que aprenderás y practicarás a sumar y restar monomios.
Actividades para practicar la suma y resta de monomios.
Actividades para practicar la suma y resta de monomios.
Actividades para practicar la suma y resta de monomios.
Reducción de polinomios
Procedimiento
Para reducir un polinomio sumaremos o restaremos los monomios semejantes que aparezcan en su expresión. Los monomios resultantes se suelen ordenar de mayor a menor grado.
Aprende a reducir polinomios con Chuck Norris.
Reduce: 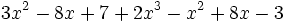
Reduce: 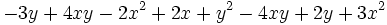
Reduce: 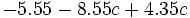
Reducción de polinomios.
Reducción de polinomios con coeficientes racionales.
Suma y resta de polinomios
Procedimiento
Para sumar o restar polinomios, sumaremos o restaremos los monomios semejantes de ambos.
Aprende a sumar y restar polinomios
En este tutorial se explica la suma y resta de polinomios comenzando con algunas definiciones básicas y terminando con ejemplos.
Aprende a sumar polinomios
Aprende a restar polinomios
Suma y resta de polinomios en una variable. Ejemplos.
Suma de polinomios. Ejemplos.
Propiedades de la suma de polinomios: conmutativa y asociativa.
Propiedades de la suma de polinomios: Elemento neutro y opuesto.
Resta de polinomios. Equivalencias fundamentales.
Suma y resta de polinomios.
Calcula la suma: 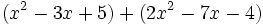
Calcula la suma: 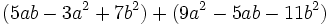
Calcula la resta: 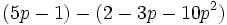
Calcula la resta: 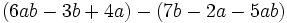
Calcula:
a) 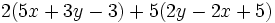 b)
b) 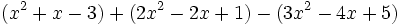
Simplifica: 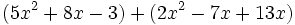
Simplifica: 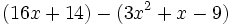
Resta 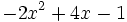 de
de 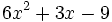 .
.
Simplifica: 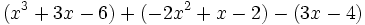
Simplifica: 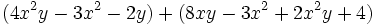
Simplifica: 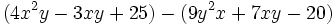
Resta 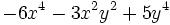 de
de 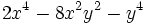 .
.
Encuentra el error cometido en la resta que se muestra en el video.
1) Ordena los polinomios y realiza las sumas que se indican:
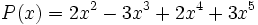 ;
; 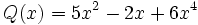
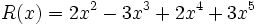 ;
; 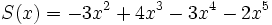
1a) P(x) + Q(x)
1b) P(x) + R(x)
1c) P(x) + S(x)
Dados los siguientes polinomios, realiza las sumas que se indican:
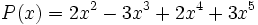 ;
; 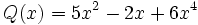
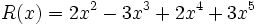 ;
; 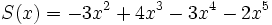
1d) Q(x) + S(x)
1e) R(x) + S(x)
1f) Q(x) + R(x)
2) Sumas los siguientes polinomios y compara el grado del polinomio suma con el grado de los polinomios sumandos.
3a) Escribe opuestos de los siguientes polinomios:
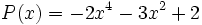 ;
; 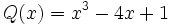
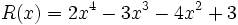 ;
; 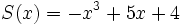
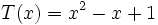 ;
; 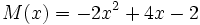
3b) Suma cada uno de los polinomios del apartado anterior con su opuesto.
3c) Calcula un polinomio A(x) tal que 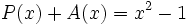 , siendo
, siendo 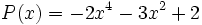 .
.
Dados los siguientes polinomios:
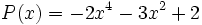 ;
; 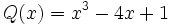
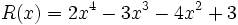 ;
; 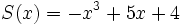
3d) Calcula un polinomio B(x) tal que 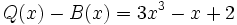 .
.
3e) Calcula un polinomio C(x) tal que 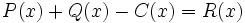 .
.
3f) Calcula un polinomio D(x) tal que 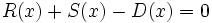 .
.
Dados los polinomios:
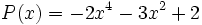 ;
; 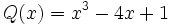
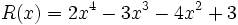 ;
; 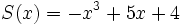
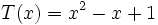 ;
; 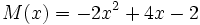
4a) Calcula P(x) - Q(x).
4b) Calcula P(x) - R(x).
4c) Calcula [P(x) + Q(x)]-[R(x) + S(x)]
4d) Calcula [P(x) + S(x)]-[Q(x) + R(x)]
4e) Calcula T(x) + M(x)
4f) Calcula T(x) - M(x)
5) ¿Qué polinomio se ha de restar al polinomio 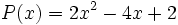 para obtener el polinomio
para obtener el polinomio 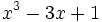 ?
?
6) Dados los polinomios
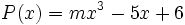 ;
; 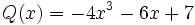
calcula el valor de  sabiendo que
sabiendo que 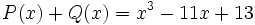 .
.
7) Escribe dos polinomios de tercer grado de tal modo que su suma se el polinomio nulo.
8) Escribe dos polinomios reducidos de segundo grado y comprueba con ellos la conmutatividad de la suma.
9) Dado el polinomio 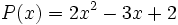 , escribe su opuesto, -P(x). Calcula los valores numéricos de P(x) y -P(x) para x = 0, x = 1 y x = 2, y comprueba comprueba que son números opuestos.
, escribe su opuesto, -P(x). Calcula los valores numéricos de P(x) y -P(x) para x = 0, x = 1 y x = 2, y comprueba comprueba que son números opuestos.
10) ¿Qué polinomio tienes que sumar con 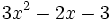 para que la suma sea 5x^3-6x?
para que la suma sea 5x^3-6x?
11) Dado el polinomio 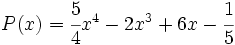 , halla otro polinomio Q(x) tal que
, halla otro polinomio Q(x) tal que 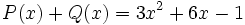 .
.
Dados los polinomios
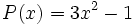 ;
; 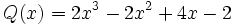
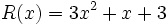 ;
; 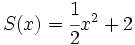
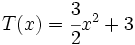 ;
; 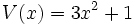
12a) Calcula P(x) + Q(x).
12b) Calcula P(x) - V(x).
12c) Calcula P(x) + R(x).
12d) Calcula P(x) - R(x).
12e) Calcula S(x) + T(x) + V(x).
12f) Calcula S(x) - T(x) + V(x).
13) Dados los polinomios
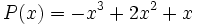 ;
; 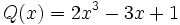
calcula el polinomio M(x) tal que P(x) + M(x) = Q(x).
17) La diferencia de dos polinomios es:
Calcula  sabiendo que
sabiendo que 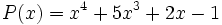 .
.
18) ¿Qué polinomio hay que sumar al polinomio 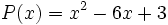 para obtener el polinomio opuesto de
para obtener el polinomio opuesto de 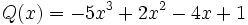 ?
?
19) Dados los polinomios:
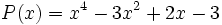 ;
; 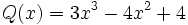 ;
; 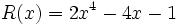
- 19a) Calcula P(x) + Q(x) - R(x)
- 19b) Calcula P(x) + R(x) - Q(x)
- 19c) Calcula Q(x) + R(x) - P(x)
- 19d) Calcula P(x) + Q(x) + R(x)
14) Escribe dos polinomios cualesquiera y súmalos. Contesta:
- 14a) ¿Es mayor el grado de los sumandos o el de la suma? ¿Es igual? ¿Es menor?
- 14b) ¿Puede en algún caso ser menor el grado de la suma que el de los sumandos? ¿Cuándo? Justifícalo con ejemplos.
15) ¿Qué puedes decir del grado de la diferencia de dos polinomios?
16) escribe dos polinomios de tercer grado de modo que su suma se el polinomio 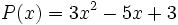 .
.
Determina el valor de "m" y "n" sabiendo que 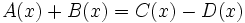 , en los siguientes casos:
, en los siguientes casos:
Actividades para aprender y practicar la suma y resta de polinomios.
Ejercicios para practicar la suma y resta de polinomios.
Suma de polinomios.
Resta de polinomios.
Suma y resta de polinomios.
Suma y resta de polinomios con dos variables.
Suma y resta de polinomios con dos variables.
Suma y resta de polinomios con dos variables: encuentra el error.
Suma de polinomios.
Resta de polinomios.
Ejercicios de autoevaluación sobre suma y resta de polinomios.
Ejercicios propuestos
|
Ejercicios propuestos: Expresiones algebraicas. |
Multiplicación de monomios
Procedimiento
Para multiplicar monomios, se multiplican los coeficientes de cada monomio y las potencias con la misma base se agrupan y se multiplican.
Recordemos que: para multiplicar potencias de la misma base se deja la misma base y se suman los exponentes.
Multiplicación de monomios. Ejemplos.
Haz las siguientes multiplicaciones de monomios:
- a)
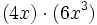
- b)
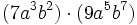
- c)
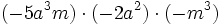
Haz las siguientes multiplicaciones de monomios:
- a)
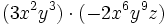
- b)
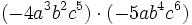
- c)
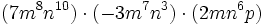
- d)
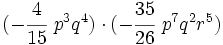
Haz las siguientes multiplicaciones de monomios:
- a)
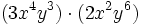
- b)
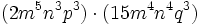
- c)
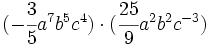
Multiplica los siguientes monomios:
- 37)
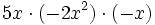 ; 38)
; 38) 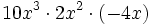 ; 39)
; 39) 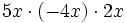
- 40)
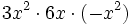 ; 41)
; 41) 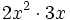 ; 42)
; 42) 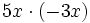
- 43)
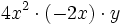 ; 44)
; 44) 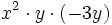
Multiplica los siguientes monomios:
- 45)
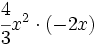 ; 46)
; 46) 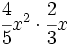 ; 47)
; 47) 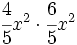
- 48)
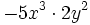 ; 49)
; 49) 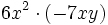 ; 50)
; 50) 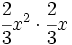
- 51)
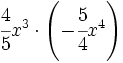 ; 52)
; 52) 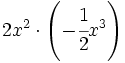 ; 53)
; 53) 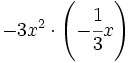
Expresa en forma de un monomio el área de un rectángulo que mide 4y de largo y 2y de ancho.
Expresa en forma de un monomio el área de un rectángulo que mide 4xy de largo y 2y de ancho.
Averigua el valor de "a" y "b" sabiendo que 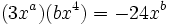 .
.
Actividades en la que aprenderás y practicarás a multiplicar monomios.
Actividades para practicar la multiplicación de monomios.
Multiplicación de monomios.
Multiplicación de monomios.
Multiplicación de un monomio por un polinomio
Procedimiento
Para multiplicar un monomio por un polinomio, se aplica la propiedad distributiva, es decir, se multiplica el monomio por cada término del polinomio y se suman los resultados.
Aprende a multiplicar un monomio por un polinomio
Cómo se multiplica un polinomio por un monomio.
Multiplica y reduce:
- a)
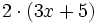
- b)
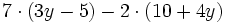
Expresa el área de la figura dada en el video como un trinomio.
Multiplica: 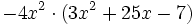
Averigua el valor de "c", "d" y "f" sabiendo que 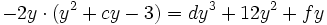
Multiplica:
- a)
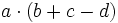
- b)
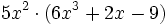
- c)
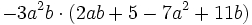
- d)
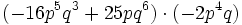
Haz las siguientes multiplicaciones de monomios:
- a)
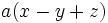
- b)
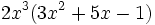
- c)
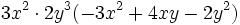
Calcula 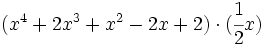
Calcula:
- 1c)
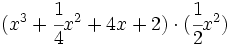
- 1d)
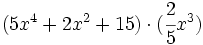
Actividades para aprender y practicar la multiplicación de un monomio por un polinomio.
Multiplicación de un número por un polinomio.
Multiplicación de monomios por polinomios.
Multiplicación de monomios por polinomios.
Multiplicación de monomios por polinomios.
División de monomios
Entenderemos la división entre monomios como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base.
Aprende a dividir monomios
Divide:
- a)
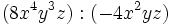
- b)
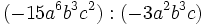
- c)
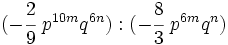
Divide los siguientes monomios:
- 54)
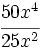 ; 55)
; 55) 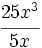 ; 56)
; 56) 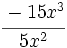 ; 57)
; 57) 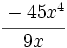
- 58)
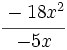 ; 59)
; 59) 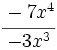 ; 60)
; 60) 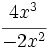 ; 61)
; 61) 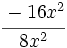
- 62)
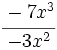 ; 63)
; 63) 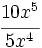 ; 64)
; 64) 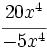 ; 65)
; 65) 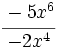
Cómo se multiplican y dividen monomios. Ejemplos.
Ejercicios propuestos
Operaciones con monomios:
- a)
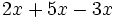
- b)
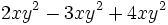
- c)
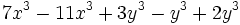
- d)
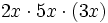
- e)
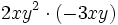
- f)
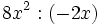
- g)
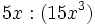
Ejercicios de autoevaluación sobre operaciones con monomios.
¿Qué expresiones son equivalentes con 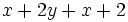 ?
?
Elige todas las opciones correctas:
- a)
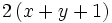
- b)
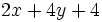
- c) Ninguna de las anteriores.
|
Ejercicios propuestos: Operaciones con monomios y polinomios |
Actividades
Ejercicios para practicar con expresiones algebraicas y monomios.
Teoría y actividades sobre expresiones algebraicas: monomios, polinomios, operaciones.
Ejercicios de autoevaluación sobre expresiones algebraicas y valor numérico.
Ejercicios resueltos sobre monomios.
Ejercicios de autoevaluación sobre monomios.
Apéndice
Introducción al análisis dimensional.
Otro ejemplo de análisis dimensional.
Elige la respuesta adecuada (ver video).
Elige la respuesta adecuada (ver video).
Supervivencia de una ardilla.
Coste de la gasolina para un viaje.
Convertir unidades de longitud.
Convertir unidades: dosis medicinal.
Autoevaluación sobre análisis dimensional.
Problemas de tasas.
Problemas de varais unidades.
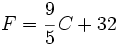
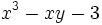
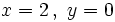
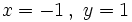
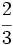
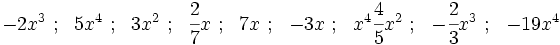
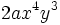 y
y 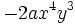
 en los casos:
en los casos:
 b)
b) 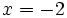 c)
c)