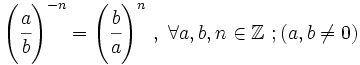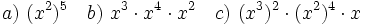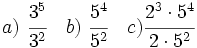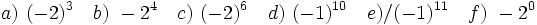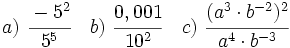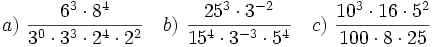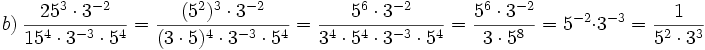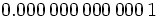Potencias (3ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 28)
Potencias de números racionales
Vamos a estudiar las potencias cuya base es un número racional y cuyo exponente es un número entero. Las potencias cuya base es un número racional se definen y tiene las mismas propiedades que las que tienen como base un número entero. En el siguiente enlace puedes repasar estas últimas.
Ver: Potencias de números enteros
Definición de potencia de un número racional
La definición de potencia de números racionales es la misma que la de números enteros.
Una potencia es un modo abreviado de escribir un producto de un número por sí mismo:
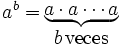 (Se lee: "
(Se lee: " elevado a
elevado a  ")
")- El número
 se llama base. Es el número que se multiplica por sí mismo.
se llama base. Es el número que se multiplica por sí mismo.
- El número
 se llama exponente. Es el número que indica las veces que la base aparece como factor.
se llama exponente. Es el número que indica las veces que la base aparece como factor.
- Por convenio, se establece que:
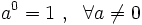 .
.
- Cuando el exponente de una potencia es el número 1 no se pone exponente, basta con poner el número de la base.
Cómo se leen las potencias:
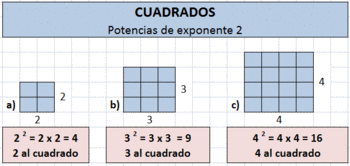
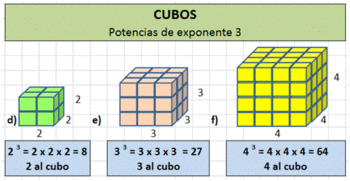
Cuando el exponente es 2 se dice "elevado al cuadrado", cuando el exponente es 3 se dice "elevado al cubo". En los demás casos se dice "elevado a la cuarta, quinta, sexta... potencia".
- Breve repaso de las potencias de base entera y exponente natural.
- Potencias de base racional y exponente natural.
- Potencias de exponente 0 y 1.
Cómo se calcula la potencia de una fracción. Ejemplos.
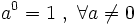 . Ejemplos.
. Ejemplos.
- Escribe en forma de potencia los siguientes productos:
- 1)
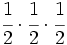
- 2)
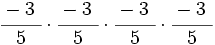
- 3)
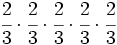
- Escribe en forma de una única potencia:
- 4)
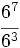 ; 5)
; 5) 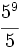 ; 6)
; 6) 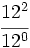
- 7)
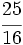 ; 8)
; 8) 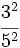 ; 9)
; 9) 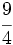 ; 10)
; 10) 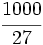
Potencias de base negativa
Signo de la potencia
Dependiendo del signo de la base tenemos dos posibilidades:
- Base positiva: Al elevar un número positivo a una potencia, el resultado es positivo.
- Base negativa: Al elevar un número negativo a una potencia, el resultado es positivo si el exponente es par y negativo si es impar.
Cómo se calcula el signo de la potencia de una fracción.
Potencias de exponente entero negativo
Se define la potencia de exponente negativo como:

Como consecuencia:
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos.
 . Ejemplos.
. Ejemplos.
Exponentes negativos. Ejemplos.
Razonando sobre el por qué de la definición de los exponentes negativos.
Simplifica:
- a)
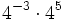
- b)
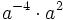
- c)
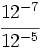
- d)
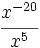
Simplifica:
- a)
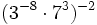
- b)
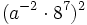
- c)
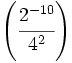
Halla el valor de:
11) 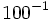 ; 12)
; 12) 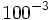 ; 13)
; 13) 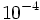 ; 14)
; 14) 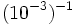
15) 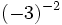 ; 16)
; 16) 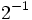 ; 17)
; 17) 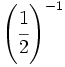 ; 18)
; 18) 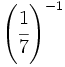 ; 19)
; 19) 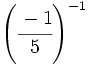
Potencias de exponente negativo.
Actividades sobre potencias de exponente negativo.
Calcula las siguientes potencias y comprueba los resultados en la escena siguiente:
a) 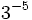 b)
b) 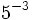 c)
c) 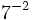 d)
d) 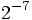
Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba.
Potencias de exponente negativo.
Multiplica y divide potencias (exponentes enteros).
Potencias de productos y cocientes (exponentes enteros)
Potencias de exponentes enteros.
Pulsa el botón "EJERCICIO" y lee atentamente el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien.
Ejercicios de autoevaluación sobre potencias de exponente negativo.
Propiedades de las potencias de números racionales
Las potencias con números racionales cumplen las mismas propiedades que las potencias de números enteros.
Ver: Propiedades de las potencias de números enteros
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
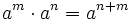
- 2. Cociente de potencias de la misma base:
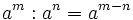
- 3. Potencia de un producto:
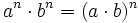
- 4. Potencia de un cociente:
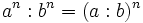
- 5. Potencia de otra potencia:
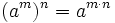
Tutorial muy completo que explica las propiedades básicas de las potencias con ejemplos resueltos sencillos y alguno más complejo.
- Potencias de exponente entero de números racionales.
- Propiedades.
- Ejemplos
Producto de potencias de fracciones con la misma base. Ejemplos.
Cociente de potencias de fracciones con la misma base. Ejemplos.
Potencia de otra potencia de una fracción. Ejemplos.
Potencia de un producto de fracciones. Ejemplos.
Producto de potencias de la misma base: 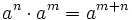 . Ejemplos.
. Ejemplos.
Cociente de potencias de la misma base: 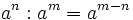 . Ejemplos.
. Ejemplos.
Potencia de otra potencia: 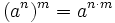 . Ejemplos.
. Ejemplos.
Potencia de un producto: 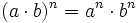 . Ejemplos.
. Ejemplos.
Potencia de un cociente: 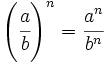 . Ejemplos.
. Ejemplos.
- Potencias de exponente 1 y 0.
- Producto y cociente de potencias de la misma base.
- Potencia de un producto y de un cociente.
- Potencia de otra potencia.
- Ejemplos.
- Potencias de base negativa.
- Potencias de exponente negativo.
- Ejemplos.
Cálculos con potencias de exponente positivo.
Cálculos con potencias de exponente negativo.
Simplificaciones de operaciones con potencias.
Cálculos con potencias de fracciones:
Calcula:
20) 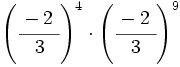 ; 21)
; 21) 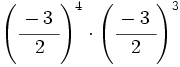 ; 22)
; 22) 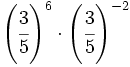
23) 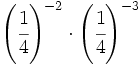 ; 24)
; 24) 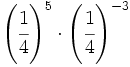 ; 25)
; 25) 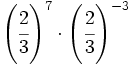
26)  ; 27)
; 27) 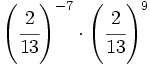 ; 28)
; 28) 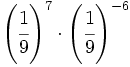
Calcula:
29) 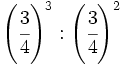 ; 30)
; 30)  ; 31)
; 31) 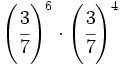
32) 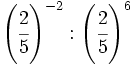 ; 33)
; 33) 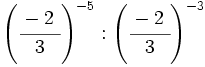 ; 34)
; 34) 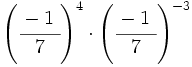
Calcula:
- 35)
![\left[ \left( \cfrac{-3~}{7} \right)^2 \right]^3](/wikipedia/images/math/0/d/5/0d5ecdfc87205ac8f368d6a70a5e1225.png) ; 36)
; 36) ![\left[ \left( \cfrac{2}{3} \right)^3 \right]^5](/wikipedia/images/math/2/9/c/29cf02b990eee91e9f5267cd7ae27ab8.png) ; 37)
; 37) ![\left[ \left( \cfrac{3}{4} \right)^2 \right]^4](/wikipedia/images/math/8/5/9/85905a10045ecdadf0d87cb496b46fd4.png)
- 38)
![\left[ \left( \cfrac{2}{5} \right)^3 \right]^2](/wikipedia/images/math/7/7/c/77ccd9469ab61459b42b5c42c31b6a03.png) ; 39)
; 39) ![\left[ \left( \cfrac{2}{3} \right)^{-2} \right]^{-3}](/wikipedia/images/math/7/1/7/717d66168670db7c17604eed1ecc5697.png) ; 40)
; 40) ![\left[ \left( \cfrac{3}{5} \right)^{-2} \right]^{-7}](/wikipedia/images/math/7/d/5/7d5523f771792c7a7444cc796d7a29e6.png)
- 41)
![\left[ \left( \cfrac{-3~}{4} \right)^{-2} \right]^{-5}](/wikipedia/images/math/d/e/2/de20c03afc7ad82625777cdcf282c409.png) ; 42)
; 42) ![\left[ \left( \cfrac{-2~}{7} \right)^3 \right]^{-2}](/wikipedia/images/math/d/8/f/d8f17a4b8bd520d1104f16e3bbe69742.png) ; 43)
; 43) ![\left[ \left( \cfrac{-2~}{7} \right)^{-1} \right]^3](/wikipedia/images/math/d/9/9/d996341203e6a65e266433c712564961.png)
- 44)
![\left[ \left( \cfrac{2}{5} \right)^{-3} \right]^{-2}](/wikipedia/images/math/e/2/b/e2b4f1793a567fb108f0a0c11c815bcb.png) ; 45)
; 45) ![\left[ \left( \cfrac{-2~}{5} \right)^{-3} \right]^{-2}](/wikipedia/images/math/1/5/4/154452bc7b4e3830e7474ee197167695.png) ; 46)
; 46) ![\left[ \left( \cfrac{-1~}{8} \right)^{-2} \right]^{-3}](/wikipedia/images/math/d/f/7/df755b98eccd3553b490053829676d47.png)
Escribe como varias potencias:
- 47)
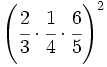
- 48)
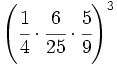
- 49)
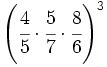
- 50)
![\left[ \cfrac{1}{3} \cdot \left( \cfrac{-2~}{5} \right) \cdot \left( \cfrac{-2~}{2} \right) \right]^2](/wikipedia/images/math/5/b/1/5b1a30cdfd3990559ce215699a00c2e3.png)
- 51)
![\left[ \cfrac{2}{3} \cdot \left( \cfrac{-5~}{4} \right) \cdot \cfrac{8}{5} \cdot \left( \cfrac{-5~}{2} \right) \right]^{-3}](/wikipedia/images/math/4/0/6/4066e6d3414c3e8d17a4b0e6837cad6a.png)
Escribe como una sola potencia:
- 52)
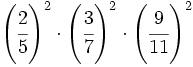
- 53)
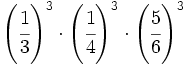
- 55)
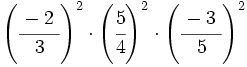
- 56)
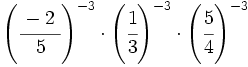
- 57)
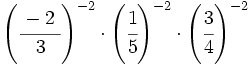
- 58)
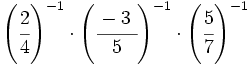
Simplifica:
- a)
![\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3](/wikipedia/images/math/f/e/c/fec21991837955f9b9d945d4600cba18.png)
- b)
![\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2}](/wikipedia/images/math/e/5/1/e5178ed20376c4ef7f07ca88d5d43975.png)
Simplifica 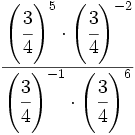
Simplifica: ![\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2](/wikipedia/images/math/6/9/1/6911b07dbbc54e802f87f7498ab77b09.png)
Cálculos con potencias dentro de fracciones:
Calcula:
- 59)
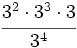
- 60)
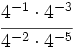
- 61)
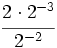
- 62)
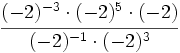
Calcula:
- 63)
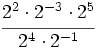
- 64)
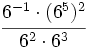
- 65)
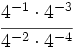
- 66)
![\cfrac{(-3)^{-2} \cdot (-3)^{-3}}{\left[ (-3)^2 \right]^{-2}}\;](/wikipedia/images/math/5/e/b/5eb0dbb75ab3ac5de8238f112e4d893f.png)
Simplifica: 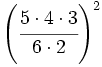
Simplifica: ![\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3](/wikipedia/images/math/7/1/b/71b5b62cb54ed835ba335fdbca4de909.png)
Simplifica: 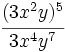
Simplifica: 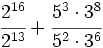
Simplifica y expresa la solución como una única potencia:
a) 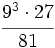
b) 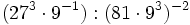
c) 
d) 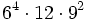
e) a) 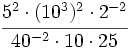
Simplifica y expresa la solución como una única potencia:
a) 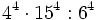
b) 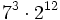
c) 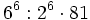
d) 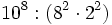
e) 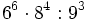
f) 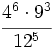
Simplifica:
- a)
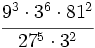
- b)
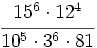
Simplifica:
- a)
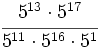
- b)
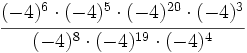
- c)
![\left[ \cfrac{( 2^3 \cdot 2^6)^{-2} \cdot (3^4)^3 \cdot 3 }{( 2^6 \cdot 2^{10})^{-1}\cdot (3^6 \cdot 3^2 \cdot 3^5)}\right]^{10}](/wikipedia/images/math/c/8/5/c85c926802bdbb7a51ef34eb65c6dda7.png)
Cálculos de diversos tipos:
Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa.
Exponente positivo:
- a)
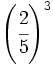 ; b)
; b)  ; c)
; c)  ; d)
; d) 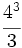 ; e)
; e) 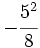
Exponente negativo:
- f)
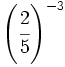 ; g)
; g) 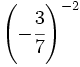 ; h)
; h) 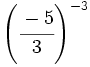 ; i)
; i) 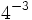 ; j)
; j) 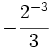
Operaciones combinadas:
- k)
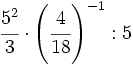 ; l)
; l) 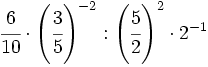
Ejercicios
Actividades en las que podrás aprender a operar con potencias y a aplicar sus propiedades.
Pulsa el botón EJERCICIO para ver el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena (de forma que la base no sea una potencia) y pulsas el botón SOLUCIÓN para ver si lo has hecho bien.
- Potencia de números racionales con exponente entero. Potencia de exponente negativo. Propiedades de las potencias.
- Ejercicios resueltos.
Operaciones con potencias de racionales con exponente entero.
Ejercicios de autoevaluación sobre operaciones con potencias de números racionales.
Ejercicios resueltos
|
Actividades: Potencias
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
|
Ejercicios: Operaciones con potencias Calcula utilizando las propiedades de las potencias:
Solución: 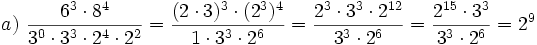
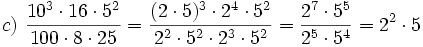 |
(Pág. 28)
Ejercicios resueltos
Reducir a una sola potencia:
- a)
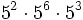 b)
b) 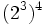
- c)
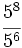 d)
d) 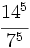
- e)
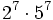 f)
f) 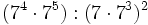
a)
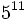 ; b)
; b) 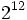 ; c)
; c) 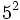 ; d)
; d) 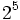 ; e)
; e) 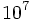 ; f)
; f) 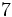 ;
;(Pág. 29)
Ejercicios resueltos
1. Expresa como potencia de base 10:
2. Simplifica:
- a)
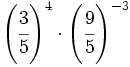 b)
b) ![\left[ \left( \cfrac{5}{2} \right)^{-2} \right]^{-3}](/wikipedia/images/math/d/9/b/d9bc495e338d2e6b51f9ae0e2b7467c8.png) c)
c) 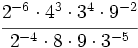
1. 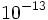
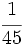 ; b)
; b) 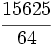 ; c)
; c) 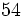
Ejercicios propuestos
|
Ejercicios propuestos: Potencias |