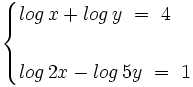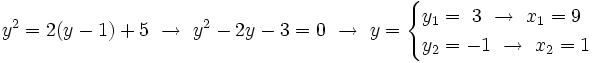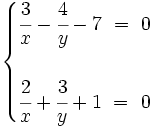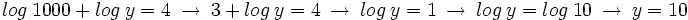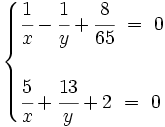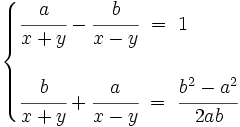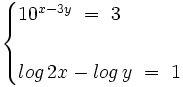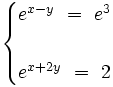Sistemas de ecuaciones (1ºBS)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Calculadora |
Tabla de contenidos |
Sistemas de ecuaciones
(pág. 81)
- Un sistema de n ecuaciones con m incógnitas o simplemente, sistema nxm, es la agrupación de n ecuaciones con m incógnitas.
- Se llama solución de un sistema nxm a cualquier conjunto de m valores (uno de cada incógnita) que sea solución de todas las ecuaciones a la vez.
- Resolver un sistema es hallar todas sus soluciones.
- Dos sistemas son equivalentes si tienen las mismas soluciones.
- Si las ecuaciones que forman el sistema están formadas por expresiones polinómicas de primer grado, el sistema se dice que es lineal. En caso contrario diremos que es no lineal.
Qué es un sistema de ecuaciones no lineales.
Clasificación de los sistemas atendiendo al número de soluciones
- Un sistema es compatible si tiene solución e incompatible si no la tiene.
- Un sistema es determinado si tiene un número finito de soluciones e indeterminado si tiene infinitas soluciones.
- Usaremos las siguientes siglas para abreviar:
- S.C.D. : Sistema Compatible Determinado (un número finito de soluciones)
- S.C.I. : Sistema Compatible Indeterminado (infinitas soluciones)
- S.I. : Sistema Incompatible (sin solución)
Métodos de resolución de sistemas
(pág. 81)
Vamos a ver tres métodos para resolver un sistema de ecuaciones: sustitución, igualación y reducción. Puedes recordar estos métodos de cursos anteriores: Métodos de resolución de sistemas (3ºESO Académicas)
Método de sustitución
El método de sustitución consiste en despejar una incógnita en una de las ecuaciones y sustituir en las otras:
- En el caso de sistemas 2x2, la ecuación sustituida, que se queda con una sola incógnita, se resuelve, lo que permite averiguar esa incógnita. Finalmente, el valor de la otra incógnita se obtiene sustituyendo en la expresión que obtuvimos al despejar en el paso previo.
- En el caso de sistemas de más de 2 incógnitas hay que repetir el proceso hasta quedarse con una sola ecuación con una incógnita. Una vez hallada ésta, se sustituye su valor en la expresión que obtuvimos al despejar, repitiendo estos pasos hasta tener todas las soluciones.
Ejercicio resuelto: Método de sustitución
Resuelve por el método de sustitución el siguiente sistema:
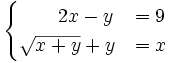
Despejamos la "y" en la primera ecuación:
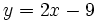 [1]
[1]Sustituimos esta expresión de la "y" en la segunda ecuación:
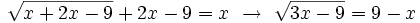
Elevamos al cuadrado los dos miembros de la ecuación para quitar el símbolo radical:
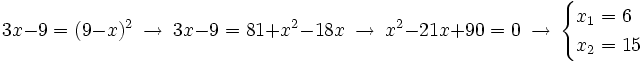
Para hallar la incógnita "y", sustituimos los valores de "x" en la ecuación [1]:
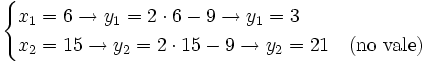
Comprobadas las soluciones en el sistema de partida, sólo resulta válida la primera solución.
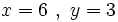
Ejercicio de aplicación del método de sustitución a la resolución de sistemas no lineales.
Resuelve:
Método de igualación (sistemas 2x2)
Consiste en despejar la misma incógnita en las dos ecuaciones e igualar las expresiones resultantes. Así, nos queda una ecuación con una sola incógnita. Esta se resuelve y permite averiguar dicha incógnita. Finalmente, el valor de la otra incógnita se obtiene sustituyendo el valor obtenido.
Ejemplo: Método de igualación
Resuelve por el método de igualación el siguiente sistema:
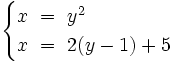
Como ya tenemos despejada la x\; en ambas ecuaciones, igualamos ambas expresiones:
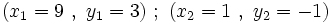
Resuelve por el método de igualación (previo cambio de variable):
Método de reducción
- Para sistemas 2x2, el método de reducción consiste en obtener ecuaciones equivalentes a las de partida (multiplicándolas por un número, si fuera necesario), de manera que al sumarlas, se obtenga una ecuación en la que se ha eliminado una de las incógnitas. Así, nos queda una ecuación con una sola incógnita, que se resuelve, permitiendo averiguar dicha incógnita. Finalmente, el valor de la otra incógnita se obtiene sustituyendo el valor obtenido en las ecuaciones de partida.
- Para sistemas con más de 2 ecuaciones se procede de forma análoga al método 2x2. En el caso particular de sistemas lineales se usará el método de reducción de Gauss.
Nota: Este método se puede usar siempre que los sistemas sean de ecuaciones lineales. En caso contrario, sólo se podrá usar en contadas ocasiones en las que las ecuaciones cumplan ciertos requisitos, como ocurre en el siguiente ejemplo:
Ejemplo: Método de reducción
Resuelve el siguiente sistema:
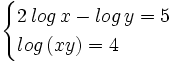
Aplicamos la propiedad del logaritmo de un producto en la segunda ecuación:
Sumando ambas ecuaciones, tenemos:
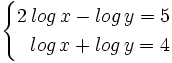
- ___________________________
-
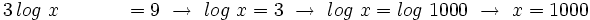
Sustituyendo ese valor de  en la segunda ecuación, tenemos:
en la segunda ecuación, tenemos:
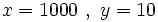
Resuelve por el método de reducción previo cambio de variable:
Resuelve por el método de reducción previo cambio de variable:
Resuelve:
Resuelve:
Resuelve:
Resuelve:
a) 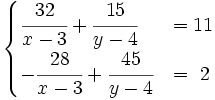
b) 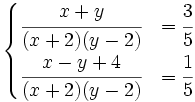
Actividades y problemas
Sistemas con mas de 2 incógnitas:
Tutorial que explica la resolución de sistemas de ecuaciones con más de dos variables, resolviendo varios ejercicios utilizando tanto la sustitución como la reducción.
Resuelve:
Resuelve:
Resuelve:
a) 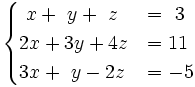
b) 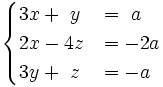
Sistemas 3x2:
Resolución de sistemas lineales 3x2:
1. 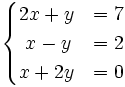 2.
2. 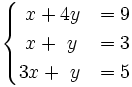 3.
3. 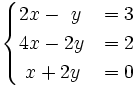
4. 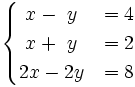 5.
5. 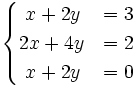 6.
6. 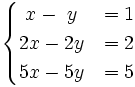
Sistemas cuadráticos:
Tutorial que explica de forma completa la resolución de sistemas de ecuaciones cuadráticos, resolviendo varios ejercicios utilizando tanto la sustitución como la reducción.
Resolución de sistemas de ecuaciones cuadráticos por igualación, reducción y sustitución.
Problemas resueltos por medio de sistemas de ecuaciones cuadráticos.
Sistemas logarítmicos:
Tutorial que trabaja los sistemas de ecuaciones logarítmicas, realizando dos planteamientos posibles para su resolución, agrupando logaritmos o bien por cambio de base.
Resolución de sistemas de ecuaciones logarítmicos.
Sistema de ecuaciones logarítmicas.
Sistema de ecuaciones logarítmicas.
Sistema de ecuaciones logarítmicas.
Sistema de ecuaciones logarítmicas.
Sistemas de ecuaciones logarítmicas.
Sistemas exponenciales:
Resolución de sistemas de ecuaciones exponenciales.
Resolución de un problema de números mediante un sistema lineal 3x3.
Resolución de un problema de números que invierten sus cifras mediante un sistema lineal 3x3.
Resolución de un problema de precios mediante un sistema lineal 3x3.
- Juan y María son hermanos. El tiene tantos hermanos como hermanas, y ella tiene doble número de hermanos que de hermanas. ¿Cuántos hermanos hay de cada sexo?
- Determine las dimensiones de un rectángulo sabiendo que su área aumenta 600 m2 al duplicar los lados, aumentando 340 m2 si la base disminuye 2 m y la altura se triplica.
- Determine un número de dos dígitos sabiendo que es el cuadruplo de la suma de éstos y que al invertir el orden de los dígitos aumenta 36 unidades.
- Determine un número de dos dígitos si la suma de éstos es 11 y al invertir el orden de los dígitos resulta un número que se diferencia 36 unidades del primero.
- Desde un tren que circula a 72 km/h entra en un túnel hasta que sale el último vagón pasan 49 segundos, y pasan 37 segundos desde que el último vagón entra en el túnel hasta que la locomotora aparece en el otro extremo. Determine las respectivas longitudes del tren y el túnel.
Cálculo de la parábola que pasa por tres o cuatro puntos.
Ejercicios resueltos sobre sistemas de ecuaciones exponenciales.
Ejercicios resueltos sobre sistemas de ecuaciones logarítmicas.
|
Actividad: Resolución de sistemas
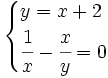
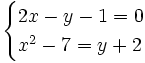
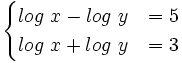 Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios propuestos
|
Ejercicios propuestos: Resolución de sistemas de ecuaciones |