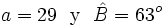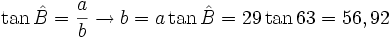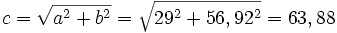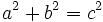Triángulos rectángulos (PACS)

De Wikipedia

Menú:

Enlaces internos	Para repasar	Enlaces externos
Indice CD Alumno 07 Resueltos 07 Descartes Manual Casio	Trigonometría (ppt)	WIRIS Calculadora

Tabla de contenidos

1 Triángulo rectángulo
2 Teorema de Pitágoras
3 Aplicaciones del teorema de Pitágoras
4 Resolución de triangulos rectángulos

[editar]

Triángulo rectángulo

Triángulo rectángulo se denomina al triángulo en el que uno de sus ángulos es recto, es decir, mide 90º (grados sexagesimales) o π/2 radianes.

Se denomina hipotenusa al lado mayor del triángulo, el lado opuesto al ángulo recto.

Se llaman catetos a los dos lados menores, los que conforman el ángulo recto.

[editar]

Teorema de Pitágoras

Teorema de Pitágoras

En un triángulo rectángulo la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos:

$a^2+b^2=c^2\;\!$

donde $a\;\!$ y $b\;\!$ son los catetos y $c\;\!$ la hipotenusa.

Este teorema se debe a Pitágoras de Samos (aprox. 582 a.C.- 507 a.C.)

Demostración:

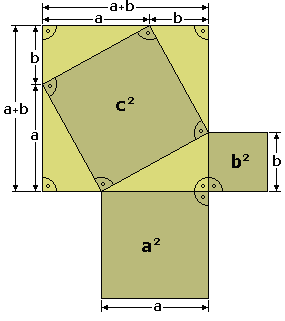
Fíjate en la figura de la derecha y observa como el cuadrado grande, de lado

a + b

, puede descomponerse en un cuadrado de lado

c

y 4 triángulos rectángulos, como el de partida, de catetos

a

b

e hipotenusa

c

La superficie del cuadrado grande de lado $a + b$ es: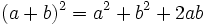

$(a+b)^2=a^2+b^2+2ab\;\!$

La superficie de los cuatro triángulos rectángulos es :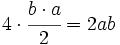

$4 \cdot \cfrac {b \cdot a}{2}=2ab$

Restando el área del cuadrado grande de lado $a + b$ menos las areas de los 4 triángulos rectángulos, se obtiene el área del cuadrado de lado $c$ :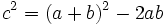

$c^2=(a+b)^2-2ab\;\!$

Desarrollando el cuadrado del binomio: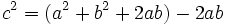

$c^2=(a^2+b^2+2ab)-2ab\;\!$

De donde obtenemos, simplificando: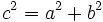

$c^2=a^2+b^2 \;\!$

Teorema de Pitágoras

Teorema de Pitágoras:

Tutorial 1 (7'24") Sinopsis:

Teorema de Pitágoras. Ejemplos y ejercicios.

Tutorial 2 (10'54") Sinopsis:

Teorema de Pitágoras. Ejemplos y ejercicios.

Tutorial 3 (2'17") Sinopsis:

Teorema de Pitágoras. Ejemplos.

Tutorial 4 (2'15") Sinopsis:

Teorema de Pitágoras y recíproco. Ejemplo.

Demostraciones:

Demostración 1 (4´29") Sinopsis:

Demostración del teorema de Pitágoras mediante una construcción geométrica, con ejemplos previos de casos particulares.

Demostración 2 (5'00") Sinopsis:

La misma demostración del teorema de Pitágoras mediante una construcción geométrica, sin ejemplos previos.

Demostración 3

Otra demostración basada en el teorema de la altura y el teorema del cateto.

Consta de tres partes:

1. Teorema de la altura (13´57") Sinopsis:

Demostración del teorema de de la altura.

2. Teorema del cateto (16´16") Sinopsis:

Demostración del teorema del cateto.

3. Teorema de Pitágoras (15´24") Sinopsis:

Demostración del teorema de Pitágoras.

Otros videos:

Pitágoras y su teorema (9'56") Sinopsis:

Pitágoras. El teorema de Pitágoras. Demostraciones.

Pitágoras: mucho más que un teorema (25´) Sinopsis:

Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema. Pero las Matemáticas le deben a Pitágoras y a los pitagóricos mucho más. Ellos son los que pusieron las primeras piedras científicas no solo de la Geometría sino también de la Aritmética, de la Astronomía y de la Música. Pero antes de Pitágoras otras dos culturas habían desarrollado unas matemáticas prácticas muy potentes: los babilonios y los egipcios. Exploraremos sus aportaciones tanto en el terreno de los sistemas de numeración que empleaban, como de sus habilidades astronómicas y geométricas. Del sistema sexagesimal de los babilonios hemos heredado tanto la división de la circunferencia en 360 grados como la forma actual de medir el tiempo en horas, minutos y segundos. Sus tablillas nos reservan unas cuantas sorpresas matemáticas. Quizás la más importante, la tablilla Plimpton, nos desvela el hecho sorprendente de que conocían las ternas pitagóricas mil años antes de que Pitagoras viera la luz.Disfrutaremos de alguna de las demostraciones gráficas más llamativas del famoso teorema, el que cuenta con un mayor número de demostraciones distintas a lo largo de la historia.

Teorema de Pitágoras

Demostraciones gráficas Descripción:

Esta unidad didáctica presenta varias demostraciones del teorema de Pitágoras.

Comprobación geométrica Descripción:

En esta escena podrás comprobar el teorema de Pitágoras mediante el procedimiento gráfico de los cuadrados construidos sobre los lados del triángulo.

[editar]

Aplicaciones del teorema de Pitágoras

Actividades Interactivas: Aplicaciones del teorema de Pitágoras

Actividad 1: Conocidos los catetos: a=4 cm. y b=5 cm., calcular la hipotenusa, c.

Actividad:

Usaremos el teorema de Pitágoras: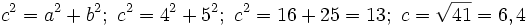

$c^2=a^2+b^2;\ c^2=4^2+5^2;\ c^2=16+25=13;\ c=\sqrt {41}=6,4$

Compruébalo en la escena siguiente:

Click aquí si no se ve bien la escena

Actividad 2: Conocido un cateto a=5 cm. y la hipotenusa c=8 cm., calcular el otro cateto, b.

Actividad:

Usaremos, de nuevo, el teorema de Pitágoras: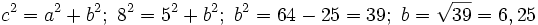

$c^2=a^2+b^2;\ 8^2=5^2+b^2;\ b^2=64-25=39;\ b=\sqrt {39}=6,25$

Compruébalo en la escena siguiente:

Click aquí si no se ve bien la escena

Actividad 3: El tamaño de las pantallas de televisión viene dado por la longitud en pulgadas de la diagonal de la pantalla (una pulgada equivale a 2,54 cm). Si un televisor mide 34,5 cm de base y 30 cm de altura, ¿cuál será su tamaño?

Actividad:

Actividad 4: Halla la altura de un triángulo equilatero de 4 cm. de lado.

Actividad:

Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Si tienes problemas para resolver el ejercicio, utiliza el botón de la parte inferior "pasos" para ir viendo el camino a seguir.

Click aquí si no se ve bien la escena

Actividad 5: Halla la altura de un triángulo isósceles cuyos lados miden c=5 cm. y a=b=4 cm.

Actividad:

Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Para ello tendrás que mover los vértices del triángulo y usar "la regla" (segmento negro) para medir la altura.

Click aquí si no se ve bien la escena

Actividad 6: Calcular el área de un cuadrado inscrito en una circunferencia de 3 cm de radio.

Actividad:

Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Si tienes problemas para resolver el ejercicio, utiliza el botón de la parte inferior "pasos" para ir viendo el camino a seguir.

Click aquí si no se ve bien la escena

[editar]

Resolución de triangulos rectángulos

Cuando decimos resolver un triángulo nos referimos a que encontramos todas sus magnitudes desconocidas, es decir la longitud de sus tres lados y la medida de sus tres ángulos, a partir de las conocidas.

Si un triángulo es rectángulo en realidad ya sabemos una cosa, que tiene un ángulo de 90º, así que nos hará falta menos información para resolverlo. Podemos resolver un tirángulo rectángulo si conocemos:

Dos lados
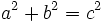
- Podemos calcular el tercer lado con el Teorema de Pitágoras $a^2+b^2=c^2\,\!$
- Cuando sabemos lo que miden los tres lados es fácil encontrar los ángulos a partir de las razones trigonométricas y de la relación entre los ángulos de un triángulo.

Ejemplo

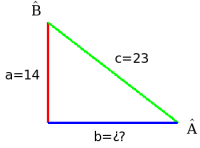
Tenemos este triángulo y sabemos que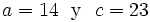 $a= 14 \ \mbox{ y } \ c = 23\,\!$

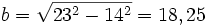
$b=\sqrt{23^2-14^2}=18,25$

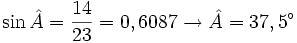
$\sin \hat A = \frac{14}{23}=0,6087 \rightarrow \hat A=37,5^\circ$

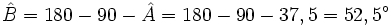
$\hat B = 180 - 90 - \hat A=180-90-37,5 = 52,5^\circ\,\!$

Un ángulo y un lado
- Los lados se calculan mediante la razón trigonométrica del ángulo que tenemos y con la longitud del lado que tenemos
- El ángulo que nos falta se calcula recordando que los ángulos de un triángulo suman entre los tres 180º siempre.

Ejemplo Tenemos este triángulo y conocemos $a=29 \ \mbox{ y } \ \hat B=63^o\,\!$