Porcentajes

De Wikipedia

(Diferencia entre revisiones)

Revisión de 13:46 13 sep 2016

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio	Proporcionalidad		WIRIS Geogebra Calculadora

Tabla de contenidos

1 Definición de porcentaje
2 Representación de los porcentajes
3 Cálculo de un tanto por ciento de una cantidad
4 Obtención del porcentaje correspondiente a una proporción
5 Aumentos y disminuciones porcentuales
6 Calculo de la cantidad inicial conociendo la variación porcentual y la cantidad final
7 Encadenamiento de variaciones porcentuales

Definición de porcentaje

Un porcentaje es una razón entre un número n y 100 y representa las partes que tomamos de un total de 100.
Se representa escribiendo el número seguido del símbolo %, esto es:

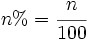$n% = \cfrac{n}{100}$ (se lee " $n\;$ por ciento")

Ejemplos

$\frac{30}{100}=30%; \quad \frac{2}{100}=2%; \quad \frac{120}{100}=120%;\quad \frac{200}{100}=200%;$

Se lee: 30 por ciento; 2 por ciento; 120 por ciento; y 200 por ciento.

Representación de los porcentajes

Podemos representar gráficamente estos porcentajes igual que se hace con las fracciones.

Actividades Interactivas: Representación de porcentajes

Actividad 1. En la siguiente escena se pueden representar porcentajes.

Actividad:

Cambia el valor del porcentaje mediante las flechitas o introduciendo el número y pulsando "Intro".

Click aquí si no se ve bien la escena

Cálculo de un tanto por ciento de una cantidad

Para calcular el tanto por ciento de una cantidad, se expresa el tanto por ciento en forma decimal (dividiéndolo por 100) y se multiplica por la cantidad.

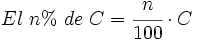
$El \ n% \ de \ C = \cfrac{n}{100} \cdot C$

Ejemplo: Cálculo de un porcentaje

Calcula el 16% de 2000.

Solución:

Método 1: A partir de la definición de pordentaje:

El 16% de 2000 $= \frac{16}{100} \cdot 2000=0,16 \cdot 2000=320$

Método 2: Mediante una regla de tres

  100% ----> 2000
   16% ---->   x

Y despejando $x\;\!$ :

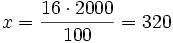
$x=\frac{16 \cdot 2000}{100}= 320$

Actividades Interactivas: Cálculo de porcentajes

Actividad 1. Calcula los siguientes porcentajes en tu cuaderno y luego comprueba los resultados en la escena.

a) 10% de 43; b) 60% de 200; c) 50% de 40; d) 5% de 1000; e) 25% de 400.

Actividad:

Click aquí si no se ve bien la escena

Actividad 2. Calcula mentalmente.

Actividad:

¿Qué resultado es el correcto? Pincha con el ratón el punto rojo y llévalo a la caja del número que te parezca correcto. Para hacer otro ejercicio pulsa el botón inicio

Click aquí si no se ve bien la escena

Ejemplo: Cálculo de la cantidad total a partir del porcentaje

Si en una clase hay 5 alumnos rubios, y representan el 20% de la clase, ¿cuántos alumnos hay en total?

Solución:

Método 1: A partir de la definición de pordentaje:

Si llamamos 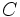$C\;\!$ al total de alumnos de la clase:

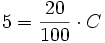
$5=\frac{20}{100} \cdot C$

Y despejando 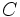$C\;\!$ :

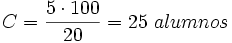
$C=\frac{5 \cdot 100}{20}= 25 \ alumnos$

Método 2: Mediante una regla de tres

   20% ----> 5 alumnos
  100% ----> x alumnos

Y despejando $x\;\!$ :

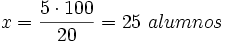
$x=\frac{5 \cdot 100}{20}= 25 \ alumnos$

Obtención del porcentaje correspondiente a una proporción

Procentaje correspondiente a una proporción

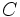Para hallar qué tanto por ciento representa una cantidad, $a\;\!$ , repecto a un total, $C\;\!$ , se efectúa la siguiente operación:

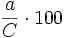
$\frac{a}{C}\cdot 100$

Ejemplo: Porcentaje correspondiente a una proporción

En un grupo del instituto, de 30 alumnos aprueban 21. ¿Qué porcentaje del total representan los aprobados?. ¿Y los suspensos?

Solución:

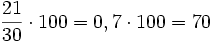
$\frac{21}{30}\cdot 100=0,7 \cdot 100=70$

Por tanto el 70% aprueban y el 30% suspenden.

También podemos hacerlo mediante una regla de tres:

                      %          alumnos
                    ----         -------
 Total:              100   ---->   30 
 Parte (aprobados):   x    ---->   21

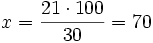
$x=\frac{21 \cdot 100}{30}=70$

Cálculo del porcentaje conocida una parte y el total

Tutorial (5'30") Sinopsis:

Cálculo del porcentaje conocida una parte y el total. Ejemplos.

Ejercicio 1 (2'20") Sinopsis:

¿Qué porcentaje es 425 de 500?

Ejercicio 2 (5'15") Sinopsis:

¿Qué porcentaje de 16 es 4?

Ejercicio 3 (4'38") Sinopsis:

¿Qué porcentaje es 100 de 80?

Problema 1 (1'47") Sinopsis:

Un hotel tiene 300 habitaciones de las que 60 están vacías. ¿Cua´l es el porcentaje de ocupación?

Problema 2 (4'38") Sinopsis:

En México 13 de cada 20 latas son recicladas. ¿Qué porcentaje de latas es reciclado?

Cálculo del porcentaje conocida una parte y el total

Actividad Descripción:

Actividades en las que practicarás el cálculo del porcentaje conocida una parte y el total.

Autoevaluación Descripción:

Actividades de autoevaluación sobre cálculo del porcentaje a partir de la parte y el total.

Aumentos y disminuciones porcentuales

Un aumento porcentual es añadir un porcentaje a una cierta cantidad y una disminución porcentual es quitar un porcentaje a una cierta cantidad.

Proposición

En un aumento/disminución porcentual, se cumple:

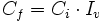$C_f = C_i \cdot I_v$ (CANTIDAD FINAL = CANTIDAD INICIAL · ÍNDICE DE VARIACIÓN)

En aumentos porcentuales del n%, el índice de variación es 1 más el aumento porcentual expresado en forma decimal.

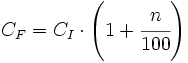$C_F = C_I \cdot \left(1+\cfrac{n}{100} \right)$

En una disminución porcentual del n%, el índice de variación es 1 menos la disminución porcentual puesta en forma decimal.

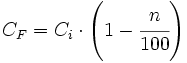$C_F = C_i \cdot \left(1-\cfrac{n}{100}\right)$

Ejemplo: Aumento y disminución porcentual

a) Un litro de leche de 0,95 € aumenta su precio en un 12% ¿Cuánto vale ahora?

b) Unas zapatillas de 120 € se rebajan un 15% ¿Cuál es el valor final?

Solución:

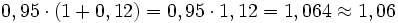a) $0,95 \cdot (1+0,12)=0,95 \cdot 1,12=1,064\approx 1,06$ €

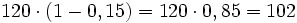b) $120 \cdot (1-0,15)=120 \cdot 0,85=102$ €

Actividades Interactivas: Aumentos y disminuciones porcentuales

Actividad 1. Calcula los siguientes aumentos porcentuales en tu cuaderno y luego comprueba los resultados en la escena.

a) En un instituto hay un 12% más de alumnas que de alumnos. ¿Cuántas alumnas hay sabiendo que hay 150 alumnos?

b) El precio de una bicicleta que costaba 400 € el año pasado, ha subido un 20%.¿Cuál es el precio actual?

c) Actualmente me dan 15 € mensuales de paga, pero he convencido a mis padres para que me suban el 15%. ¿Cuál será mi paga a partir de ahora?

d) ¿Cuánto hay que pagar por un disco de 15 € si hay que sumarle el 16% de IVA?

e) La factura de teléfono de este mes es de 45 € sin IVA. ¿Cuanto será al añadirle el 16% de IVA?

f) ¿Cuánto nos costará dormir una noche en un hotel sabiendo que la habitación vale 70 € sin IVA y el IVA es del 7%?

Actividad:

Click aquí si no se ve bien la escena

Actividad 2. Calcula las siguientes disminuciones porcentuales en tu cuaderno y luego comprueba los resultados en la escena.

a) Un ordenador cuesta este año 850 €. ¿Cuánto costará el año que viene sabiendo que perderá el 40% de su valor?

b) Mis padres me han dado 40 € por mi cumpleaños. ¿Cuánto me quedará al final del día si me gasto el 80% de lo que me han dado?

c) Un trabajador tiene un salario bruto de 980 € al mes, del que le descuentan un 12% en impuestos. ¿Qué salario neto percibe?

d) En una tienda hacen una rebaja del 20% a todos los artículos. ¿Cuanto costará ahora una camisa que antes costaba 35 €? ¿Y un pantalón de 40 €?

e) Tengo 52 € y me quiero comprar un MP3 que costaba antes de las rebajas 60 €. ¿Podré pagarlo si lo rebajan un 15%?

f) Quiero comprarme unas zapatillas de deporte. En una tienda veo dos que me gustan; las primeras tienen un precio de 45 € y una rebaja del 30% y las segundas cuestan 35 € pero no tienen rebaja. ¿Cuáles salen más baratas?

Actividad:

Click aquí si no se ve bien la escena

Calculo de la cantidad inicial conociendo la variación porcentual y la cantidad final

La cantidad inicial se calcula dividiendo la cantidad final por el índice de variación.

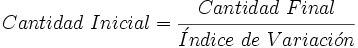$Cantidad \ Inicial = \cfrac{Cantidad \ Final}{\acute{I}ndice \ de \ Variaci \acute{o} n}$

Ejemplo: Cálculo de la cantidad inicial

a) El precio de una moto es de 2800 €. ¿Cuál era el precio de fábrica antes de aplicarle el 16 % de aumento por el IVA?.

b) En las rebajas has comprado unas zapatillas de 90 €, con un descuento del 28 %. ¿Cuánto valía antes de la rebaja?

Solución:

a) Por ser un aumento porcentual, el índice de variación es: 1 + 0,16 = 1,16. Por tanto, el precio inicial de la moto es

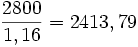$\frac{2800}{1,16}= 2413,79$ €

b) Por ser una disminución porcentual, el índice de variación es: 1 - 0,28 = 0,72. Por tanto, el precio inicial de la moto es

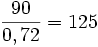$\frac{90}{0,72}= 125$ €

Encadenamiento de variaciones porcentuales

Para encadenar aumentos y disminuciones porcentuales, se multiplican los índices de variación de los sucesivos pasos, siendo el producto el índice de variación del encadenamiento

Ejemplo: Encadenamiento porcentual

El precio de un litro de gasoil era de 102 céntimos de € en el mes de Junio. Subió un 3% en el mes de Agosto y un 4% en el mes de Septiembre.

a) Calcula el precio final tras las dos subidas.

b) ¿Ha subido un 3+4=7%?. ¿Qué porcentaje a subido?

Solución:

a) El precio final es: 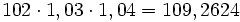$102 \cdot 1,03 \cdot 1,04= 109,2624$ céntimos de €

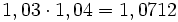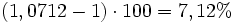b) No, pués el índice de variación total es $1,03 \cdot 1,04 = 1,0712 \;\!$ , es decir un aumento del $(1,0712-1) \cdot 100=7,12%$ .

Problemas: Encadenamiento porcentual

1. El precio de un libro, 12 €, primero sube el 5 %, después sube el 10 % y, finalmente, baja el 15 %.

a) ¿Cuál es su precio final? ¿Es igual que el inicial?

b) ¿Cúal es el índice de variación total, y a qué porcentaje de aumento o de disminución corresponde?

Solución:

a) 11,78 €. No

b) I.V. = 0,98175, entonces una disminución o descuento del 1,825 %

2. Según un artículo de un periódico, a unos trabajadores en el año 2002 se les sube el sueldo un 2%, en el 2003 el 3%, en el 2004 el 4% y los dos siguientes el 1%. ¿Es cierta la afirmación que en los 5 últimos años, a los trabajadores se les ha subido el sueldo un 2 + 3 + 4 + 1 + 1 = 11%?

Solución:

No, pués el índice de variación total = 1,02 . 1,03 . 1,04 . 1,01 . 1,01 = 1,1146, es decir un aumento del 11,46%

Obtenido de "http://maralboran.org/wikipedia/index.php/Porcentajes"

Categorías: Matemáticas | Números

 {{Caja_Amarilla|texto=
 *Un '''aumento porcentual''' es añadir un porcentaje a una cierta cantidad y una '''disminución porcentual''' es quitar un porcentaje a una cierta cantidad.
-<br>
+}}
-*El número por el que hay que multiplicar la cantidad inicial para obtener la cantidad final se llama '''índice de variación'''.
+{{p}}
+{{Teorema_sin_demo|titulo=Proposición|enunciado=:En un aumento/disminución porcentual, se cumple:
 {{p}}
+<center> </CENTER>
+{{P}}
 {{Caja|contenido=
-<center> <math>Cantidad \ Final = Cantidad \ Inicial \cdot \acute{I}ndice  \ de \ Variaci \acute{o} n</math> </CENTER>
+<center> <math>C_f = C_i \cdot I_v</math>{{b4}}{{b4}}(CANTIDAD FINAL = CANTIDAD INICIAL · ÍNDICE DE VARIACIÓN)</CENTER>
 }}
 <br>
 {{p}}
 {{Caja|contenido=
-<center> <math>Cantidad \ Final = Cantidad \ Inicial \cdot \left(1+\cfrac{n}{100} \right)</math> </CENTER>
+<center> <math>C_F = C_I \cdot \left(1+\cfrac{n}{100} \right)</math> </CENTER>
 }}
 <br>
 {{p}}
 {{Caja|contenido=
-<center> <math>Cantidad \ Final = Cantidad \ Inicial \cdot \left(1-\cfrac{n}{100}\right)</math> </CENTER>
+<center> <math>C_F = C_i \cdot \left(1-\cfrac{n}{100}\right)</math> </CENTER>
 }}

Porcentajes

De Wikipedia

Revisión de 13:46 13 sep 2016

Tabla de contenidos

Definición de porcentaje

Representación de los porcentajes

Cálculo de un tanto por ciento de una cantidad

Obtención del porcentaje correspondiente a una proporción

Aumentos y disminuciones porcentuales

Calculo de la cantidad inicial conociendo la variación porcentual y la cantidad final

Encadenamiento de variaciones porcentuales

Vistas

Herramientas personales

Menú

Buscar

Herramientas