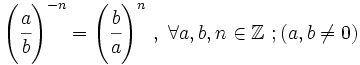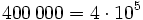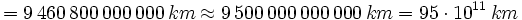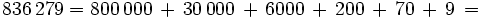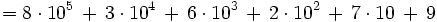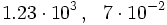Potencias de fracciones (2º ESO)
De Wikipedia
| Revisión de 17:50 1 sep 2017 Coordinador (Discusión | contribuciones) (→Notación científica) ← Ir a diferencia anterior |
Revisión de 17:51 1 sep 2017 Coordinador (Discusión | contribuciones) (→Notación científica) Ir a siguiente diferencia → |
||
| Línea 63: | Línea 63: | ||
| {{Definición: Notacion cientifica}} | {{Definición: Notacion cientifica}} | ||
| {{p}} | {{p}} | ||
| - | {{Actividades descartes notación científica}} | + | {{AI_descartes|titulo1=Ejemplos de números en notación científica |
| + | |descripcion=En la siguiente escena, genera distintos números, pulsando el botón inferior. | ||
| + | |||
| + | Anótalos en tu cuaderno, explicando qué condiciones cumple para que esté en notación científica. | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/1y2_eso/notacion/notacion_cientifica_1.html | ||
| + | width=700 | ||
| + | height=450 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/notacion/notacion_cientifica_1.html | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{AI_descartes|titulo1=Significado del exponente en la notación científica | ||
| + | |descripcion=Consulta la ayuda de la escena y contesta. | ||
| + | |||
| + | Modifica los valores de las cifras y del exponente y observa qué sucede con la coma en los siguientes casos: | ||
| + | |||
| + | *Si el exponente es cero | ||
| + | *Si el exponente es negativo | ||
| + | *Si el exponente es positivo | ||
| + | |||
| + | Anota en tu cuaderno las conclusiones a las que hayas llegado. | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/1y2_eso/notacion/notacion_cientifica_3.html | ||
| + | width=700 | ||
| + | height=350 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/notacion/notacion_cientifica_3.html | ||
| + | }} | ||
| + | |||
| {{Video_enlace_tutomate | {{Video_enlace_tutomate | ||
| |titulo1=Notación científica | |titulo1=Notación científica | ||
Revisión de 17:51 1 sep 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 78)
Potencias de exponente negativo
Se define la potencia de exponente negativo como:

Como consecuencia:
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos.
 . Ejemplos.
. Ejemplos.
Exponentes negativos. Ejemplos.
Razonando sobre el por qué de la definición de los exponentes negativos.
Simplifica:
- a)
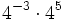
- b)
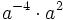
- c)
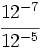
- d)
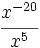
Simplifica:
- a)
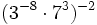
- b)
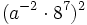
- c)
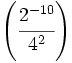
Halla el valor de:
11) 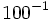 ; 12)
; 12) 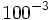 ; 13)
; 13) 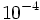 ; 14)
; 14) 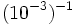
15) 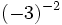 ; 16)
; 16) 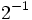 ; 17)
; 17) 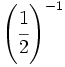 ; 18)
; 18) 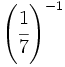 ; 19)
; 19) 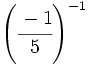
Potencias de exponente negativo.
Actividades sobre potencias de exponente negativo.
Calcula las siguientes potencias y comprueba los resultados en la escena siguiente:
a) 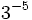 b)
b) 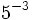 c)
c) 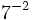 d)
d) 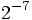
Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba.
Potencias de exponente negativo.
Multiplica y divide potencias (exponentes enteros).
Potencias de productos y cocientes (exponentes enteros)
Potencias de exponentes enteros.
Pulsa el botón "EJERCICIO" y lee atentamente el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien.
Ejercicios de autoevaluación sobre potencias de exponente negativo.
Propiedades de las potencias de números racionales
Las potencias con números racionales cumplen las mismas propiedades que con números enteros.
Ver: Propiedades de las potencias de números enteros
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
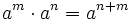
- 2. Cociente de potencias de la misma base:
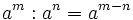
- 3. Potencia de un producto:
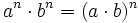
- 4. Potencia de un cociente:
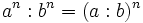
- 5. Potencia de otra potencia:
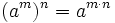
Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa.
Simplifica:
- a)
![\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3](/wikipedia/images/math/f/e/c/fec21991837955f9b9d945d4600cba18.png)
- b)
![\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2}](/wikipedia/images/math/e/5/1/e5178ed20376c4ef7f07ca88d5d43975.png)
Simplifica 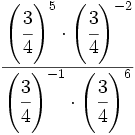
Simplifica: ![\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2](/wikipedia/images/math/6/9/1/6911b07dbbc54e802f87f7498ab77b09.png)
Ejemplos: Potencias de fracciones
Calcula simplificando previamente:
a) 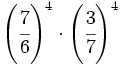 b)
b) 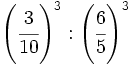 c)
c) 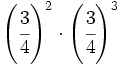
d) 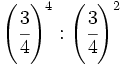 e)
e) 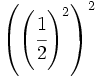 f)
f) 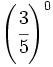
a)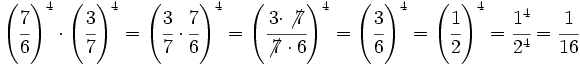
b)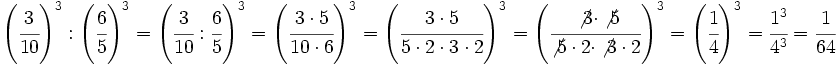
c)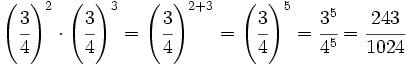
d)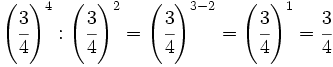
e) 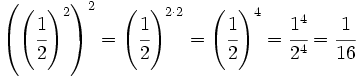
f)
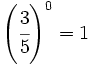
Ejercicios propuestos
|
Ejercicios propuestos: Potencias de fracciones |
Potencias de base 10
Expresión abreviada de números grandes
Potencia de base 10
Una potencia de base 10 es igual a la unidad seguida de tantos ceros como indica el exponente
Esto permite expresar números grandes con muchos ceros como producto de un número por una potencia de 10.
Potencias de 10.
Números naturales expresados como potencias de 10.
Escribe potencias de 10 en forma de número con todas sus cifras.
Expresa cantidades mediante potencias de base 10.
Descomposición polinómica de un número
La descomposición polinómica de un número consiste en expresar dicho número como una suma, en la que cada sumando es cada cifra del número multiplicada por una potencia de 10, cuyo exponente es una unidad menos de la posición que ocupa la cifra que la multiplica.
Actividades para aprender a hallar la descomposición polinómica de un número.
Descomposición polinómica de un número natural. Ejemplos.
Obtén la descomposición polinómica de los siguientes números naturales:
a) 928 b) 5400 c) 208 563 d) 86 324 642
Notación científica
Trabajar con números muy grandes o muy pequeños (muy próximos a cero) resulta engorroso. Por eso debemos aprender a escribir estos números de una forma más abreviada y que resulte más cómoda.
Esta forma de escribirlos es lo que llamaremos notación científica. Veamos en qué consiste:
Un número está en notación científica si aparece expresado de la forma:
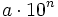
donde  es un número con 1 cifra entera distinta de cero y un número cualquiera de decimales.
es un número con 1 cifra entera distinta de cero y un número cualquiera de decimales.
Ejemplo 1:
- Los siguientes números están en notación científica:
- Estos otros no lo están:
Ejemplo 2:
- La distancia media de la Tierra al Sol es de unos 1500 millones de kilómetros. Si tuviésemos que expresarlo en metros, lo podríamos escribir con todas sus cifras, pero sería más razonable escribirlo en notación científica:
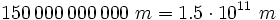
- La masa de un electrón es aproximadamente
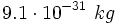 . Si lo escribiésemos con todas sus cifras ...
. Si lo escribiésemos con todas sus cifras ...
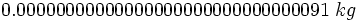
En la siguiente escena, genera distintos números, pulsando el botón inferior.
Anótalos en tu cuaderno, explicando qué condiciones cumple para que esté en notación científica.
Consulta la ayuda de la escena y contesta.
Modifica los valores de las cifras y del exponente y observa qué sucede con la coma en los siguientes casos:
- Si el exponente es cero
- Si el exponente es negativo
- Si el exponente es positivo
Anota en tu cuaderno las conclusiones a las que hayas llegado.
Números en notación científica. Ejemplos.
Actividades para aprender a manejar la notación científica.
- Ejemplos de números muy grandes y muy pequeños.
- Ejercicios resueltos sobre notación científica. Uso de la calculadora.