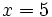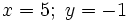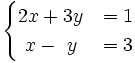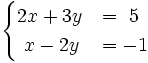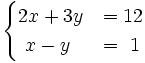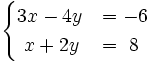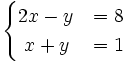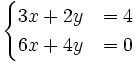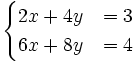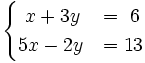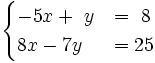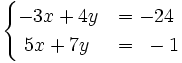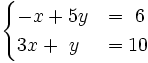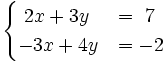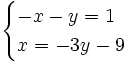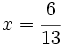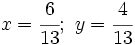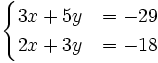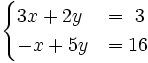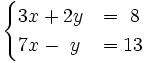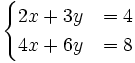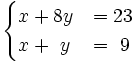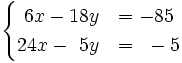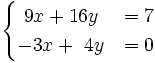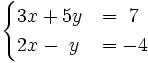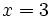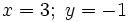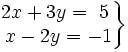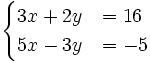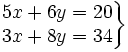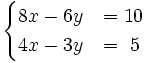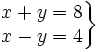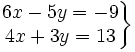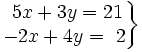Métodos de resolución de sistemas (3ºESO Académicas)
De Wikipedia
| Revisión de 16:48 1 nov 2016 Coordinador (Discusión | contribuciones) (→Resolución de sistemas más complejos) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Resolución de sistemas) |
||
| Línea 39: | Línea 39: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Método de reducción== | ==Método de reducción== | ||
| {{Método de reducción}} | {{Método de reducción}} | ||
| Línea 51: | Línea 52: | ||
| }} | }} | ||
| - | {{p}} | + | ==Actividades== |
| - | ==Resolución de sistemas lineales más complejos== | + | ===Resolución de sistemas=== |
| + | {{Actividades: Resolución de sistemas lineales 2ºESO}} | ||
| + | ===Número de soluciones de un sistema=== | ||
| + | {{Actividades|titulo=Número de soluciones de un sistema|enunciado= | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1a | ||
| + | |descripcion=Número de soluciones de un sistema de ecuaciones: método algebraico. | ||
| + | |url1=http://es.khanacademy.org/math/algebra/systems-of-linear-equations/possible-number-of-solutions-of-systems-of-linear-equations/e/constructing-consistent-and-inconsistent-system | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1b | ||
| + | |descripcion=Número de soluciones de un sistema de ecuaciones: método algebraico. | ||
| + | |url1=http://es.khanacademy.org/math/algebra/systems-of-linear-equations/solving-any-system-of-linear-equations/e/systems_of_equations | ||
| + | }} | ||
| + | }} | ||
| - | ===Ejercicios propuestos=== | + | ==Apéndice== |
| - | {{ejercicio | + | {{Apéndice: sistemas ecuaciones}} |
| - | |titulo=Ejercicios y problemas propuestos: ''Resolución de sistemas lineales más complejos'' | + | ===Manipulación de expresiones=== |
| - | |cuerpo= | + | {{Videotutoriales|titulo=Manipulación de expresiones|enunciado= |
| - | (Pág. 131) | + | {{Video_enlace_khan |
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=1'41" | ||
| + | |sinopsis=Sabiendo que <math>a+b=0\;</math>, ¿cuál de las siguientes expresiones es equivalente a <math>ab\;</math>? | ||
| - | [[Imagen:red_star.png|12px]] 4 | + | :a) <math>b^2\;</math>{{b4}} b) <math>-a^2\;</math>{{b4}} c) <math>\cfrac{a}{b}\;</math>{{b4}} d) <math>2a\;</math>{{b4}} e) <math>0\;</math>{{b4}} |
| + | |url1=https://youtu.be/qQjJasI5B8k | ||
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_khan |
| - | ==Resolución de sistemas no lineales== | + | |titulo1=Ejercicio 2 |
| + | |duracion=3'06" | ||
| + | |sinopsis=Sabiendo que <math>a+b=2a\;</math>, ¿cuál de las siguientes expresiones es equivalente a <math>b-a\;</math>? | ||
| - | ===Ejercicios propuestos=== | + | :a) <math>2b\;</math>{{b4}} b) <math>-b^2\;</math>{{b4}} c) <math>a-b\;</math>{{b4}} d) <math>2a\;</math>{{b4}} e) <math>-2b\;</math>{{b4}} |
| - | {{ejercicio | + | |
| - | |titulo=Ejercicios y problemas propuestos: ''Resolución de sistemas no lineales'' | + | |
| - | |cuerpo= | + | |
| - | (Pág. 132) | + | |
| - | + | ||
| - | [[Imagen:red_star.png|12px]] 1 | + | |
| + | |url1=https://youtu.be/2PFzfWQZ-uM | ||
| }} | }} | ||
| - | |||
| - | {{p}} | ||
| - | |||
| - | ==Resolución de problemas mediante sistemas== | ||
| - | |||
| - | ===Ejercicios propuestos=== | ||
| - | {{ejercicio | ||
| - | |titulo=Ejercicios y problemas propuestos: ''Resolución de sistemas'' | ||
| - | |cuerpo= | ||
| - | (Pág. 133) | ||
| - | |||
| - | [[Imagen:red_star.png|12px]] 1, 2 | ||
| - | |||
| }} | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=manipulación de expresiones | ||
| + | |descripcion=Autoevaluación: Manipula expresiones para obtener otras equivalentes. | ||
| + | |url1=http://es.khanacademy.org/math/algebra/systems-of-linear-equations/manipulating-expressions-with-unknown-variables/e/structure-in-expressions-1}} | ||
| {{p}} | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 128)
Ya conocemos el método gráfico para resolver un sistema de ecuaciones lineales. Ahora vamos a ver tres métodos algebraicos: los métodos de sustitución, igualación y reducción.
Método de sustitución
Procedimiento
Para resolver un sistema por el método de sustitución se siguen los siguientes pasos:
- Se despeja una incógnita en una de las ecuaciones (la que resulte más fácil de despejar).
- Se sustituye la incógnita despejada en (1) en la otra ecuación, obteniendo una ecuación con una sola incógnita.
- Se resuelve la ecuación obtenida en (2), averiguando así una de las incógnitas del sistema.
- El valor obtenido en (3) se sustitute en la expresión de la incógnita despejada en (1), averiguando así el valor de la incógnita que faltaba, y, por tanto, resolviendo el sistema.
Ejemplo: Método de sustitución
Resuelve por el método de sustitución el siguiente sistema:
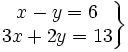
- Despejamos la
 en la primera ecuación:
en la primera ecuación:
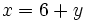 [1]
[1]- Sustituimos esta expresión de la
 en la segunda ecuación:
en la segunda ecuación:
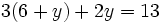
- Resolvemos la ecuación resultante:
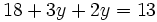
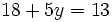
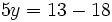
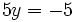
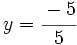
|
|
- Para obtener el valor de
 , sustituimos el valor
, sustituimos el valor 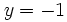 en [1]:
en [1]:
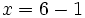
|
|
- Así, la solución del sistema es:
|
|
Método de sustitución. Ejemplo.
Método de sustitución. Ejemplos.
Tutorial en el que se muestra la resolución de sistemas de ecuaciones lineales (grado 1) de dos variables por el método de sustitución.
Videotutorial sobre el método de sustitución para casos sencillos.
Resuelve por el método de sustitución:
Resuelve por el método de sustitución:
Resuelve por el método de sustitución:
Resuelve por el método de sustitución:
Resolución de sistemas lineales 2x2 por el método de sutitución:
Resuelve por el método de sustitución:
Resuelve por el método de sustitución:
Resuelve por el método de sustitución:
Resuelve por el método de sustitución:
Resuelve por el método de sustitución:
Resuelve por el método de sustitución:
Actividades en las que aprenderás el método de sustitución para resolver sistemas de ecuaciones lineales con dos incógnitas.
Actividades en las que aprenderás el método de sustitución para resolver sistemas de ecuaciones lineales con dos incógnitas.
Resolver sistemas de ecuaciones por el método de sustitución.
Ejercicios de autoevaluación sobre el método de sustitución para la resolución de sistemas de ecuaciones lineales.
Ejercicios resueltos sobre el método de sustitución para la resolución de sistemas de ecuaciones lineales.
Ejercicios propuestos
|
Ejercicios propuestos: Método de sustitución |
Método de igualación
Procedimiento
Para resolver un sistema por el método de igualación se siguen los siguientes pasos:
- Se despeja la misma incógnita en las dos ecuaciones del sistema.
- Se igualan las expresiones obtenidas en (1), con lo que se obtiene una ecuación con una sola incógnita.
- Se resuelve la ecuación obtenida en (2), averiguando así una de las incógnitas del sistema.
- El valor obtenido en (3) se sustitute en una de las dos expresiones de la incógnita despejada en (1), averiguando así el valor de la incógnita que faltaba, y, por tanto, resolviendo el sistema.
Ejemplo: Método de igualación
Resuelve por el método de igualación el siguiente sistema:
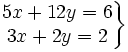
- Despejamos la
 en cada una de las dos ecuaciones:
en cada una de las dos ecuaciones:
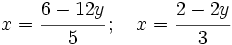 [1]
[1]- Igualamos estas dos expresiones:
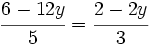
- Resolvemos la ecuación:
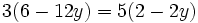
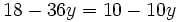
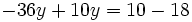
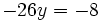
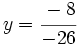
|
|
- Sustituimos el valor
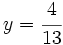 en cualquiera de las expresiones de [1], por ejemplo en
en cualquiera de las expresiones de [1], por ejemplo en 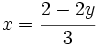 :
:
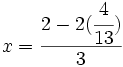
|
|
- Así, la solución del sistema es:
|
|
Método de igualación. Ejemplo.
Resolución de sistemas por igualación. Ejemplos.
Resuelve por el método de igualación:
Resuelve por el método de igualación:
Resuelve por el método de igualación:
Resuelve por el método de igualación:
Resolución de sistemas lineales 2x2 por el método de igualación:
Resuelve por el método de igualación:
Resuelve por el método de igualación:
Resuelve por el método de igualación:
Resuelve por el método de igualación:
Resuelve por el método de igualación:
Actividades en las que aprenderás el método de igualación para resolver sistemas de ecuaciones lineales con dos incógnitas.
Ejercicios de autoevaluación sobre el método de igualación para la resolución de sistemas de ecuaciones lineales.
Ejercicios resueltos sobre el método de igualación para la resolución de sistemas de ecuaciones lineales.
Ejercicios propuestos
|
Ejercicios propuestos: Método de igualación |
Método de reducción
Procedimiento
Para resolver un sistema por el método de reducción o eliminación se siguen los siguientes pasos:
- Se obtiene un sistema equivalente al de partida, multiplicando las dos ecuaciones por números apropiados, de manera que una de las incógnitas quede con coeficentes opuestos en ambas ecuaciones.
- Se suman las ecuaciones del nuevo sistema, desapareciendo así la incógnita con coeficientes opuestos.
- Se resuelve la ecuación obtenida en (2), averiguando así una de las incógnitas del sistema.
- El valor obtenido en (3) se sustitute en una de las dos ecuaciones del sistema de partida, averiguando así el valor de la incógnita que faltaba, y, por tanto, resolviendo el sistema.
Ejemplo: Método de reducción
Resuelve por el método de reducción el siguiente sistema:
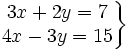
- Multiplicamos la primera ecuación por 4 y la segunda por (-3)
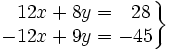
- Sumamos miembro a miembro las dos ecuaciones:
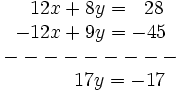
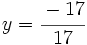
|
|
- Sustituimos el valor
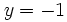 en cualquiera de las dos ecuaciones del sistema de partida, por ejemplo en la primera:
en cualquiera de las dos ecuaciones del sistema de partida, por ejemplo en la primera: 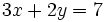
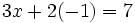
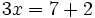
|
|
- Así, la solución del sistema es:
|
|
Método de reducción. Ejemplo.
Resolución de sistemas por reducción. Ejemplos.
Tutorial en el que se muestra la resolución de sistemas de ecuaciones lineales (grado 1) de dos variables por el método de reducción.
Resuelve por el método de reducción:
Resuelve por el método de reducción:
Resuelve por el método de reducción:
Resuelve por el método de reducción:
Resolución de sistemas lineales 2x2 por el método de reducción:
Resolución de sistemas lineales 2x2 por el método de reducción:
Resuelve gráficamente:
Resuelve gráficamente:
Resuelve gráficamente:
Resuelve gráficamente:
Resuelve gráficamente:
Resuelve por el método de reducción:
Resuelve por el método de reducción:
- a)
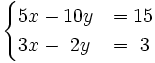
- b)
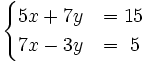
Actividades en las que aprenderás el método de reducción para resolver sistemas de ecuaciones lineales con dos incógnitas.
Actividades en las que aprenderás el método de reducción para resolver sistemas de ecuaciones lineales con dos incógnitas.
Ejercicios de autoevaluación sobre el método de reducción para la resolución de sistemas de ecuaciones lineales.
Ejercicios de autoevaluación sobre el método de reducción para la resolución de sistemas de ecuaciones lineales.
Ejercicios de autoevaluación sobre el método de reducción para la resolución de sistemas de ecuaciones lineales.
Ejercicios resueltos sobre el método de reducción para la resolución de sistemas de ecuaciones lineales.
Ejercicios propuestos
|
Ejercicios propuestos: Método de reducción |
Actividades
Resolución de sistemas
Ejercicios resueltos sobre resolución de sistemas utilizando los tres métodos.
Resuelve:
a) 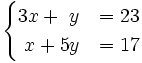
b) 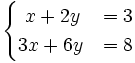
Número de soluciones de un sistema
Número de soluciones de un sistema de ecuaciones: método algebraico.
Número de soluciones de un sistema de ecuaciones: método algebraico.
Apéndice
Tutorial que explica la resolución de sistemas de ecuaciones con más de dos variables, resolviendo varios ejercicios utilizando tanto la sustitución como la reducción.
Tutorial que explica de forma completa la resolución de sistemas de ecuaciones cuadráticos, resolviendo varios ejercicios utilizando tanto la sustitución como la reducción.
Manipulación de expresiones
Sabiendo que  , ¿cuál de las siguientes expresiones es equivalente a
, ¿cuál de las siguientes expresiones es equivalente a 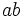 ?
?
- a)
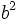 b)
b) 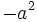 c)
c) 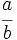 d)
d) 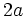 e)
e) 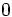
Sabiendo que 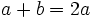 , ¿cuál de las siguientes expresiones es equivalente a
, ¿cuál de las siguientes expresiones es equivalente a 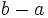 ?
?
- a)
 b)
b)  c)
c) 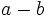 d)
d) 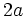 e)
e) 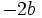
Autoevaluación: Manipula expresiones para obtener otras equivalentes.