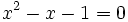Números Reales (4ºESO Académicas)
De Wikipedia
| Revisión de 11:10 9 jul 2008 Juanmf (Discusión | contribuciones) (→Conjuntos numéricos) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Representación gráfica de números reales en la recta real) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Conjuntos numéricos== | + | __TOC__ |
| - | {{Caja_Amarilla|texto=El conjunto formado por los números racionales y los irracionales se llama conjunto de los ''números reales'' y se designa por <math>\mathbb{R}</math>.}} | + | {{Dios creó los números naturales}} |
| {{p}} | {{p}} | ||
| - | En el siguiente esquema puedes ver todos los conjuntos númericos con los que hemos trabajado hasta ahora: | + | ==Números reales== |
| + | {{Def numeros reales}} | ||
| + | {{p}} | ||
| + | {{Videos y actividades: números reales}} | ||
| + | {{p}} | ||
| + | ===Operaciones con números reales. Propiedades=== | ||
| + | {{Operaciones con números reales. Propiedades}} | ||
| + | {{p}} | ||
| + | ===La recta real=== | ||
| + | {{La recta real}} | ||
| + | {{p}} | ||
| + | ===Representación gráfica de números reales en la recta real=== | ||
| + | {{Representación gráfica de números reales en la recta real}} | ||
| + | |||
| + | ===Ejercicios propuestos=== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Números reales'' | ||
| + | |cuerpo= | ||
| + | |||
| + | (Pág. 15) | ||
| - | <center> | + | [[Imagen:red_star.png|12px]] 1 |
| - | <math> | + | |
| - | \mbox{Reales } (\mathbb{R}) | + | |
| - | \begin{cases} | + | |
| - | \mbox{Racionales }(\mathbb{Q}) | + | |
| - | \begin{cases} | + | |
| - | \mbox{Enteros } (\mathbb{Z}) | + | |
| - | \begin{cases} | + | |
| - | \mbox{Naturales } (\mathbb{N})\rightarrow 0,1,\frac{16} {2},\sqrt{9}\\ | + | |
| - | \mbox{Enteros negativos}\rightarrow -1,\frac{-16} {2},\sqrt{9} | + | |
| - | \end{cases}\\ | + | |
| - | \mbox{Fraccionarios}\rightarrow 5,23;\frac{5} {2};0,\widehat{54};-\frac{5} {2} | + | |
| - | \end{cases}\\ | + | |
| - | \mbox{Irracionales } (\mathbb{I})\rightarrow \pi=3.141592654..., e=2.718281..., \varphi = \frac{1 + \sqrt{5}}{2} = 1.618033988... ,\sqrt{2}=1.414213... | + | |
| - | \end{cases} | + | |
| - | </math> | + | |
| - | </center> | + | |
| + | [[Imagen:yellow_star.png|12px]] 2 | ||
| + | }} | ||
| [[Categoría: Matemáticas|Números]][[Categoría: Números|Reales]] | [[Categoría: Matemáticas|Números]][[Categoría: Números|Reales]] | ||
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
| "Dios creó los números naturales, lo demás es obra de los hombres." |
Números reales
El conjunto de los números reales es el formado por la unión de los números racionales y de los números irracionales y se designa por  En el siguiente esquema puedes ver todos los conjuntos númericos con los que hemos trabajado hasta ahora: 
| 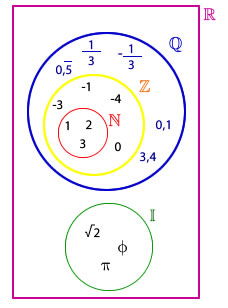 El conjunto de los números realesde portaleduativo.net |
Números naturales, enteros, racionales, irracionales y reales. Ejemplos.
Todo lo que necesitas saber sobre los distintos tipos de números reales (naturales, enteros, racionales e irraciones). Tutorial que explica de forma matemática y no tan matemática los conjuntos numéricos y como han ido surgiendo en demanda a las necesidades a la hora de poder resolver problemas aritméticos.
Introducción a números racionales e irracionales.
Clasifica en racionales e irracionales los siguientes números:
Clasificación de números reales.
Escena en la que se resume los distintos tipos de conjuntos nunéricos vistos hasta ahora.
Clasifica los siguientes números en racionales e irracionales.
Indica a que conjuntos de números pertenece un número dado.
Pulsa el botón "Ejercicio" para generar un ejercicio. Te dan un número y debes decir todos los conjuntos a los que pertenece. Luego pulsa el botón "Solución" para ver si lo has hecho bien.
Copia los ejercicios que hagas en tu cuaderno.
Ejercicios de autoevaluación sobre números reales.
Operaciones con números reales. Propiedades
Operaciones con números reales. Propiedades.
Ejercicios de autoevaluación sobre las propiedades de las operaciones con números reales.
La recta real
La recta real es una representación geométrica del conjunto de los números reales.
Para su construcción:
- Se elige un punto de referencia arbitrario sobre la recta al que se denomina origen y al que se le asocia el número 0.
- Se selecciona una unidad U de longitud para medir distancias que es la que separa los números 0 y 1.
- Se elige también un sentido a lo largo de la recta a la que se llama positivo y se considera como negativo al sentido opuesto.
- A cada número real p se le asocia un punto de la recta que está a una distancia de p unidades del origen en la dirección positiva o negativa, dependiendo de si el número p es positivo o negativo, respectivamente.
El conjunto de los números reales es la unión del conjunto de los números racionales (tienen un número finito de decimales o son periódicos) y del conjunto de los números irracionales (tienen infinitos decimales y no son periódicos). La "visualización" del conjunto de los números reales es la llamada "recta real": a cada número real le corresponde un único "punto" de la "recta real" y viceversa: cada "punto" de la recta real corresponde a un único número real. Por eso, consideraremos sinónimas las palabras "número" y "punto".
Los números reales en la recta real.
Mueve el punto rojo y observa que todo punto de la recta representa un número real. Utiliza el zoom para ampliar la vista, si lo deseas.
Luego introduce distintos número y observa su representación en la recta real:
- Introduce las fracciones
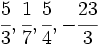 (teclea a/b para introducir la fracción
(teclea a/b para introducir la fracción  )
)
- Introduce la raíz cuadrada de 2, 5, 7, 11 (teclea sqrt(n) para introducir la raíz cuadrada de n)
Densidad de los números racionales e irracionales
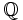 es denso en
es denso en  : Entre cada dos números reales existe un racional, y por tanto hay infnitos.
: Entre cada dos números reales existe un racional, y por tanto hay infnitos.
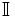 es denso en
es denso en  : Entre cada dos números reales existe un irracional, y por tanto hay infnitos.
: Entre cada dos números reales existe un irracional, y por tanto hay infnitos.
Completitud de los números reales
Gracias al axioma del supremo o axioma de completitud, el conjunto de los números reales cubre o completa la recta sin dejar "huecos". Existe una correspondencia biunívoca entre los puntos de la recta y los números reales de manera que a cada punto de la recta le hace corresponder un único número real y viceversa.
Este video te servirá en el tema de límites para manipular mejor expresiones con límites infinitos.
Recta real ampliada: conjunto que resulta al añadir los símbolos +∞ y -∞ al conjunto de los reales. Que quede muy claro: +∞ y -∞ no son números, y para todo real "x" es -∞ < x < +∞.
Representación gráfica de números reales en la recta real
En los siguientes ejemplos puedes ver distintos procedimientos de representación, dependiendo de cómo sea el número real que queramos representar:
- Entero o decimal exacto: Vamos intentar representar un número al azar, el 3,24 por ejemplo, buscamos el 3,2 primero, "ampliamos" buscamos el 3,24 y marcamos.
- Decimal periódico: Hacemos con la regla una recta oblicua a la primera y que mida un múltiplo del denominador dividimos esta nueva recta en tantas partes como indique el denominador (si el denominador es 6 dividimos en siete partes), unimos sus extremos y trazamos las paralelas.
- Radical cuadrático: Podemos representar un radical cuadrático teniendo en cuenta el teorema de Pitágoras. En el ejemplo, se muestra como se ha representado
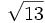
- Resto de irracionales: En este caso se toma su expresión aproximada decimal y se afina tanto como se quiera empleando el método mostrado en decimales exactos.
A continuación vamos a ver algunas actividades interactivas y videos sobre la representación de algunos números irracionales en la recta real.
Observa en la escena la representación de  .
.
- Para ello debes ir presionando sucesivamente el control pasos.
- Toma nota en tu cuaderno de los pasos de la representación e intenta realizarla con regla y compás.
- Si presionas sobre el control decimales podrás variar el número de cifras decimales.
Observa en la escena la representación de otras raices cuadradas.
- Pulsando sobre el control pasos puedes observar cómo se representa la raíz cuadrada de cualquier número entero.
- Representa en tu cuaderno la raíz de 3 y la raíz de 5.
- Pulsando el control decimales puedes obtener el número de ellos que desees.
- Utiliza el botón Limpiar si quieres ver con más claridad la representación de algún número.
En esta escena podrás ver como se representan gráficamente los números del tipo 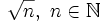 .
.
En esta escena podrás ver como se representan gráficamente algunas raíces cuadradas.
Ejercicios de autoevaluación sobre representación gráfica de números irracionales.
En la escena puedes ver la construcción del número de oro basada en una construcción gráfica que se encuentra en un libro de Euclides (siglo III a.C.).
- Para ello debes ir presionando sucesivamente el control pasos.
- Toma nota en tu cuaderno de los pasos de la representación e intenta realizarla con regla y compás.
- Si presionas sobre el control decimales podrás variar el número de cifras decimales.
Construcción con regla y compás de la sección áurea de un segmento y del rectángulo áureo.
|
Actividad: Números reales a) Representa los números b) ¿Es -5 un número entero? c) ¿Es 5/3 un número racional? d) ¿Es pi un numero irracional? e) ¿Cual es el valor del número de oro? f) Resuelve la ecuación g) ¿Recuerdas cómo se escribe 75 en números romanos? Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) number line 0, 1, 5, golden number, pi b) is -5 an integer? c) is 5/3 a rational number? d) Is pi an irrational number? e) golden number f) solve x^2-x-1=0, o bien, solve x^2-x-1=0 over the reals g) 75 in roman numerals |
Ejercicios propuestos
|
Ejercicios propuestos: Números reales |
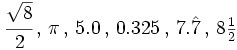

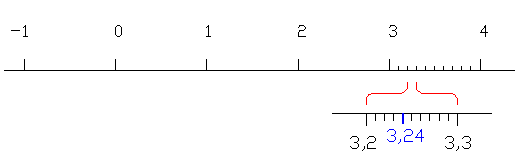
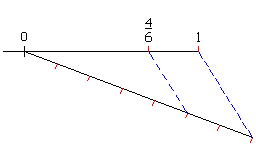
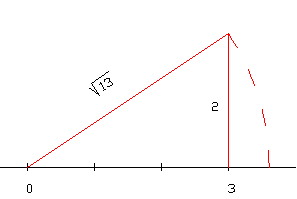
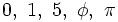 en la recta numérica.
en la recta numérica.