Relaciones de proporcionalidad entre magnitudes (1º ESO)
De Wikipedia
| Revisión de 17:11 4 sep 2017 Coordinador (Discusión | contribuciones) (→Relación de proporcionalidad inversa) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Magnitudes proporcionales) |
||
| Línea 9: | Línea 9: | ||
| ==Introducción== | ==Introducción== | ||
| {{Introducción proporciones}} | {{Introducción proporciones}} | ||
| - | |||
| {{p}} | {{p}} | ||
| ==Razón y proporción== | ==Razón y proporción== | ||
| - | {{Razón y proporción 1ºESO}}{{p}} | + | {{Razón y proporción 1ºESO}} |
| + | {{p}} | ||
| (Pág. 152) | (Pág. 152) | ||
| + | |||
| + | ==Relaciones de proporcionalidad== | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=3'22" | ||
| + | |sinopsis=Concepto de magnitud. Magnitudes directamente e inversamente proporcionales. | ||
| + | |||
| + | |url1=https://youtu.be/cuZUYbdt8aM?list=PLwCiNw1sXMSA5afCSBZn9Y9X9F732nicE | ||
| + | }} | ||
| ==Relación de proporcionalidad directa== | ==Relación de proporcionalidad directa== | ||
| Línea 21: | Línea 30: | ||
| ==Relación de proporcionalidad inversa== | ==Relación de proporcionalidad inversa== | ||
| - | {{Caja_Amarilla|texto=Dos magnitudes son '''inversamente proporcionales''' cuando al multiplicar (resp. dividir) una de ellas por un número, la otra queda dividida (resp. multiplicada) por el mismo número. | + | {{Relación de proporcionalidad inversa 1ºESO}} |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | + | |
| - | El '''número de obreros''' que trabajan en una construcción y el '''tiempo que tardan''' en finalizarla son magnitudes '''inversamente proporcionales''', ya que si el número de obreros es el doble (o el triple,...), el tiempo que tardan será la mitad (o la tercera parte, ...). | + | |
| - | {{p}} | + | |
| - | <center> | + | |
| - | <table border="1" width="60%"> | + | |
| - | <tr> | + | |
| - | <td width="28%"><p align="center"><strong><font size="2">Número de obreros</font></strong></p></td> | + | |
| - | <td width="14%"><p align="center"><font size="2">2</font></p></td> | + | |
| - | <td width="14%"><p align="center"><font size="2">4</font></p></td> | + | |
| - | <td width="14%"><p align="center"><font size="2">10</font></p></td> | + | |
| - | <td width="14%"><p align="center"><font size="2">20</font></p></td> | + | |
| - | </tr> | + | |
| - | <tr> | + | |
| - | <td width="28%"><p align="center"><strong><font size="2">Tiempo que tardan (horas)</font></strong></p></td> | + | |
| - | <td width="14%"><p align="center"><font size="2">20</font></p></td> | + | |
| - | <td width="14%"><p align="center"><font size="2">10</font></p></td> | + | |
| - | <td width="14%"><p align="center"><font size="2">4</font></p></td> | + | |
| - | <td width="14%"><p align="center"><font size="2">2</font></p></td> | + | |
| - | </tr> | + | |
| - | </table> | + | ==Actividades== |
| - | </center> | + | {{AI_enlace|titulo1=Actividad: ''Proporciones y magnitudes directamente proporcionales'' |
| + | |descripcion= | ||
| + | |url1=http://quizlet.com/198271868/match | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{AI_vitutor | ||
| - | |titulo1=Autoevaluación: ''Magnitudes inversamente proporcionales'' | ||
| - | |descripcion=Ejercicios de autoevaluación sobre magnitudes inversamente proporcionales. | ||
| - | |url1=http://www.vitutor.com/di/p/a_8e.html | ||
| - | }} | ||
| - | {{p}} | ||
| - | ===Constante de proporcionalidad inversa=== | ||
| - | {{Teorema_sin_demo|titulo=Propiedad|enunciado=Al multiplicar dos magnitudes inversamente proporcinales siempre se obtiene el mismo valor. A dicho valor se le denomina '''constante de proporcionalidad inversa'''.}} | ||
| - | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| - | En el ejemplo anterior, en el que relacionabamos el número de obreros y el tiempo que tardan en finalizar una obra | ||
| - | {{p}} | ||
| - | <center> | ||
| - | <table border="1" width="60%"> | ||
| - | <tr> | ||
| - | <td width="28%"><p align="center"><strong><font size="2">Número de obreros</font></strong></p></td> | ||
| - | <td width="14%"><p align="center"><font size="2">2</font></p></td> | ||
| - | <td width="14%"><p align="center"><font size="2">4</font></p></td> | ||
| - | <td width="14%"><p align="center"><font size="2">10</font></p></td> | ||
| - | <td width="14%"><p align="center"><font size="2">20</font></p></td> | ||
| - | </tr> | ||
| - | <tr> | ||
| - | <td width="28%"><p align="center"><strong><font size="2">Tiempo que tardan (horas)</font></strong></p></td> | ||
| - | <td width="14%"><p align="center"><font size="2">20</font></p></td> | ||
| - | <td width="14%"><p align="center"><font size="2">10</font></p></td> | ||
| - | <td width="14%"><p align="center"><font size="2">4</font></p></td> | ||
| - | <td width="14%"><p align="center"><font size="2">2</font></p></td> | ||
| - | </tr> | ||
| - | |||
| - | </table> | ||
| - | </center> | ||
| - | |||
| - | se observa que: | ||
| - | |||
| - | <center><math>2 \cdot 20 = 4 \cdot 10 = 10 \cdot 4 = 20 \cdot 2 = 40</math> </center> | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{AI_cidead | ||
| - | |titulo1=Relación de proporcionalidad inversa | ||
| - | |||
| - | |descripcion=Actividades para que aprendas y practiques el cálculo de la constante de proporcionalidad inversa y sus uso para resolver problemas de proporcionalidad inversa. | ||
| - | |||
| - | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena4/2quincena4_contenidos_3a.htm | ||
| - | }} | ||
| - | |||
| - | ==Ejercicios== | ||
| {{AI_anaya|titulo1=Actividades: ''Identificando el tipo de relación de proporcionalidad'' | {{AI_anaya|titulo1=Actividades: ''Identificando el tipo de relación de proporcionalidad'' | ||
| |descripcion= | |descripcion= | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/09/02.htm | + | url=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/09/02.htm |
| width=800 | width=800 | ||
| height=650 | height=650 | ||
| Línea 104: | Línea 47: | ||
| </iframe></center> | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/09/02.htm | + | |url1=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/09/02.htm |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 119: | Línea 62: | ||
| }} | }} | ||
| - | [[Categoría: Ejercicios de Matemáticas|Números]] | + | [[Categoría: Matemáticas]][[Categoría: Aritmética]] |
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Introducción
Un toque divertido para empezar el tema:
La aventura más Manga de Troncho y Poncho (a lo japonés). Es como si los Pokemon explicasen las magnitudes directa e inversamente proporcionales.
Puedes encontrar ejercicios sobre este vídeo y material similar en: http://www.angelitoons.com/
Razón y proporción
Tutorial en el que se explica y trabaja la proporción numérica, la razón de proporción, y cuando cuatro números guardan proporción.
- 00:00 a 02:40: Introducción (ejemplos).
- 02:40 a 03:15: Definición de razón (de proporción) entre dos cantidades (números).
- 03:15 a 05:24: Ejemplos 1-2-3 de razón (de proporción) entre dos números.
- 05:24 a 08:15: Ejemplo 4 de aplicación de razón.
- 08:15 a 09:40: Definición de cuándo cuatro números guardan proporción. Producto de medios y producto de extremos.
- 09:40 a 12:20: Ejemplos 5-6-7 de razón de proporción entre dos números. - 12:20 a Fin: Ejemplo 8 de aplicación de razón.
Estamos acostumbrados a dar información sobre situaciones de la vida cotidiana usando números. Hay ocasiones en las que un solo número no es suficiente y debemos compararlo con otra cantidad para poder comprender mejor la situación. Cuando comparamos dos cantidades formamos una razón.
Razón es el cociente entre dos números,  y
y  . Se escribe
. Se escribe 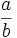 y se lee "
y se lee " es a
es a  ".
".
- Toda fracción puede ser considerada como una razón, pero no toda razón es una fracción, ya que una fracción es el cociente de dos números enteros, pero en una razón los números no tienen que ser necesariamente enteros.
- Cuando digamos "razón de a y b" nos referiremos habitualmente al cociente a/b, pero según el contexto, podremos considerar a/b o b/a, indistintamente.
- Podemos expresar una razón como número decimal o, cuando sea posible, como fracción.
- Una razón no tiene unidades y sirve para comparar, ya que indica el nº de veces que una cantidad es mayor que otra.
Concepto de razón.
Explicación de qué es una razón y presentación de algunos ejemplos en los que se aplican las razones
Aprenderemos qué es una razón (ratio), es decir, el cociente de dos magnitudes y qué significa.
Una razón es una comparación de dos cantidades. Aprende a encontrar la relación entre dos cosas, por ejemplo, entre el número de manzanas y el de naranjas.
Aviso: A veces, se tiende a confundir el término "razón" con el de "proporción". Por ejemplo, en este video se habla de "proporción de manzanas en relación con naranjas". En realidad debe decirse "razón entre manzanas y naranjas". El significado del término "proporción" lo veremos posteriormente.
En este video utilizamos razones parte:todo para encontrar la relación entre el número frutas de un tipo (la parte) con el número total de ellas (el todo).
Aviso: A veces, se tiende a confundir el término "razón" con el de "proporción". Por ejemplo, en este video se habla de "proporción del número de manzanas en relación con el número de frutas". En realidad debe decirse "razón entre el número de manzanas y el de frutas". El significado del término "proporción" lo veremos posteriormente.
Una tasa es una razón. En este video presentamos las tasas por medio de ejemplos como 60 km por hora o 200 calorías por porción.
- En una primera escena te presentamos varios ejemplos de razón entre dos números para entender qué nos indica.
- En otra actividad te proponemos que halles la razón en tres casos concretos.
Razón ente dos números.
Razón ente dos números.
Una proporción es una igualdad entre dos razones: 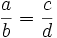 . En tal caso, se dice que ambas razones son equivalentes.
. En tal caso, se dice que ambas razones son equivalentes.
Para entender la definición anterior fíjate en el siguiente ejemplo.
Quieres hacer una copia ampliada de una foto carné. Quieres que esa foto sea exactamente igual que la que ya tienes, pero más grande, es decir, que se respete la forma, pero no el tamaño. Lógicamente si duplicas el largo de la foto, estás obligado a duplicar el alto, ya que de lo contrario no se respetaría la forma original (saldría estirada o achatada). Matemáticamente, para que la nueva foto sea proporcional, la razón entre el largo de la ampliación y el largo de la original tiene que ser igual a la razón entre el ancho de la ampliación y el ancho de la original. Y eso es lo que dice la definición, una proporción es una igualdad de razones.
Con proporción
| Sin proporción
|
Explicación de qué es una proporción y presentación de algunos ejemplos en los que se aplican las proporciones.
Conceptos de proporción.
- En una primera escena te presentamos varios ejemplos de proporciones.
- En otra actividad te proponemos que compruebes si dos razones dadas forman o no una proporción.
Ejercicios de autoevaluación sobre proporciones.
Cálculo del cuarto proporcional
Se llama cuarto proporcional al término que desconocemos en una proporción.
Dado que si dos fracciones son equivalentes "el producto de medios es igual al de extremos", podemos calcular cualquier término de una proporción conociendo los otros tres.
Procedimiento
Para calcular el cuarto proporcional igualaremos el producto de extremos al producto de medios y despejaremos la incógnita:
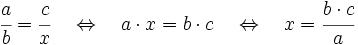
Halla el valor de "n" en la proporción 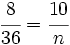 .
.
Actividades para aprender y practicar el cálculo del cuarto proporcional.
Actividades para aprender y practicar el cálculo del cuarto proporcional.
Actividades para aprender y practicar el cálculo del cuarto proporcional.
Resolver proporciones.
Ejercicios de autoevaluación sobre cuartos proporcionales.
Actividades y videotutoriales
Completa la tabla sabiendo que la razones entre los elementos de las columnas son equivalentes.
En una clase de idiomas, la razón de niñas a niños es 5 a 8. Si hay 65 estudiantes, ¿cuántas niñas hay?
Majo tarda 3 horas en repartir 189 periódicos en su ruta. ¿Cuál es la razón por hora en la que entrega periódicos?
El servicio de limpieza Miranda cobra $2800 por limpiar 8 oficinas. ¿Cuál es el precio que cobra la compañía por limpiar una oficina?
Problema de comparación de tasas a partir de un tabla.
Distintos ejemplos de razón y proporcionalidad.
Aprende a completar tablas de razones equivalentes.
Problemas verbales de razones equivalentes (proporciones).
Comprender razones equivalentes (proporciones).
Razones equivalentes a partir de diagramas de barras.
Razones equivalentes y unidades de medida.
Razones parte:todo a partir de diagramas de barras.
Ejercicios:
- Calcula la razón de cada par de números y expresa el resultado como un número decimal.
- De las siguientes parejas de números, escoge aquellas que tengan razón 3/5.
- Calcula el término desconocido para cada proporción.
(Pág. 152)
Relaciones de proporcionalidad
Concepto de magnitud. Magnitudes directamente e inversamente proporcionales.
Relación de proporcionalidad directa
Cálculo del valor de varios a partir del valor de uno
Dos magnitudes son directamente proporcionales cuando al multiplicar (resp. dividir) una de ellas por un número distinto de cero, la otra queda multiplicada (resp. dividida) por el mismo número.
Es muy común pensar que dos magnitudes son directamente proporcionales si al aumentar (resp. disminuir) una de ellas, aumenta (resp. disminuye) la otra. No es exactamente así. No es suficiente con que aumente (resp. disminuya) la otra magnitud, tiene que hacerlo de una forma muy concreta: Si multiplicamos (resp. dividimos) una, se multiplica (resp. divide) la otra, por el mismo número.
La capacidad de un depósito de agua y el tiempo que tarda en llenarse son magnitudes directamente proporcionales, ya que si el depósito tiene el doble (o el triple,...) de capacidad, el tiempo que tarda en llenarse es el doble (o el triple,...).
Capacidad (litros) |
100 |
200 |
300 |
400 |
500 |
Tiempo (min) |
5 |
10 |
15 |
20 |
25 |
Magnitudes directamente proporcionales. Ejemplo.
Magnitudes directamente proporcionales. Ejemplos.
Relaciones directamente proporcionales. Ejemplo.
Aviso: En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales".
Hoy Nate tiene 100 plátanos. Él va a comer 2 plátanos de ellos cada día.
- a) ¿El número de plátanos que Nate deja sin comer es directamente proporcional al número de días transcurridos?
- b) ¿Y el número de plátanos que come cada día?
Aviso: En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales".
Un cine cobra $10.50 por boleto y $5 por bolsa de palomitas. Tú nunca compras las palomitas porque te parece que son muy caras. ¿El precio total de lo que pagas es directamente proporcional al número de boletos que compras?
Aviso: En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales".
Actividades para aprender que son magnitudes directamente proporcionales.
Actividades sobre magnitudes directamente proporcionales.
Completa las tablas de manera que las magnitudes sean directamente proporcionales.
Actividades sobre magnitudes directamente proporcionales.
Actividad sobre magnitudes directamente proporcionales.
Ejercicios de autoevaluación sobre magnitudes directamente proporcionales.
Ejercicios de autoevaluación sobre magnitudes directamente proporcionales.
Constante de proporcionalidad directa
Al dividir dos magnitudes directamente proporcionales siempre se obtiene el mismo valor. A dicho valor se le llama constante o razón de proporcionalidad.
En el ejemplo anterior, en el que relacionabamos la capacidad de un depósito con el tiempo que tardaba en llenarse
Capacidad (litros) |
100 |
200 |
300 |
400 |
500 |
Tiempo (min) |
5 |
10 |
15 |
20 |
25 |
se observa que:
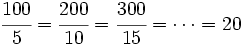
La constante de proporcinalidad es 20.
Razón de proporcionalidad directa. Ejemplo.
Actividades para aprender a calcular la constante de proporcionalidad directa.
Actividades para aprender a calcular la constante de proporcionalidad directa.
Halla la constante de proporcionalidad.
(Pág. 153)
Relación de proporcionalidad inversa
Dos magnitudes son inversamente proporcionales cuando al multiplicar (resp. dividir) una de ellas por un número distinto de cero, la otra queda dividida (resp. multiplicada) por el mismo número.
Es muy común pensar que dos magnitudes son inversamente proporcionales si al aumentar (resp. disminuir) una de ellas, disminuye (resp. aumenta) la otra. No es exactamente así. No es suficiente con que disminuya (resp. aumente) la otra magnitud, tiene que hacerlo de una forma muy concreta: Si multiplicamos (resp. dividimos) una, se divide (resp. multiplica) la otra, por el mismo número.
El número de obreros que trabajan en una construcción y el tiempo que tardan en finalizarla son magnitudes inversamente proporcionales, ya que si el número de obreros es el doble (o el triple,...), el tiempo que tardan será la mitad (o la tercera parte, ...).
Número de obreros |
2 |
4 |
10 |
20 |
Tiempo que tardan (horas) |
20 |
10 |
4 |
2 |
Magnitudes inversamente proporcionales. Razón de proporcionaledad inversa.
Ejercicios de autoevaluación sobre magnitudes inversamente proporcionales.
Ejercicios de autoevaluación sobre magnitudes inversamente proporcionales.
Constante de proporcionalidad inversa
Propiedad
Al multiplicar dos magnitudes inversamente proporcinales siempre se obtiene el mismo valor. A dicho valor se le denomina constante de proporcionalidad inversa.
En el ejemplo anterior, en el que relacionabamos el número de obreros y el tiempo que tardan en finalizar una obra
Número de obreros |
2 |
4 |
10 |
20 |
Tiempo que tardan (horas) |
20 |
10 |
4 |
2 |
se observa que:
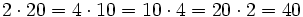
Actividades para que aprendas y practiques el cálculo de la constante de proporcionalidad inversa y sus uso para resolver problemas de proporcionalidad inversa.
Actividades
Ejercicios propuestos
|
Ejercicios propuestos: Relaciones de proporcionalidad entre magnitudes |



