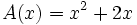Plantilla:Estudio y representación gráfica de funciones (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:02 30 mar 2020 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:17 30 mar 2020 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 10: | Línea 10: | ||
| #'''[[Ramas infinitas. Asíntotas (1ºBach) | Asíntotas y ramas infinitas]]'''. | #'''[[Ramas infinitas. Asíntotas (1ºBach) | Asíntotas y ramas infinitas]]'''. | ||
| #'''[[Funciones: Definición (1ºBach)#Simetrías de una función |Simetrías]]''': ver si f(x) es par ( f(x) = f(-x) ) o impar ( f(x) = - f(-x) ). | #'''[[Funciones: Definición (1ºBach)#Simetrías de una función |Simetrías]]''': ver si f(x) es par ( f(x) = f(-x) ) o impar ( f(x) = - f(-x) ). | ||
| + | }} | ||
| + | {{wolfram desplegable|titulo=Expresión analítica de una función|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Expresión analítica de una función'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | |||
| + | Representa las siguientes funciones: | ||
| + | |||
| + | # <math>A(x)=x^2+2x\;</math> | ||
| + | # <math>B(x)=\cfrac{x+4}{x^2-1}\;</math> | ||
| + | |||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | # {{consulta|texto=Plot A(x)=x^3+2x^2+4x-1}} | ||
| + | |||
| + | # {{consulta|texto=Plot B(x)=(x+4)/(x^2-1)}} | ||
| + | |||
| + | |||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
| }} | }} | ||
Revisión de 17:17 30 mar 2020
En este tema vamos a hacer uso de toda la artillería de la que disponemos y que hemos ido viendo a lo largo de los temas anteriores.
Procedimiento
En el estudio y representación gráfica de una función, f(x), tendremos que considerar los siguientes apartados:
- Dominio de definición.
- Puntos de corte con los ejes de coordenadas, especialmente con el eje de abscisas (eje X). Los puntos de corte con el eje X se obtienen resolviendo la ecuación f(x)=0. El punto de corte con el eje Y se obtiene calculando f(0).
- Signo: para su estudio usaremos los puntos de corte y los puntos de discontinuidad. Éstos determinaran una serie de intervalos en el dominio de la función en los que ésta tiene signo constante. Tomando un punto cualquiera de cada zona y sustituyéndolo en f(x), tendremos el signo de la función en cada zona.
- Intervalos de crecimiento y decrecimiento. Máximos y mínimos: hallando los puntos singulares ( f '(x)=0 ) para estudiar el signo de f '(x).
- Asíntotas y ramas infinitas.
- Simetrías: ver si f(x) es par ( f(x) = f(-x) ) o impar ( f(x) = - f(-x) ).
Actividad: Expresión analítica de una función Representa las siguientes funciones: Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
