Estudio y representación de funciones (1ºBach)
De Wikipedia
| Revisión de 19:10 12 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Apéndice) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | __TOC__ | ||
| + | ==Estudio y representación gráfica de funciones== | ||
| + | {{Estudio y representación gráfica de funciones (1ºBach)}} | ||
| + | |||
| + | {{p}} | ||
| + | |||
| + | ==Estudio y representación gráfica de funciones polinómicas== | ||
| {{Representación de funciones polinómicas (1ºBach)}} | {{Representación de funciones polinómicas (1ºBach)}} | ||
| + | {{p}} | ||
| + | |||
| + | ===Ejercicios propuestos=== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Estudio y representación de funciones polinómicas'' | ||
| + | |cuerpo= | ||
| + | (Pág. 316) | ||
| + | |||
| + | [[Imagen:red_star.png|12px]] 1b,c | ||
| + | |||
| + | [[Imagen:yellow_star.png|12px]] 1a | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | ==Estudio y representación gráfica de funciones racionales== | ||
| + | {{Estudio y representación gráfica de funciones racionales (1ºBach)}} | ||
| + | |||
| + | {{p}} | ||
| + | |||
| + | ===Ejercicios propuestos=== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Estudio y representación de funciones racionales'' | ||
| + | |cuerpo= | ||
| + | (Pág. 318) | ||
| + | |||
| + | [[Imagen:red_star.png|12px]] 2b,c,e | ||
| + | |||
| + | [[Imagen:yellow_star.png|12px]] 2a,d,f | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | ==Apéndice== | ||
| + | {{Videotutoriales | ||
| + | |titulo=Estudio y representación gráfica de otras funciones | ||
| + | |enunciado= | ||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Ejercicio 1a (exponencial) | ||
| + | |duracion=15'43" | ||
| + | |sinopsis=Representación gráfica de <math>f(x)=e^{1-x}\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=JulYyOS0hH4 | ||
| + | }} | ||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Ejercicio 1b (logarítmica) | ||
| + | |duracion=23'54" | ||
| + | |sinopsis=Representación gráfica de <math>f(x)=ln \, \cfrac{1}{1-x}\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=EvDCxmwr82A | ||
| + | }} | ||
| + | {{Video_enlace_matesandres | ||
| + | |titulo1=Ejercicio 2a (irracional) | ||
| + | |duracion=30'56" | ||
| + | |sinopsis=Representación gráfica de <math>f(x)=\sqrt{x^2-10x}\;</math> sin estudio de concavidad. | ||
| + | |||
| + | |url1=https://youtu.be/akSVuDk_lhw?list=PLNQqRPuLTic-0-vxURmFwCNC2wlp1a_Sb | ||
| + | }} | ||
| + | {{Video_enlace_matesandres | ||
| + | |titulo1=Ejercicio 2b (logarítmica) | ||
| + | |duracion=22'48" | ||
| + | |sinopsis=Representación gráfica de <math>f(x)=ln \,(4-2x)\;</math> con estudio de concavidad. | ||
| + | |||
| + | |url1=https://youtu.be/a7mRvMyayVM?list=PLNQqRPuLTic-0-vxURmFwCNC2wlp1a_Sb | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Teoremas|enunciado= | ||
| + | |||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Teorema de Bolzano | ||
| + | |duracion=4'47" | ||
| + | |sinopsis= | ||
| + | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/03-continuidad-de-funciones-2/09-teorema-de-bolzano-2#.WGOhfEZ9U6c | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=La propiedad "D" de Darboux | ||
| + | |duracion=7'08" | ||
| + | |sinopsis=Video tutorial de matematicasbachiller.com | ||
| + | |url1=http://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/03-continuidad-de-funciones/10-la-propiedad-bdb-de-darboux#.WGOgyEZ9U6c | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Teorema de Weierstrass | ||
| + | |duracion=23'26" | ||
| + | |sinopsis= | ||
| + | |url1=http://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/03-continuidad-de-funciones/11-teorema-de-weierstrass#.WGOhCUZ9U6c | ||
| + | }} | ||
| + | }} | ||
| + | {{Wolfram: Representacion grafica de funciones}} | ||
| + | {{p}} | ||
| + | |||
| [[Categoría: Matemáticas]][[Categoría: Funciones]] | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Estudio y representación gráfica de funciones
En este tema vamos a hacer uso de toda la artillería de la que disponemos y que hemos ido viendo a lo largo de los temas anteriores.
Procedimiento
En el estudio y representación gráfica de una función, f(x), tendremos que considerar los siguientes apartados:
- Dominio de definición.
- Puntos de corte con los ejes de coordenadas, especialmente con el eje de abscisas (eje X). Los puntos de corte con el eje X se obtienen resolviendo la ecuación f(x)=0. El punto de corte con el eje Y se obtiene calculando f(0).
- Signo: para su estudio usaremos los puntos de corte y los puntos de discontinuidad. Éstos determinaran una serie de intervalos en el dominio de la función en los que ésta tiene signo constante. Tomando un punto cualquiera de cada zona y sustituyéndolo en f(x), tendremos el signo de la función en cada zona.
- Intervalos de crecimiento y decrecimiento. Máximos y mínimos: hallando los puntos singulares ( f '(x)=0 ) para estudiar el signo de f '(x).
- Concavidad* de f(x): a partir de los puntos singulares de f '(x) y estudiando el signo de f "(x). Es como estudiar el crecimiento de f '(x).
- Asíntotas y ramas infinitas.
- Simetrías: ver si f(x) es par ( f(x) = f(-x) ) o impar ( f(x) = - f(-x) ).
(*) El estudio de concavidad se verá en 2º de bachillerato, aunque se verá como se hace en algún vídeo.
Estudio completo de una función y representación gráfica. Pasos a seguir.
Estudio y representación gráfica de funciones polinómicas
Procedimiento
En el estudio y representación gráfica de una función polinómica, f(x),tendremos que determinar los siguientes apartados:
- Dominio:
 .
.
- Puntos de corte: Los puntos de corte con el eje X se obtienen resolviendo la ecuación f(x)=0, para lo que tendremos que resolver una ecuación polinómica usando las técnicas vistas en temas anteriores. El punto de corte con el eje Y se obtiene calculando f(0).
- Signo de f(x): para el estudio del signo usaremos sólo los puntos de corte ya que una función polinómica no tiene discontinuidades.
- Puntos singulares de f(x) que se obtienen resolviendo la ecuación f '(x)=0. Por tanto, tendremos que resolver otra ecuación polinómica.
- Intervalos de crecimiento y decrecimiento de f(x): a partir de los puntos singulares de f(x) y estudiando el signo de f '(x). Así podremos determinar los máximos y mínimos relativos de f(x).
- Concavidad* de f(x): a partir de los puntos singulares de f '(x) y estudiando el signo de f "(x). Es como estudiar el crecimiento de f '(x).
- Asíntotas y ramas infinitas: Las funciones polinómicas no tienen ningún tipo de asíntotas. Tan sólo habrá que estudiar el límite cuando x tiende a +/- infinito.
- Simetrías: ver si f(x) es par o impar.
(*) El estudio de concavidad se verá en 2º de bachillerato, aunque se verá como se hace en algún vídeo.
Estudio y representación gráfica de la función polinómica 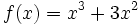
- Dominio
- Puntos de corte con los ejes.
- Crecimiento y puntos extremos.
- Ramas infinitas.
- Representación gráfica.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones polinómicas.
Todo lo que necesitas saber para resolver inecuaciones polinómicas de cualquier grado. Tutorial que explica de forma completa la resolución de estas inecuaciones, empezando por comprender el estudio del signo de un polinomio y resolviendo varios ejericios donde se aplica.
- 00:00 a 01:30: Introducción.
- 1:30 a 10:10: Estudio del Signo de un Polinomio dada su gráfica.
- 10:10 a 17:45: Ejemplo de introducción al algoritmo.
- 17:45a 19:30: Algoritmo de resolución de inecuaciones polinómicas.
- 19:30 a 38:35: Aplicación del algoritmo. Ejemplos resueltos.
Los ceros de un polinomio son los puntos de corte de la función polinómica con el eje X.
En este ejemplo calcularemos los ceros del polinomio 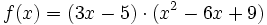
Estudio del crecimiento, puntos extremos y concavidad* de 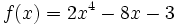
(*) Para ampliar
Estudio y representación gráfica de la función polinómica 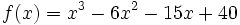 . Incluye estudio de la concavidad (para ampliar).
. Incluye estudio de la concavidad (para ampliar).
Estudio del crecimiento, puntos extremos y concavidad* de la función polinómica f(x) = (x − 1)2. Representación gráfica.
(*) Para ampliar.
Estudio del crecimiento, puntos extremos y concavidad* de la función polinómica f(x) = x4 + 8x3 − 2. Representación gráfica.
(*) Para ampliar.
Estudio del crecimiento, puntos extremos y concavidad* de la función polinómica 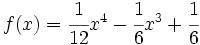 . Representación gráfica.
. Representación gráfica.
(*) Para ampliar.
Estudio del crecimiento, puntos extremos y concavidad* de la función polinómica f(x) = x3 − 6x2 + 9x. Representación gráfica.
(*) Para ampliar.
Estudio del crecimiento, puntos extremos y concavidad* de la función polinómica f(x) = x4 − 2x3. Representación gráfica.
(*) Para ampliar.
Ejercicios resueltos: Estudio y representación gráfica de funciones polinómicas
Estudia y representa:
- a)
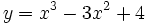 .
.
- b)
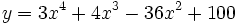 .
.
- c)
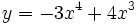 .
.
Utiliza la siguiente escena para comprobar los resultados.
En la siguiente escena puedes ver la representación gráfica de distintas funciones.
Ejercicios propuestos
|
Ejercicios propuestos: Estudio y representación de funciones polinómicas |
Estudio y representación gráfica de funciones racionales
Procedimiento
En el estudio y representación gráfica de una función racional, 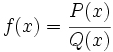 ,tendremos que determinar los siguientes apartados:
,tendremos que determinar los siguientes apartados:
- Dominio:
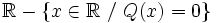 .
.
- Puntos de corte: Los puntos de corte con el eje X se obtienen resolviendo la ecuación f(x)=0, para lo que tendremos que resolver la ecuación polinómica P(x)=0 usando las técnicas vistas en temas anteriores. El punto de corte con el eje Y se obtiene calculando f(0).
- Signo de f(x): para el estudio del signo usaremos los puntos de corte y los puntos de discontinuidad, que son los puntos donde se anula el denominador, es decir, donde Q(x)=0.
- Puntos singulares de f(x) que se obtienen resolviendo la ecuación f '(x)=0. Por tanto, tendremos que resolver otra ecuación polinómica.
- Intervalos de crecimiento y decrecimiento de f(x): a partir de los puntos singulares y estudiando el signo de f '(x). Así podremos determinar los máximos y mínimos relativos de f(x).
- Concavidad* de f(x): a partir de los puntos singulares de f '(x) y estudiando el signo de f "(x). Es como estudiar el crecimiento de f '(x).
- Asíntotas y ramas infinitas:
- A.V.: Son "candidatos" a asíntota vertical los puntos donde Q(x)=0. Habrá que estudiar el límite de f(x) cuando x tiende a esos puntos candidatos. Aquellos para los que ese límite sea + o - infinito serán puntos con A.V.
- A.H.: Cuando el grado de Q(x) sea mayor o igual que el grado de P(x) tendremos asíntota horizontal.
- A.O.: Cuando el grado de P(x) sea igual al grado de Q(x) más uno, tendremos asíntota oblicua.
- Cuando no haya A.H. ni A.O. tendremos ramas infinitas.
- Simetrías: ver si f(x) es par o impar.
(*) El estudio de concavidad se verá en 2º de bachillerato, aunque se verá como se hace en algún vídeo.
Ejercicios resueltos: Estudio y representación gráfica de funciones racionales
Estudia y representa:
- a)
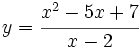 .
.
- b)
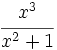 .
.
- c)
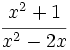 .
.
Utiliza la siguiente escena para comprobar los resultados.
En la siguiente escena puedes ver la representación gráfica de distintas funciones.
Estudio y representación gráfica de la función racional 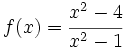
- Dominio
- Puntos de corte con los ejes.
- Crecimiento y puntos extremos.
- Ramas infinitas.
- Representación gráfica.
Estudio y representación gráfica de la función racional 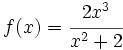
- Dominio
- Puntos de corte con los ejes.
- Crecimiento y puntos extremos.
- Ramas infinitas.
- Representación gráfica.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con quebrados algebraicos.
Representación gráfica de 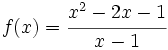
Representación gráfica de 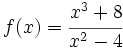
Estudio de las simetrías de:
a) 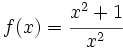
b) 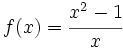
Representación gráfica de 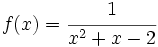 sin estudio de concavidad.
sin estudio de concavidad.
Representación gráfica de 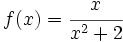 con estudio de concavidad.
con estudio de concavidad.
Representación gráfica de 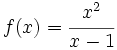 con estudio de concavidad.
con estudio de concavidad.
Ejercicios propuestos
|
Ejercicios propuestos: Estudio y representación de funciones racionales |
Apéndice
Representación gráfica de 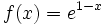
Representación gráfica de 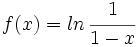
Representación gráfica de 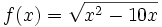 sin estudio de concavidad.
sin estudio de concavidad.
Representación gráfica de 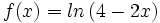 con estudio de concavidad.
con estudio de concavidad.
Video tutorial de matematicasbachiller.com