Teorema de Pitágoras. Aplicaciones
De Wikipedia
| Revisión de 12:25 10 dic 2007 Coordinador (Discusión | contribuciones) (→Teorema de Pitágoras) ← Ir a diferencia anterior |
Revisión de 12:28 10 dic 2007 Coordinador (Discusión | contribuciones) (→Teorema de Pitágoras) Ir a siguiente diferencia → |
||
| Línea 51: | Línea 51: | ||
| </iframe></center> | </iframe></center> | ||
| <center>[http://maralboran.org/web_ma/videos/pitagoras/pitagoras.htm '''Shift-Click''' aquí si no se ve bien la escena]</center> | <center>[http://maralboran.org/web_ma/videos/pitagoras/pitagoras.htm '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| - | <center>[http://c0/helvia/aula/archivos/repositorio/html/98/index.html '''Shift-Click''' aquí para enlace desde servidor TIC]</center> | + | <center>[http://c0/helvia/aula/archivos/repositorio/html/98/index.htm '''Shift-Click''' aquí para enlace desde servidor TIC]</center> |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 12:28 10 dic 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Teorema de Pitágoras
Teorema de Pitágoras
| En un triángulo rectángulo la hipotenusa al cuadrado es igual al cuadrado de la suma de los catetos
| 
|
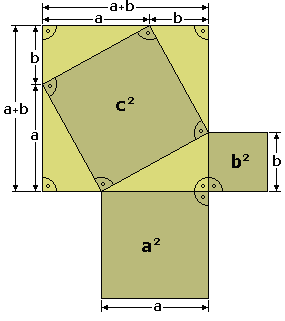
| Fíjate en la figuar de la derecha y observa como el cuadrado grande, de lado a + b, puede descomponerse en un cuadrado de lado c y 4 triángulos rectángulos, como el de partida, de catetos a y b e hipotenusa c.
La superficie del cuadrado grande de lado a + b es: 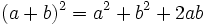 La superficie de los cuatro triángulos rectángulos es : 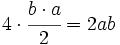 Restando el área del cuadrado grande de lado a + b menos las areas de los 4 triángulos rectángulos, se obtiene el área del cuadrado de lado c: 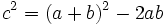 Desarrollando el cuadrado del binomio: 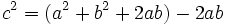 De donde obtenemos, simplificando: 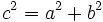 |
Otras demostraciones gráficas
Video: Pitágoras: mucho más que un teorema (25´)
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema. Perolas Matemáticas le deben a Pitágoras y a los pitagóricos mucho más. Ellos son los que pusieron las primeras piedras científicas no solo de la Geometría sino también de la Aritmética, de la Astronomía y de la Música. Pero antes de Pitágoras otras dos culturas habían desarrollado unas matemáticas prácticas muy potentes: los babilonios y los egipcios. Exploraremos sus aportaciones tanto en el terreno de los sistemas de numeración que empleaban, como de sus habilidades astronómicas y geométricas. Del sistema sexagesimal de los babilonios hemos heredado tanto la división de la circunferencia en 360 grados como la forma actual de medir el tiempo en horas, minutos y segundos. Sus tablillas nos reservan unas cuantas sorpresas matemáticas. Quizás la más importante, la tablilla Plimpton, nos desvela el hecho sorprendente de que conocían las ternas pitagóricas mil años antes de que Pitagoras viera la luz.Disfrutaremos de alguna de las demostraciones gráficas más llamativas del famoso teorema, el que cuenta con un mayor número de demostraciones distintas a lo largo de la historia.
Ternas pitagóricas
Se llaman ternas pitagóricas a las ternas de números naturales que verifican el teorema de Pitágoras, por ejemplo 3,4,5. También son ternas pitagóricas sus múltiplos: 6,8,10; 9,12,15 ...
|
Actividades Interactivas: Ternas pitagóricas
1. Comprueba las siguientes ternas pitagóricas.
Actividad: Comprueba que los números 10, 8 y 6 (el doble de 5, 4 y 3) también verifican la relación anterior. Cualquier múltiplo 5*k, 4*k y 3*k de esos tres números (donde k es un número positivo, cualquiera) también la verifican. En el cuadro siguiente varía los valores del parámetro k y comprueba que el triángulo cuyos lados tienen esas medidas siempre es rectángulo y que efectivamente se verifica la relación anterior. Observa que k puede tomar valores decimales. |
Aplicaciones del teorema de Pitágoras
|
Actividades Interactivas: Aplicaciones del teorema de Pitágoras
1. Conocidos los catetos: a=4 cm. y b=5 cm., calcular la hipotenusa, c.
Actividad: Usaremos el teorema de Pitágoras: 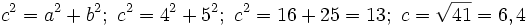 Compruébalo en la escena siguiente:
2. Conocido un cateto a=5 cm. y la hipotenusa c=8 cm., calcular el otro cateto, b.
Actividad: Usaremos, de nuevo, el teorema de Pitágoras: 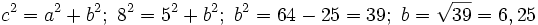 Compruébalo en la escena siguiente:
3. Halla la altura de un triángulo equilatero de 4 cm. de lado.
Actividad: Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Para ello tendrás que mover los vértices del triángulo y usar "la regla" (segmento negro) para medir la altura.
4. Halla la altura de un triángulo isósceles cuyos lados miden c=5 cm. y a=b=4 cm.
Actividad: Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Para ello tendrás que mover los vértices del triángulo y usar "la regla" (segmento negro) para medir la altura. |
Clasificar un triángulo atendiendo a sus ángulos, conocidos sus lados
En un triángulo cualquiera, si llamamos a al lado mayor, y a los otros dos b y c, se cumple que:
- Si a2 > b2 + c2, el triángulo es obtusángulo
- Si a2 = b2 + c2, el triángulo es rectángulo
- Si a2 < b2 + c2, el triángulo es acutángulo
|
Actividad Interactiva: Clasificar un triángulo conocidos sus lados
1. Clasifica los siguientes triángulos:
Actividad: Clasifica los siguientes triángulos, atendiendo a sus ángulos: a) Triángulo de lados 4, 5 y 2. Primero, en tu cuaderno, haz los cálculos necesarios para contestar a las preguntas. A continuación, en la siguiente escena, mueve los puntos para cambiar el valor de los lados y comprueba los resultados que has obtenido. |
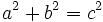
 y
y  son los catetos y
son los catetos y  la hipotenusa.
la hipotenusa.