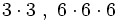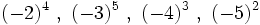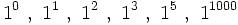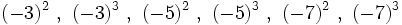Números enteros: Potencias y raíces (1º ESO)
De Wikipedia
| Revisión de 11:59 23 nov 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:09 23 nov 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 5: | Línea 5: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Potencias de enteros== | + | ==Potencias de números enteros== |
| {{Potencias enteros}} | {{Potencias enteros}} | ||
| - | + | {{p}} | |
| + | ==Raíces de números enteros== | ||
| + | Sabemos que {{sube|porcentaje=+20%|contenido=<math>3^2 = 9\;\!</math>}}. Esta igualdad la podemos expresar de forma similar como {{sube|porcentaje=+20%|contenido=<math>\sqrt{9}=3</math>}} y se lee ''3 es igual a la raíz cuadrada de 9''. | ||
| + | En general:{{p}} | ||
| + | {{Caja_Amarilla|texto= | ||
| + | *Se define la '''raíz cuadrada''' de un número {{sube|porcentaje=+15%|contenido=<math>a\;\!</math>}} como otro número {{sube|porcentaje=+15%|contenido=<math>b\;\!</math>}} tal que {{sube|porcentaje=+20%|contenido=<math>b^2 =a\;\!</math>}}, que escribimos simbólicamente: <math>b=\sqrt{a}</math>. | ||
| + | }} | ||
| + | {{p}} | ||
| + | Dependiendo del signo del entero, su raíz puede existir o no. Tenemos los siguientes dos casos: | ||
| + | {{p}} | ||
| + | {{Caja_Amarilla|texto= | ||
| + | *La raíz cuadrada de un número entero '''positivo''' tiene dos soluciones iguales pero opuestas en signo, que no siempre son números enteros. | ||
| + | *La raíz cuadrada de un número entero '''negativo''' no existe. | ||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Números|Enteros]] | [[Categoría: Matemáticas]][[Categoría: Números|Enteros]] | ||
Revisión de 12:09 23 nov 2009
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Potencias de números enteros
Los siguientes videotutoriales condensan lo que vamos a ver en este apartado sobre potencias de números enteros:
Cálculo de potencias cuya base es un número entero. Ejemplos.
Ejemplos de potencias de números enteros.
Tutorial en el que se explica a través de varios ejemplos la potencia con números enteros y las operaciones combinadas con multiplicación, división y potencia de números enteros.
- 00:00 a 05:55: Potencia de número enteros, definición.
- 05:55 a 09:15: Ejercicios simples de Potencias.
- 09:15 a 13:07: Ejercicios de Combinadas de Multiplicación, División y Potencias.
Potencias de números enteros.
Potencias de base entera y exponente natural. Producto de potencias. División de potencias. Potencias de una potencia. Potencia de un producto. Signo de una potencia.
Definición de potencia
La definición de potencia de exponente entero es la misma que la de números naturales.
Ver: Potencias de números naturales
Una potencia es un modo abreviado de escribir un producto de un número por sí mismo:
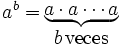 (Se lee: "
(Se lee: " elevado a
elevado a  ")
")- El número
 se llama base. Es el número que se multiplica por sí mismo.
se llama base. Es el número que se multiplica por sí mismo.
- El número
 se llama exponente. Es el número que indica las veces que la base aparece como factor.
se llama exponente. Es el número que indica las veces que la base aparece como factor.
- Por convenio, se establece que:
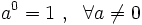 .
.
- Cuando el exponente de una potencia es el número 1 no se pone exponente, basta con poner el número de la base.
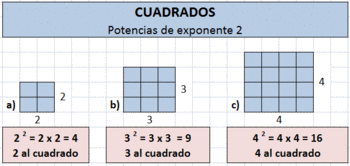
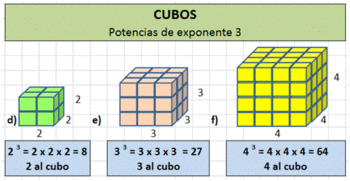
Cómo se leen las potencias:
Cuando el exponente es 2 se dice "elevado al cuadrado", cuando el exponente es 3 se dice "elevado al cubo". En los demás casos se dice "elevado a la cuarta, quinta, sexta... potencia".
Actividad para aprender a calcular potencias de números enteros.
Actividades sobre potencias de números enteros.
Signo de la potencia
Signo de la potencia
Dependiendo del signo de la base tenemos dos posibilidades:
- Base positiva: Al elevar un número positivo a una potencia, el resultado es positivo.
- Base negativa: Al elevar un número negativo a una potencia, el resultado es positivo si el exponente es par y negativo si es impar.
Cálculo de potencias cuya base es un número entero negativo. Ejemplos.
1) Completa la tabla. En ella debes indicar la base, el exponente, el valor y la cómo se leen las siguientes potencias de números enteros:
2) Escribe en forma de potencia:
- a)
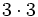
- b)
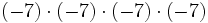
- c)
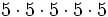
- d)
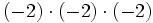
3) Escribe cómo se leen las siguientes potencias:
4) Escribe las siguientes potencias en forma de producto:
5) Escribe cada producto en forma de potencia, calcula su valor e indica cuál es la base y el exponente.
6) Calcula:
- a) Doce elevado al cuadrado.
- b) Once elevado al cubo.
- c) Tres elevado a la quinta.
- d) Dos elevado a la cuarta.
7) Desarrolla las siguientes potencias:
8) Calcula las siguientes potencias y razona cuánto valen todas las potencias de base 1:
- Actividad para aprender a calcular potencias de números enteros con base positiva o negativa.
- Actividad para practicar las potencias de enteros.
Calcula las siguientes potencias y comprueba los resultados en la escena siguiente:
a) ( − 3)4 b) ( − 4)5 c) ( − 10)5 d) ( − 2)10
Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Actividad sobre potencias cuya base es un número entero.
Ejercicios de autoevaluación en los que debes determinar el signo de la potencia cuya base es un número entero.
Ejercicios de autoevaluación de potencias cuya base es un número entero.
Ejercicios de autoevaluación de potencias cuya base es un número entero.
Ejercicios de autoevaluación de potencias cuya base es un número entero.
Propiedades de las potencias de enteros
Las potencias de números enteros cumplen las mismas propiedades que las potencias de números naturales.
Ver: Propiedades de las potencias de números naturales
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
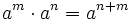
- 2. Cociente de potencias de la misma base:
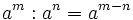
- 3. Potencia de un producto:
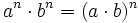
- 4. Potencia de un cociente:
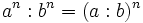
- 5. Potencia de otra potencia:
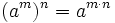
Propiedades de las potencias y ejemplos:
- Potencias de exponente 0.
- Potencias de exponente 1.
- Producto de potencias de la misma base.
- Cociente de potencias de la misma base.
Propiedades de las potencias y ejemplos:
- Potencia de otra potencia.
- Potencia de un producto.
- Potencia de un cociente.
Calcula:
- a)
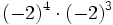 ; b)
; b) 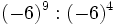
- c)
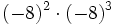 ; d)
; d) 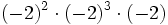
- e)
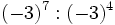 ; f)
; f) 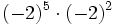
- g)
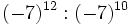 ; h)
; h) 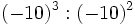
10) Escribe en forma de una sola potencia:
- a)
![[(-2)^3]^5\;](/wikipedia/images/math/8/8/6/886e30889b011f5f83334ec9296c0152.png) ; b)
; b) ![[(-3)^2]^3\;](/wikipedia/images/math/f/0/3/f037bb097909faad6873a0992df599fe.png)
- c)
![[(-5)^2]^4\;](/wikipedia/images/math/5/0/8/508d047dc4eb1a22b590a2f901a2fab9.png) ; d)
; d) ![[(-6)^3]^3\;](/wikipedia/images/math/4/c/8/4c8eef59c8fa17ac5bf2860de4ab42b4.png)
- e)
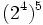 ; f)
; f) 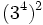
- g)
![[(-2)^1]^6\;](/wikipedia/images/math/d/f/3/df39089d6f5cc9c51e1d93713bb5f895.png) ; h)
; h) ![[(-2)^2]^6\;](/wikipedia/images/math/2/d/9/2d9edbe794a96dc0e0737db47be9067b.png)
- i)
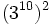 ; j)
; j) 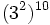
11) Expresa en forma de producto de varias potencias:
- a)
![[(-3) \cdot (-2) \cdot (-5)]^4\;](/wikipedia/images/math/3/2/6/3267df8521104f4db4a75cebb28001f7.png)
- b)
![[(-2) \cdot 5 \cdot (-6)]^2\;](/wikipedia/images/math/6/3/e/63e0b632e8c81875b6431d372a903f72.png)
- c)
![[2 \cdot 7 \cdot 6]^3\;](/wikipedia/images/math/1/a/0/1a083a19f18fa30e36b04f11289e2a1c.png)
- a)
![[(-2) \cdot (-3) \cdot (-6)]^3\;](/wikipedia/images/math/2/2/2/222cfc62f8027cac612dad7e3962dd04.png)
11) Expresa en forma de una sola potencia:
- a)
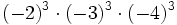
- b)
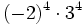
- c)
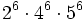
- d)
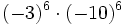
12) Calcula los cuadrados de los cinco primeros números positivos.
14) Escribe las cuartas potencias de: -3, -2, -5, 3, 2 y 5.
15) Calcula:
- a)
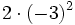 ; b)
; b) 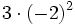
- c)
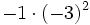 ; d)
; d) 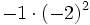
- e)
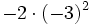 ; f)
; f) 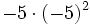
- g)
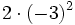
16) Escribe como potencias de base positiva:
17) Escribe el resultado como potencia de base positiva:
- a)
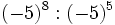 ; b)
; b) 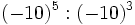
- c)
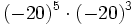 ; d)
; d) 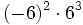
- e)
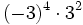 ; f)
; f) 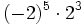
Simplifica: 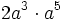
Simplifica: 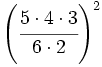
Simplifica: ![\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3](/wikipedia/images/math/7/1/b/71b5b62cb54ed835ba335fdbca4de909.png)
Simplifica: 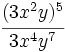
Simplifica: 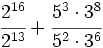
Actividades para aprender a calcular potencias de productos y cocientes.
Actividades para aprender a calcular productos y cocientes de potencias.
Actividades para aprender a calcular potencias de otra potencia.
Ejercicios resueltos sobre las propiedades de las potencias de números entero.
Actividades sobre las propiedades de las potencias de números enteros.
Ejercicios de autoevaluación sobre las propiedades de las potencias de números enteros.
Ejercicios de autoevaluación sobre las propiedades de las potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Raíces de números enteros
Sabemos que 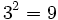 . Esta igualdad la podemos expresar de forma similar como
. Esta igualdad la podemos expresar de forma similar como 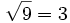 y se lee 3 es igual a la raíz cuadrada de 9.
y se lee 3 es igual a la raíz cuadrada de 9.
- Se define la raíz cuadrada de un número
 como otro número
como otro número  tal que
tal que 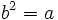 , que escribimos simbólicamente:
, que escribimos simbólicamente: 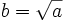 .
.
Dependiendo del signo del entero, su raíz puede existir o no. Tenemos los siguientes dos casos:
- La raíz cuadrada de un número entero positivo tiene dos soluciones iguales pero opuestas en signo, que no siempre son números enteros.
- La raíz cuadrada de un número entero negativo no existe.