Plantilla:Rectas y puntos notables en un triángulo

De Wikipedia

(Diferencia entre revisiones)
Revisión de 09:37 19 jul 2017
Coordinador (Discusión | contribuciones)

← Ir a diferencia anterior		 Revisión de 09:40 19 jul 2017
Coordinador (Discusión | contribuciones)

Ir a siguiente diferencia →
Línea 52: Línea 52:
}} }}
* '''Recta de Euler''' * '''Recta de Euler'''
-{{Tabla75|celda2=[[Imagen:recta_euler.png|center|250px]]|celda1={{p}}+{{Tabla75|celda2=[[Imagen:recta_euler.jpg|center|250px]]|celda1={{p}}
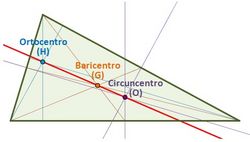
:La recta de Euler de un triángulo es aquella recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo :La recta de Euler de un triángulo es aquella recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo
{{p}} {{p}}

Revisión de 09:40 19 jul 2017

  • Medianas y baricentro

Las medianas de un triángulo son las rectas que unen cada vértice con el punto medio del lado opuesto.
Las tres medianas se cortan en un punto llamado baricentro y es el centro de gravedad del triángulo: desde este punto podríamos atarlo con un hilo y quedaría suspendido horizontalmente.

Medianas y baricentro (8´51")     Sinopsis:

Medianas y baricentro de un triángulo. Propiedad del baricentro.

Baricentro     Descripción:

En esta escena podrás ver e interactuar con un triángulo y ver su baricentro y sus medianas.

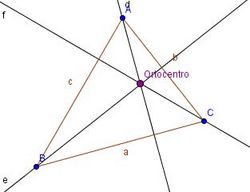
  • Alturas y ortocentro

Las alturas de un triángulo son las perpendiculares desde cada vértice al lado opuesto.
Las tres alturas de un triángulo se cortan en un punto llamado ortocentro (O).

Alturas y ortocentro (7´38")     Sinopsis:

Alturas y ortocentro de un triángulo según sea rectángulo, acutángulo u obtusángulo.

Ortocentro     Descripción:

En esta escena podrás ver e interactuar con un triángulo y ver su ortocentro y sus alturas.

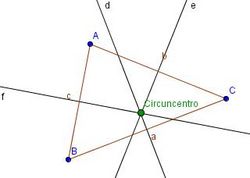
  • Mediatrices y circuncentro

Las mediatrices de un triángulo son las perpendiculares a los puntos medios de cada lado.
Las tres mediatrices siempre se cortan en un punto llamado circuncentro, que es el centro de la circunferencia circunscrita al triángulo, que pasa por los tres vértices del triángulo.

Circuncentro     Descripción:

En esta escena podrás ver e interactuar con un triángulo y ver su circuncentro y sus mediatrices.

  • Bisectrices e incentro

Las bisectrices de un triángulo son las rectas que dividen a sus ángulos en dos partes iguales.
Las tres bisectrices de un triángulo cualquiera se cortan en un punto llamado incentro, que es el centro de la circunferencia inscrita al triángulo, que es tangente a los tres lados del triángulo.

Incentro     Descripción:

En esta escena podrás ver e interactuar con un triángulo y ver su incentro y sus bisectrices.

  • Recta de Euler

La recta de Euler de un triángulo es aquella recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo

Recta de Euler     Descripción:

En esta escena podrás ver e interactuar con un triángulo y ver la recta de Euler.

Elementos notables de un triángulo     Descripción:

Actividades en las que podrás aprender cuáles son los puntos y rectas notables de un triángulo.

Elementos notables de un triángulo (5´44")     Sinopsis:

En este video vamos a estudiar las rectas y puntos notables de un triángulo:

  • Rectas: bisectriz, mediana, mediatriz y altura.
  • Puntos: incentro, baricentro, circuncentro y ortocentro.
Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Rectas_y_puntos_notables_en_un_tri%C3%A1ngulo"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda